上海市典型高層建筑結構基本自振周期測試與回歸分析

閆培雷， 孫柏濤

(中國地震局工程力學研究所 中國地震局地震工程與工程震動重點實驗室,哈爾濱 150080)

隨著經濟發展和社會進步，上海市高層建筑從20世紀80年代的121幢已經發展到如今的3萬余幢[1]，已成為上海市的主要建筑結構形式之一。上海市一旦遭受破壞性地震或強臺風，高層建筑的破壞將造成巨大的經濟損失和人員傷亡。高層建筑在風荷載和地震作用下產生振動和變形的大小取決于結構自身動力特性以及外部動力作用的特性。基本自振周期是十分重要的結構動力特性，其可用于反應譜法中估算結構承受的地震作用，計算結構的風壓脈動增大系數進而確定結構承受的風荷載，作為控制結構側移剛度的重要指標并從宏觀上判斷結構側移剛度是否合理[2]。

結構基本自振周期可通過理論計算和現場測試兩種方法得到。理論計算方法對結構的質量分布、材料實際性能、節點剛度以及施工質量進行了必要簡化，計算結果往往大于實際周期，導致采用理論計算周期得到的結構地震作用偏小。現場測試獲得的動力特性是建筑物建成后實際性態，其結果準確可靠[3-6]；對比實測周期與理論計算周期，可以驗證理論計算中簡化方法的合理性；通過對特定結構形式的建筑進行現場測試，歸納總結一定規律，得到其自振周期經驗公式，可用于快速估算該結構形式建筑的動力特性及其承受的地震作用[7-10]。

《建筑結構荷載規范》(GB50009—2012)[11]中有關高層建筑的基本自振周期經驗公式是基于北京、上海、天津、廣州、成都等十幾個城市內高度在50 m以下的160 余幢框架結構和80余幢剪力墻結構的實測數據擬合而成的[12]。近年來，上海市新建高層建筑的高度絕大多數都超過50 m，并且高層建筑的結構形式也不局限于框架結構和剪力墻結構，如將文獻[12]中的統計規律應用到上海市目前的高層建筑結構設計中，其合理性和精度尚存疑問。本文通過對上海市已建成的9幢典型高層建筑進行現場測試，獲得結構動力特性；給出以高寬比為自變量的結構基本自振周期經驗公式，供結構設計人員參考使用。本文給出的公式是對我國《建筑結構荷載規范》(GB50009—2012)[11]的補充和完善。

1 結構動力特性測試

1.1 測試結構概況

9幢高層建筑的統計信息如表1所示。結構用途以辦公和商業為主；框架-剪力墻結構平面內兩個主軸方向的尺寸相差較大，多呈“板式”，框架-核心筒結構平面內兩個主軸方向的尺寸接近，多呈“塔式”；結構剛度沿豎向變化基本均勻。

1.2 現場測試方案

1.2.1 測試方法

采用環境激勵法(亦稱脈動法)對結構進行動力特性測試。環境激勵法利用結構對自然環境下微弱干擾的脈動響應來確定其動力特性。環境激勵法不采用外部激振設備，對結構無損傷，不影響結構正常使用，在自然環境條件下即可測定結構動力特性。

1.2.2 測試方案

在現場測試前，搜集結構施工圖并查找結構高度、長度和寬度等信息，依據結構平面圖計算確定結構平面剛度中心和質量中心。

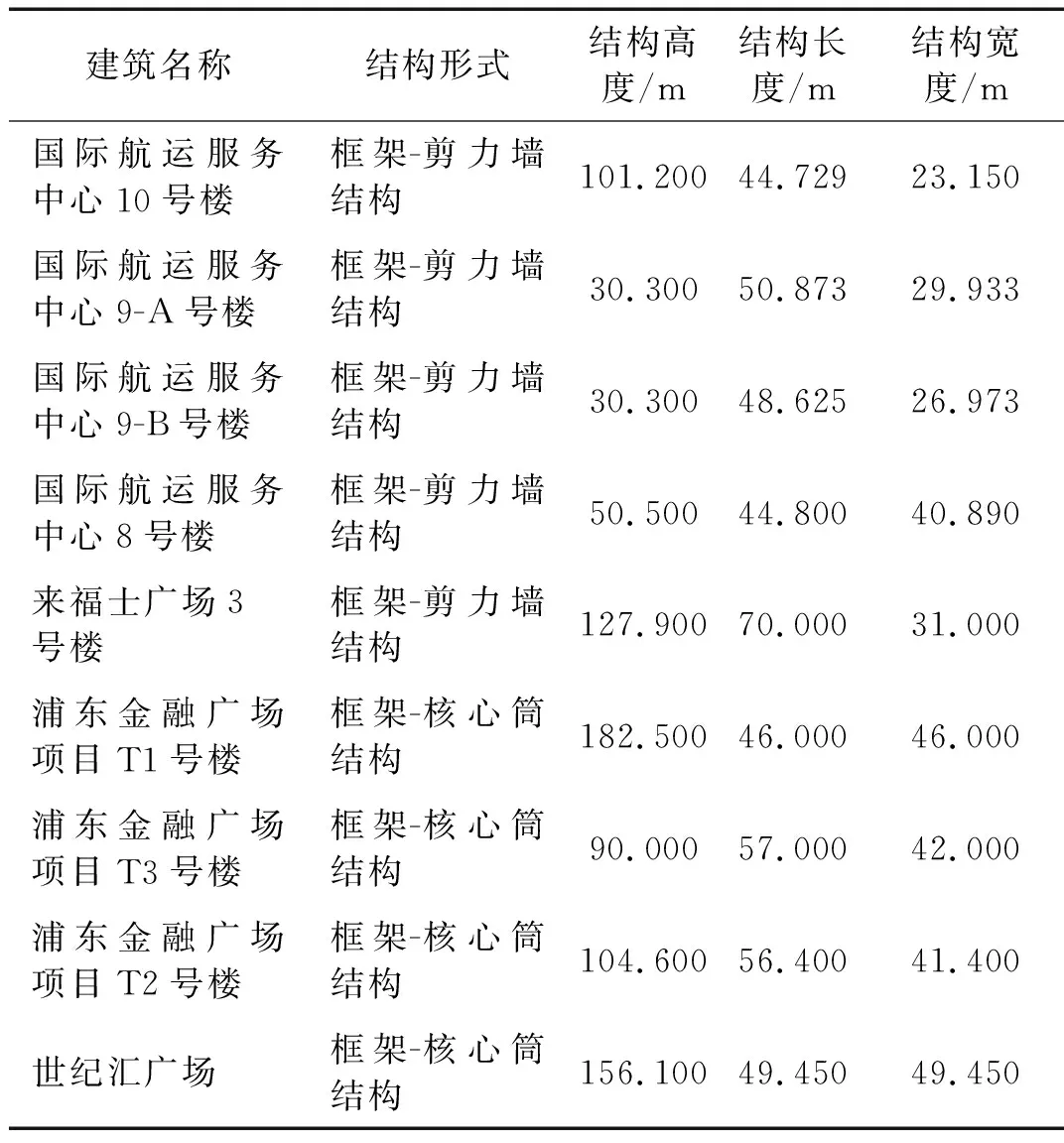
表1 建筑物的基本信息

每棟結構均設置兩個測試點，分別位于頂層剛度中心和總高度一半處樓層的剛度中心；每個測點分別測試3次，每次測試的振動響應(速度)數據包含1條水平縱向數據和1條水平橫向數據。

1.2.3 儀器及布置

儀器采用中國地震局工程力學研究所研發的G01NET-2通用數據采集器和941-B超低頻測振儀。G01NET-2是多通道數據同步高速采集儀(如圖1)，主要應用于結構測試中振動信號的采集、分析及處理，其性能在國內處于先進水平。941-B型超低頻測振儀是一種用于超低頻或低頻振動測量的多功能儀器(如圖2)，主要用于地面和結構物的脈動測量，儀器具有體積小、重量輕、使用方便、分辨率高、動態范圍大等特點。

圖1 G01NET-2通用數據采集器

941-B型超低頻測振儀的布置原則如下：

(1) 在結構平面內，941-B超低頻測振儀盡可能安放在結構的剛度中心處，并按結構水平縱橫雙向布置，保證測振儀接收到的信號突出平動信號，扭轉振動信號盡可能小；

圖2 941-B超低頻測振儀

(2) 在結構的豎向上，由于結構速度幅值隨層數的增加而增大，因而在結構頂層及結構總高度一半處的樓層布置布置941-B超低頻測振儀，即可獲得可靠準確的數據，不必層層布置測振儀。

1.2.4 數據采集

現場測試時，單次數據采樣時間為5 min，采樣頻率為50 Hz；環境激勵包含的頻譜非常豐富，可近似為有限帶寬白噪聲，在保證單次測試時間長度一定的前提下，即可用結構脈動響應的單個樣本函數來描述隨機過程的所有特征，并明顯反映出結構的動力特性。

2 測試數據及處理

2.1 數據處理

將采集得到速度時程數據經過快速傅里葉變換(FFT)得到結構脈動響應功率譜[13-14]，采用峰值法識別結構的基本自振周期，而后將6組結果取平均值，最終獲得結構在水平縱橫兩個方向上的基本自振周期，9幢高層建筑的水平縱橫兩個方向的基本自振周期結果如表2所示。以上海市黃浦區的來福士廣場3號樓為例(如圖3和圖4)，現場測試數據如圖5，數據處理結果如圖6。

圖3 來福士廣場3號樓

圖4 結構頂層動力性能測試

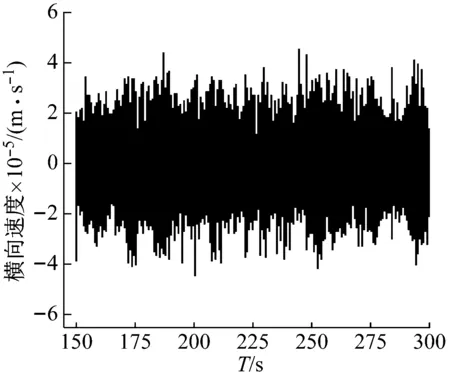
圖5 水平橫向速度時程數據

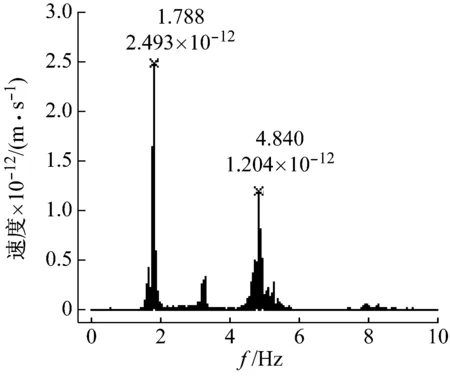
圖6 水平橫向功率譜

2.2 測試結果

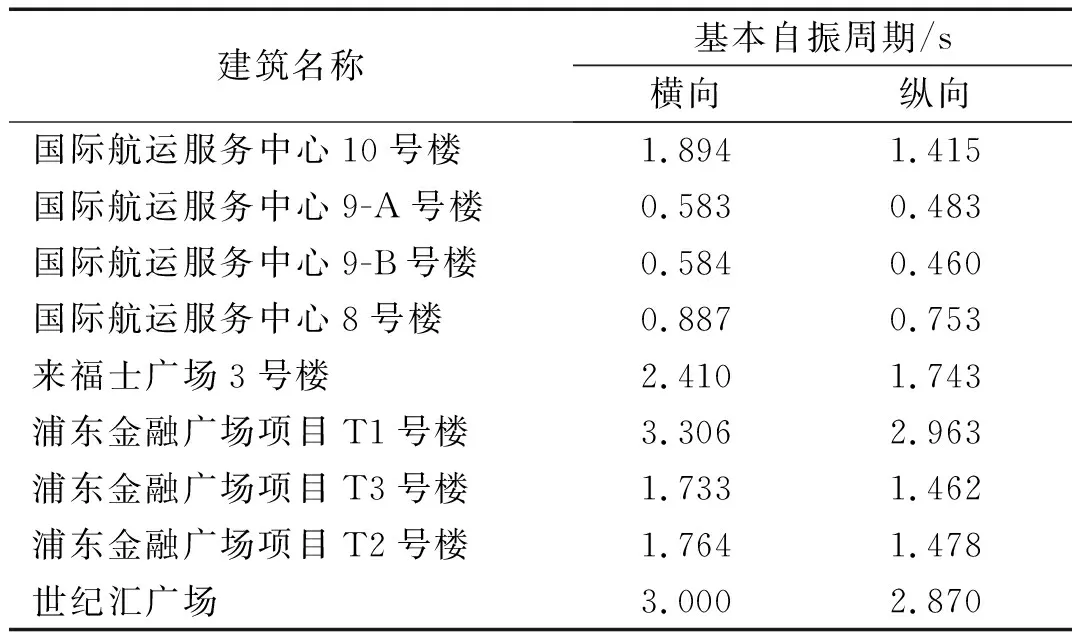
表2 結構測試結果匯總

3 框架-剪力墻結構的基本自振周期經驗公式

《建筑結構荷載規范》(GB50009—2012)[11]中給出的鋼筋混凝土框架結構和框架-剪力墻結構的基本自振周期經驗公式如下所示：

(1)

依據式(1)對測試的5幢框架-剪力墻結構的基本自振周期進行了計算，并與實測結果進行了對比，結果如表3所示，表3中的誤差定義為：

(2)

表3 測試結構自振周期與經驗公式對比

Tab.3 Comparison between fundamental vibration period acquired and that calculated by empirical formula

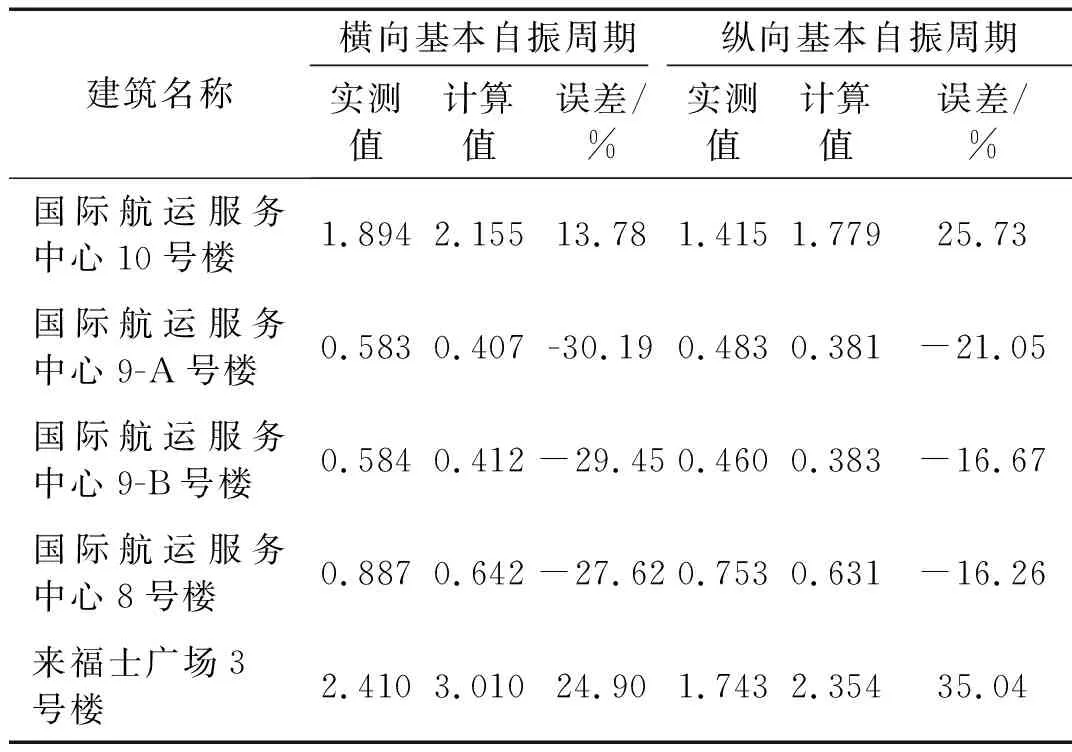
建筑名稱橫向基本自振周期縱向基本自振周期實測值計算值誤差/%實測值計算值誤差/%國際航運服務中心10號樓1.894 2.155 13.78 1.415 1.779 25.73 國際航運服務中心9-A號樓0.583 0.407 -30.19 0.483 0.381 -21.05 國際航運服務中心9-B號樓0.584 0.412 -29.45 0.460 0.383 -16.67 國際航運服務中心8號樓0.887 0.642 -27.62 0.753 0.631 -16.26 來福士廣場3號樓2.410 3.010 24.90 1.743 2.354 35.04

從表3看出，實測值與式(1)的計算值存在較大誤差，其中國際航運服務中心10號樓和來福士廣場3號樓為辦公樓且高度均超過100 m，為保證結構具有足夠側向剛度和使用功能，平面內布置了較多的鋼筋混凝土剪力墻和隔墻，導致結構實測值較計算值小，誤差為正；其它3幢結構平面內僅布置了少量的鋼筋混凝土剪力墻，且較為空曠，結構整體側向剛度較弱，導致結構實測值較計算值大，誤差為負。因此，判斷式(1)對高度超過50 m的框架-剪力墻結構不適用。

環境激勵法實測的基本自振周期是結構在微小變形下的性能參數；抗震設計所需的是結構在地震中發生足夠強的振動但不進入非線性反應時的基本自振周期，該值大于環境激勵法實測的基本自振周期。因此，需將環境激勵法實測的基本自振周期乘以修正系數。針對鋼筋混凝土框架結構和框架-剪力墻結構，依據王廣軍等[15]研究，修正系數取1.15。

參考式(1)的形式，同時考慮測試結構平面形狀以“板式”為主，對結構基本自振周期和高寬比采用SPSS22.0統計分析軟件在水平縱橫兩個方向分別進行回歸分析，其結果如圖7和圖8所示。

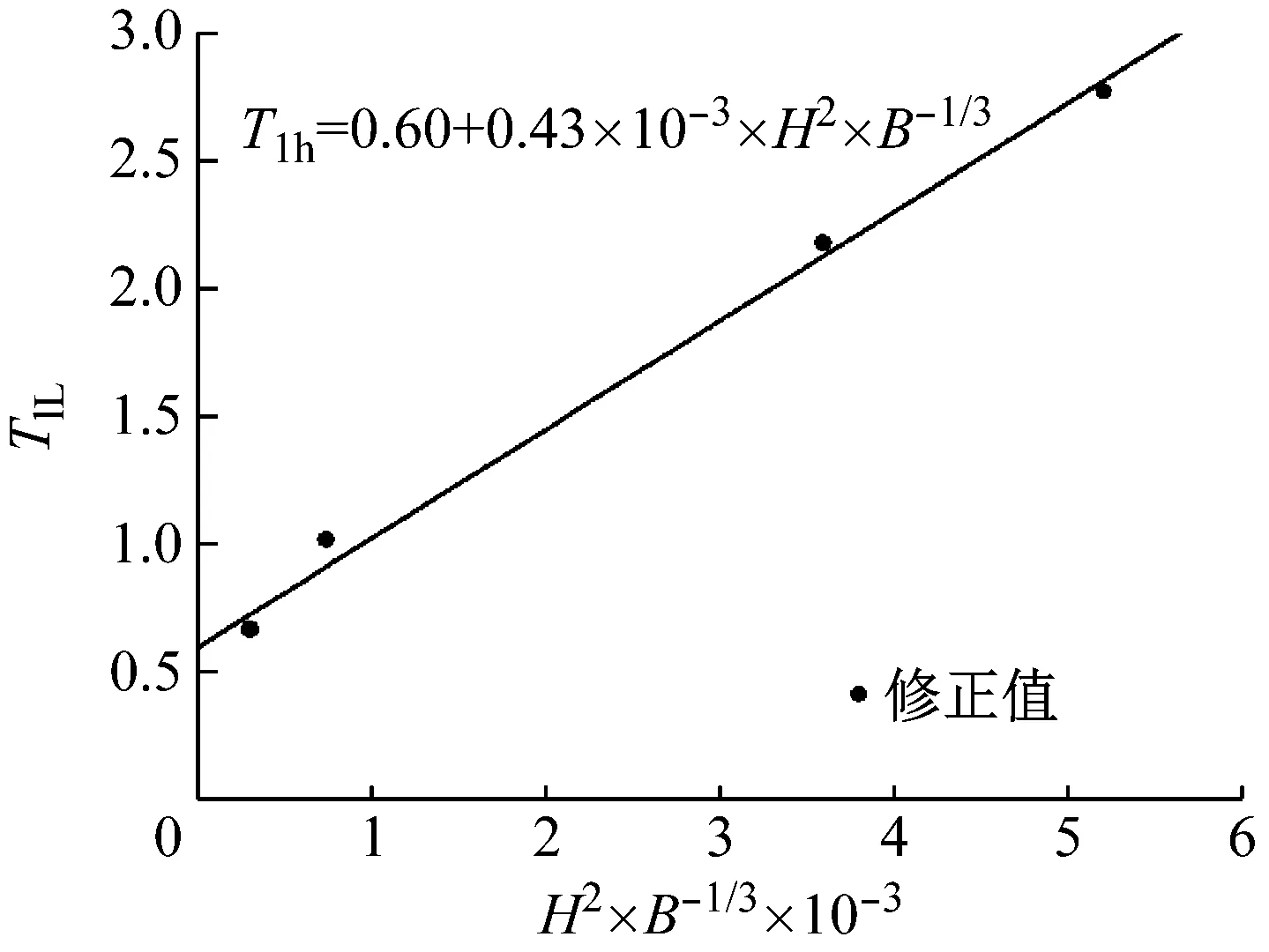
圖7 水平橫向上的基本自振周期經驗公式

Fig.7 Empirical formula of fundamental vibration period in the horizontal direction

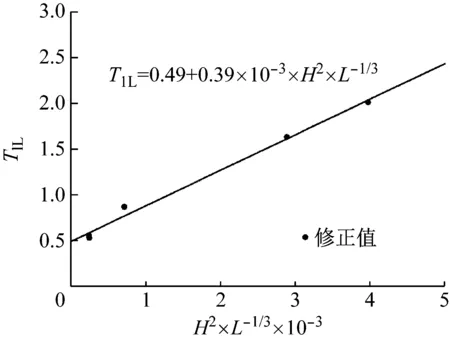
圖8 水平縱向上的基本自振周期經驗公式

Fig.8 Empirical formula of fundamental vibration period in the longitudinal direction

(3)

式中：T1h為結構水平橫向基本自振周期；H為結構高度；B為結構寬度。

該方程的歸回分析的決定系數R2=0.994。

(4)

式中：T1l為結構水平縱向基本自振周期；L為結構長度。

該方程的歸回分析的決定系數R2=0.992。

擬合結果顯示，所得公式的決定系數非常高，說明高層鋼筋混凝土框架-剪力墻結構的基本周期與結構高寬比有顯著的關系，基本自振周期隨著高度的增加而增大。

選擇文獻[16]中的鋼筋混凝土框架-剪力墻結構用于驗證式(3)和式(4)的可靠性。該結構的高度為49.5 m，寬度為22.7 m，長度為91.6 m。從表4可以看出,公式誤差率控制在17%之內，該精度在結構初始設計階段能夠滿足快速估算結構承受水平地震作用和風荷載的需求。

表4 測試結構自振周期與式(3)、(4)對比

Tab.4 Comparison between fundamental vibration period acquired and that calculated by formula (3) and (4)

橫向縱向實測值/s式(3)值/s誤差/%實測值/s式(4)值/s誤差/%0.7250.63712.10.6040.70216.2

4 框架-核心筒結構的基本自振周期經驗公式

針對框架-核心筒結構，依據方鄂華等[17]研究，修正系數取1.20。參考式(1)的形式，考慮測試結構平面形狀以“塔式”為主且兩個主軸方向實測數據存在顯著差異，對結構基本自振周期和高寬比采用SPSS22.0統計分析軟件在水平縱橫兩個方向分別進行回歸分析，其結果如圖9和圖10所示。

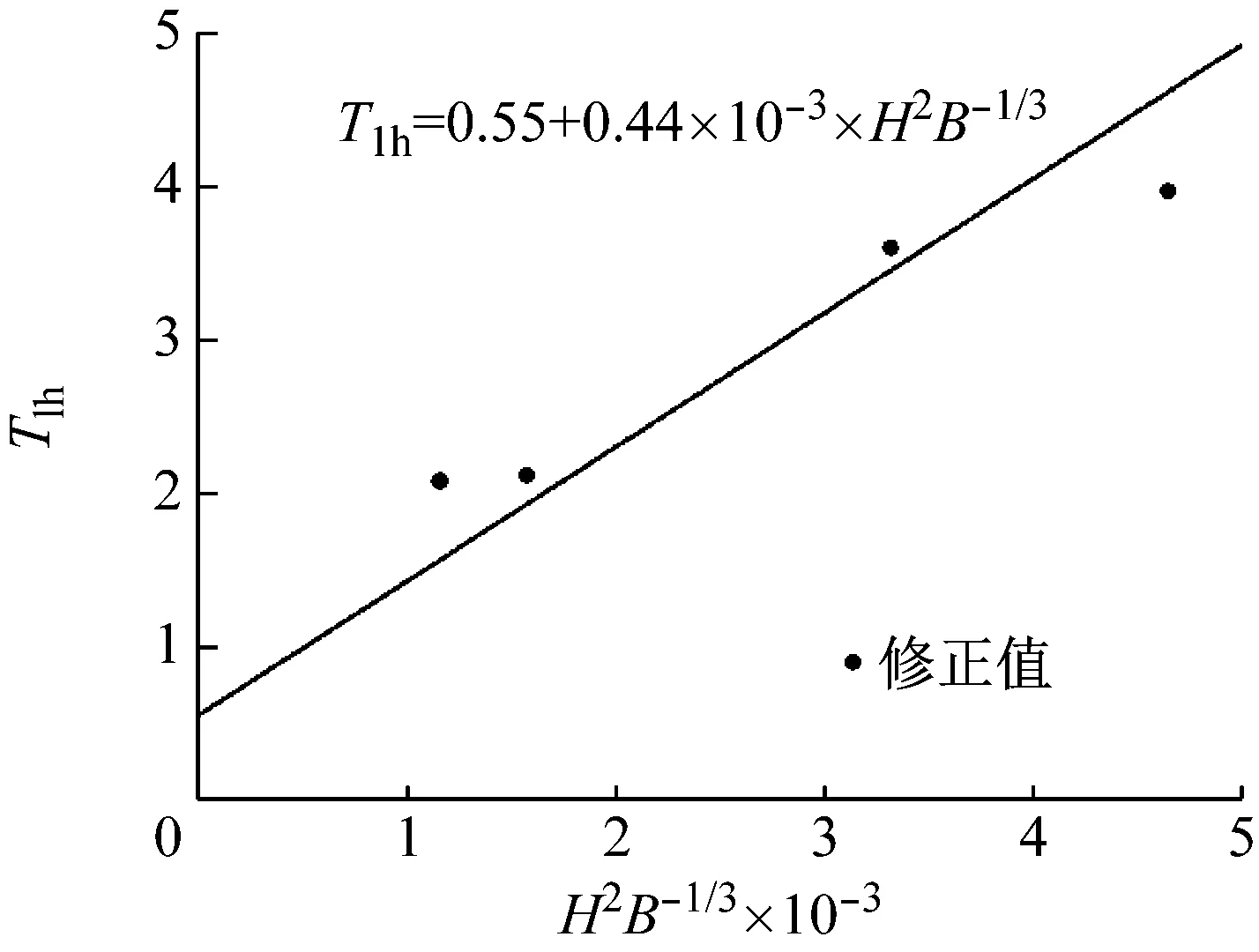
圖9 水平橫向上的基本自振周期經驗公式

Fig.9 Empirical formula of fundamental vibration period in the horizontal direction

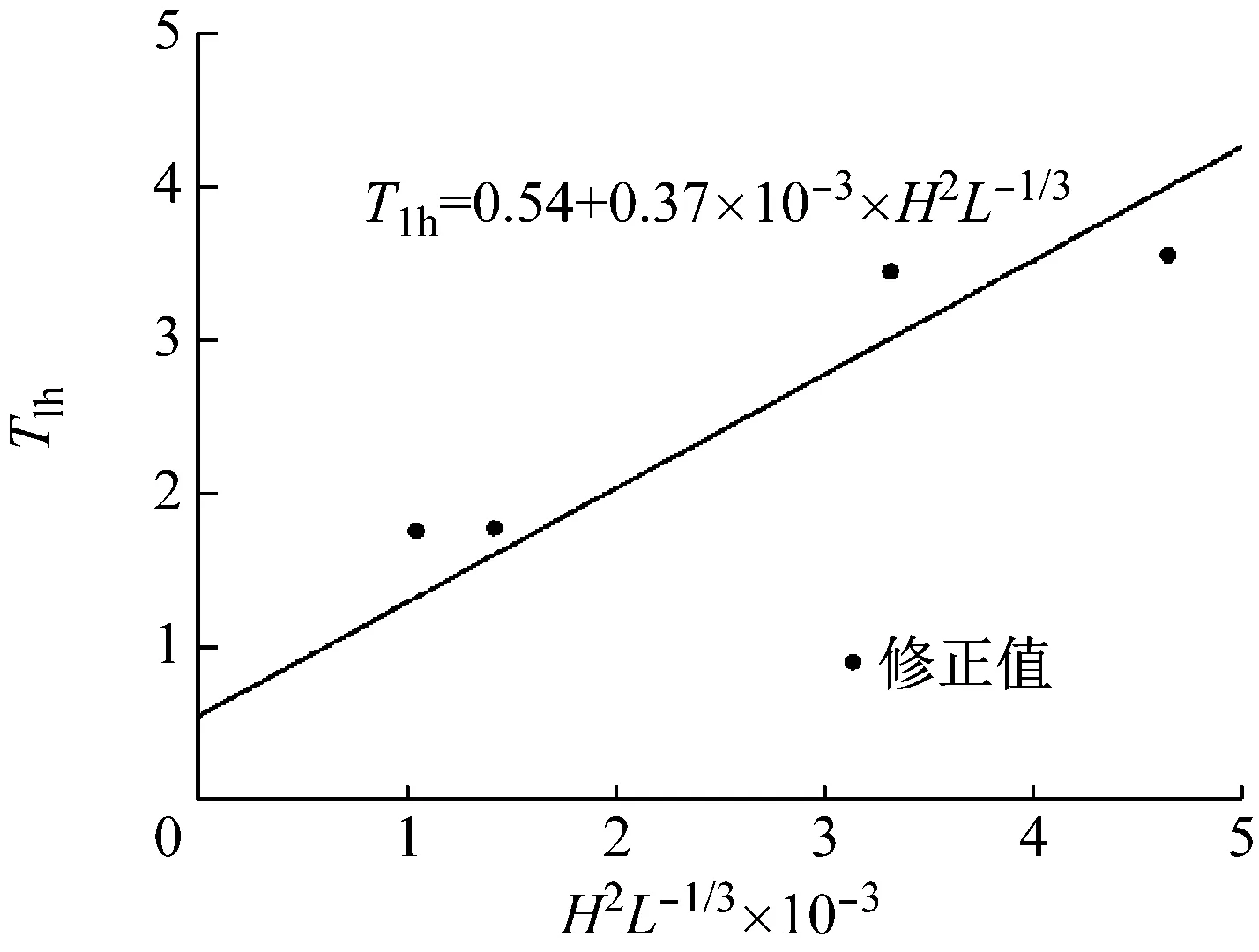
圖10 水平縱向上的基本自振周期經驗公式

Fig.10 Empirical formula of fundamental vibration period in the longitudinal direction

(5)

該方程的歸回分析的決定系數R2=0.956。

(6)

該方程的歸回分析的決定系數R2=0.915。

擬合結果顯示，所得公式的決定系數非常高，說明高層框架-核心筒結構的基本周期與結構高寬比有顯著的關系，基本自振周期隨著高度的增加而增大。

選擇文獻[18]中的鋼筋混凝土框架-核心筒結構用于驗證式(5)和式(6)的可靠性。該結構的高度為141 m，寬度為41.5 m，長度為44 m。從表5可以看出,公式誤差率控制在30%之內，該精度在結構初始設計階段能夠滿足快速估算結構承受水平地震作用和風荷載的需求。

表5 測試結構自振周期與式(5)、(6)對比

Tab.5 Comparison between fundamental vibration period acquired and that calculated by formula (5) and (6)

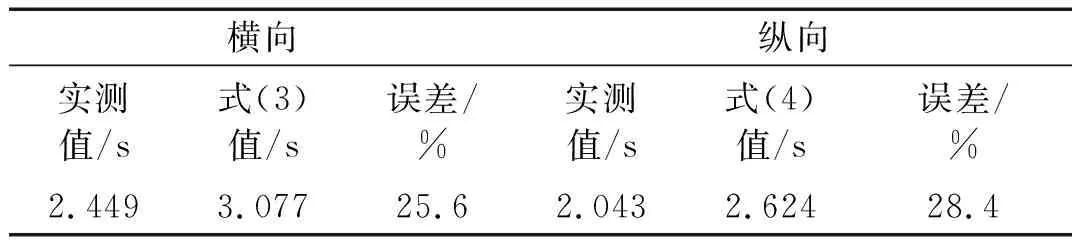
橫向縱向實測值/s式(3)值/s誤差/%實測值/s式(4)值/s誤差/%2.4493.07725.62.0432.62428.4

5 結 論

基于上海市9幢典型高層建筑的動力性能現場測試數據，識別了結構在水平縱橫兩個方向上的基本自振周期并進行了統計分析，得到了結構在水平縱橫兩個方向上的基于結構高寬比的基本自振周期經驗公式。主要結論如下：

(1) 給出了高度在30～130 m之間的結構在水平縱橫兩個方向上基本自振周期經驗公式，對實測結構的誤差為17%之內，該公式是對現行規范中結構基本自振周期經驗公式相關規定的補充和完善；

(2) 首次給出了高度在90～190 m之間高層框架-核心筒結構在水平縱橫兩個方向上基本自振周期經驗公式，對實測結構的誤差為30%之內；

(3) 在高層建筑的初始設計階段，可以利用本文擬合的公式，基于結構的總高度、長度和寬度，估算結構的基本自振周期，進而利用反應譜法快速估算結構承受的地震作用以及確定風荷載，最終基于上述分析控制整體結構設計。