三角函數(shù)中數(shù)與形手牽手
吳 娟
(江蘇省昆山中學(xué) 215300)
普通高中數(shù)學(xué)學(xué)科核心素養(yǎng)之一是直觀想象,直觀想象是指借助幾何直觀感知實物的形態(tài)與變化,利用圖形理解和解決數(shù)學(xué)問題的過程.華羅庚先生曾指出“數(shù)缺形時少直觀,形少數(shù)時難入微;數(shù)形結(jié)合百般好,隔裂分家萬事非.”數(shù)形結(jié)合思想是高中數(shù)學(xué)重要的思想方法.本文主要就數(shù)形結(jié)合思想在三角函數(shù)學(xué)習(xí)中的應(yīng)用與大家一起探討.
一、數(shù)形結(jié)合概念
1.數(shù)形結(jié)合思想
數(shù)學(xué)中,數(shù)與形是兩個最主要的研究對象.“數(shù)形結(jié)合”思想是把數(shù)或數(shù)量關(guān)系與圖形對應(yīng)起來,借助圖形來研究數(shù)量關(guān)系或者利用數(shù)量關(guān)系研究圖形的性質(zhì).它們在內(nèi)容上相互聯(lián)系,方法上相互滲透,在一定條件下可以相互轉(zhuǎn)化.恩格斯是這樣定義數(shù)學(xué)的:“數(shù)學(xué)是研究現(xiàn)實世界的量的關(guān)系與空間形式的科學(xué).”這就意味著數(shù)形結(jié)合是數(shù)學(xué)的本質(zhì)特征,宇宙間的萬事萬物是數(shù)與形和諧的統(tǒng)一,因此數(shù)形結(jié)合思想是數(shù)學(xué)的精髓與靈魂.
數(shù)形結(jié)合是研究數(shù)學(xué)問題并解決問題的模型轉(zhuǎn)化的一種基本思想與基本方法.它能溝通數(shù)與形的內(nèi)在聯(lián)系.具體來說就是在研究問題的過程中既分析其代數(shù)含義,又揭示其幾何意義,使數(shù)量關(guān)系和幾何形式巧妙、和諧的結(jié)合起來,充分利用這種結(jié)合,尋找解決問題的思路,使抽象問題直觀化,復(fù)雜問題簡單化,從而使問題得以解決的一種重要的數(shù)學(xué)思想.
2.數(shù)形結(jié)合的價值
數(shù)形結(jié)合思想是中學(xué)數(shù)學(xué)重要的思想方法之一,在高中的數(shù)學(xué)學(xué)習(xí)中發(fā)揮著重要的作用.
首先,學(xué)生巧妙應(yīng)用數(shù)形結(jié)合思想能掌握到更多的知識點,也能使學(xué)生對整體的知識點進(jìn)行把控,形成良好的知識脈絡(luò),將各類知識點融會貫通;并且也能有效改善學(xué)生的思維能力和解題思路,為他們提供更多的學(xué)習(xí)方法和解題思路,也能為學(xué)生提供更多的學(xué)習(xí)認(rèn)知規(guī)律.
其次,正確的運用數(shù)學(xué)結(jié)合思想,能有效地培養(yǎng)學(xué)生的數(shù)學(xué)思維能力,豐富學(xué)生的思維方式.有利于對學(xué)生思維、興趣的培養(yǎng),從而不僅可以減輕學(xué)生的負(fù)擔(dān),也能給學(xué)生創(chuàng)造更好的學(xué)習(xí)思維方式.
再次,學(xué)會怎樣運用數(shù)形結(jié)合思想,也能幫助學(xué)生在學(xué)習(xí)中樹立良好的學(xué)習(xí)思想和學(xué)習(xí)習(xí)慣.可以幫助學(xué)生從多角度多層次思考問題,形成良好的思維方式;教導(dǎo)學(xué)生學(xué)會將抽象的問題具體化,更準(zhǔn)確地把握問題本身;可以鍛煉學(xué)生的思維模式,也能鍛煉他們的創(chuàng)造能力的思維發(fā)展.
二、數(shù)形結(jié)合思想在三角函數(shù)中的應(yīng)用
“依性作圖,以圖識性”是數(shù)形結(jié)合思想的重要體現(xiàn).三角函數(shù)在本質(zhì)上是對單位圓圓周上一點運動的“動態(tài)描述”,它的種種性質(zhì)和公式都是和單位圓的幾何性質(zhì)密切關(guān)聯(lián)的,這就要求在解決三角函數(shù)的相關(guān)問題上,應(yīng)巧妙地運用單位圓中的三角函數(shù)線和三角函數(shù)圖形,以形助數(shù),數(shù)形結(jié)合.數(shù)形結(jié)合貫穿了三角函數(shù)的整個章節(jié),三角函數(shù)在單位圓中的定義得出了三角函數(shù)線、三角函數(shù)的圖象、圖象的變化等都需要圖象的支持.
1.利用數(shù)形結(jié)合,有利于學(xué)習(xí)難點化解
在推導(dǎo)三角函數(shù)的誘導(dǎo)公式時,教科書上是從代數(shù)(三角函數(shù)的坐標(biāo)定義)的角度推導(dǎo)的,我們也可以利用三角函數(shù)的幾何表示(三角函數(shù)線)來推導(dǎo).單位圓中的三角函數(shù)線可以使抽象問題直觀化、生動化,變抽象思維為形象思維,有助于把握數(shù)學(xué)問題的本質(zhì),它是數(shù)學(xué)的規(guī)律性和靈活性的有機(jī)結(jié)合,也為學(xué)生的學(xué)習(xí)提供更廣闊的思維空間.
片段一:終邊相同的角的同一三角函數(shù)值相等.
如圖1,P是半徑為1的圓O上一點,點P的運動可以形象的描述為“周而復(fù)始”.當(dāng)點P旋轉(zhuǎn)一周時又回到了原來的地點,由三角函數(shù)線可知終邊相同的角的同一三角函數(shù)值相等.
片段二:如果角α的終邊與角β的終邊關(guān)于x軸對稱.
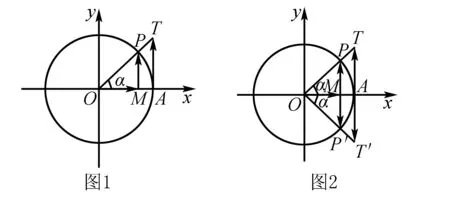
如圖2,設(shè)角α、β的終邊分別與單位圓交于P、P′,分別與x=1交于T,T′,由三角函數(shù)線可知sinα=MP,cosα=OM,tanα=AT;sinβ=MP′,cosβ=OM,tanβ=AT′;即:sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα.
當(dāng)角α的終邊與角β的終邊關(guān)于y軸、原點對稱,學(xué)生類比以上方法很快得出一系列的誘導(dǎo)公式.
在圖示中,先取α為銳角,關(guān)于x軸對稱,作出-α;關(guān)于y軸對稱,作出π-α;關(guān)于原點對稱,作出π+α,利用三角函數(shù)線很容易得出書上的誘導(dǎo)公式.但當(dāng)α不是銳角時,這些結(jié)論依然成立嗎?我們可以用坐標(biāo)即三角的代數(shù)定義來嚴(yán)格證明.
在這學(xué)習(xí)的過程中利用三角函數(shù)線的推導(dǎo)體現(xiàn)了圖形的直觀性,學(xué)生很容易接受;再用坐標(biāo)的代數(shù)證明又體現(xiàn)了數(shù)學(xué)的嚴(yán)謹(jǐn)性.學(xué)生掌握了誘導(dǎo)公式的本質(zhì),了解公式的來龍去脈,在理解中記憶,方能掌握得更扎實、更透徹,也為學(xué)生的學(xué)習(xí)提供更廣闊的思維空間.
2.利用數(shù)形結(jié)合,拓展解題思路
學(xué)生甲:作差
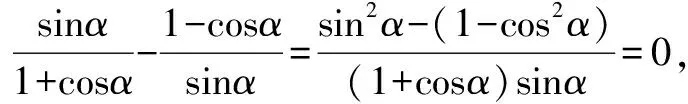
學(xué)生乙:觀察對角關(guān)系
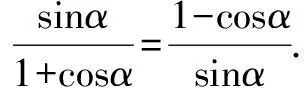
教師:還有其他想法嗎?這個式子能用圖形來解釋嗎?
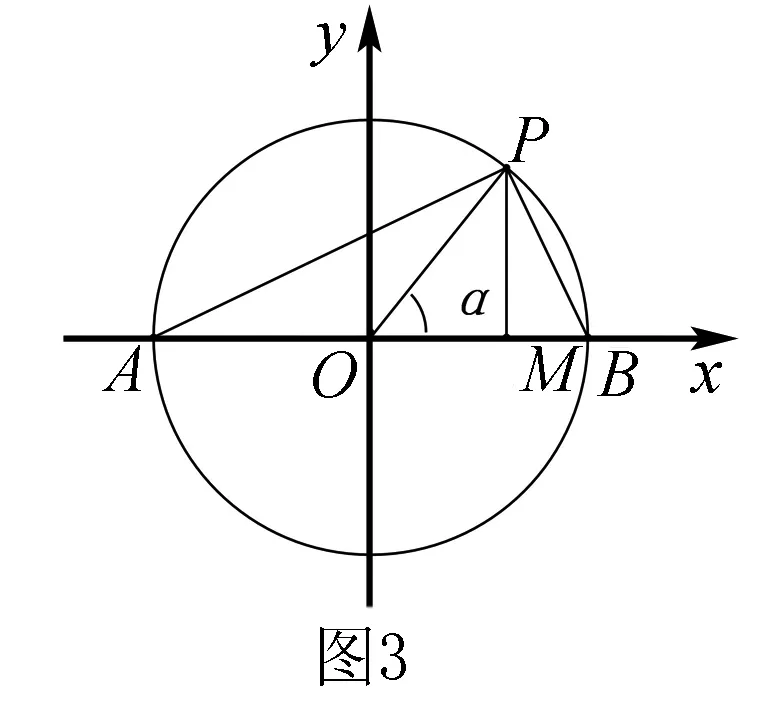
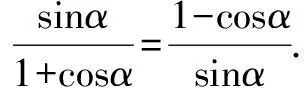
本題的數(shù)形結(jié)合揭示了三角函數(shù)在單位圓中的定義的本質(zhì)特征,在具體的教學(xué)過程中,引導(dǎo)學(xué)生主動地探索、發(fā)現(xiàn)、領(lǐng)會其中的聯(lián)系.數(shù)學(xué)知識與圖形有著密切的聯(lián)系,以具體的數(shù)學(xué)知識為載體、潛移默化地將數(shù)形結(jié)合的思想不斷滲透,隨著數(shù)形結(jié)合的思想不斷體現(xiàn),學(xué)生認(rèn)知也會不斷發(fā)展和逐漸深化,同時不斷提升學(xué)生的創(chuàng)新意識和創(chuàng)新能力.
片段四 若α為銳角(單位為弧度),試?yán)脝挝粓A及三角函數(shù)線,比較α,sinα,tanα之間的大小關(guān)系.
生甲:畫單位圓,利用三角函數(shù)線,可以得到sinα 教師:本題的難點在于α的轉(zhuǎn)化,我們怎么把α轉(zhuǎn)化出來 呢? 教師:弧AP是曲線,怎么比較大小呢?我們該如何利用圖形證明? 生丙:因為S△AOP 學(xué)生們都鼓起了掌,覺得非常的巧妙. 教師:非常好,本題的難點就在于要把α轉(zhuǎn)化,先把α轉(zhuǎn)化成弧長,再利用三角形和扇形的面積大小得出結(jié)論,所以圖形在三角中也起著非常重要的作用,數(shù)與形的結(jié)合使抽象的問題具體化,形象化,學(xué)生很樂意的接受了. 在教學(xué)過程中我們既要關(guān)注數(shù)學(xué)知識,更要揭示和顯化蘊(yùn)含在其中的數(shù)學(xué)思想方法,這樣數(shù)學(xué)知識不再是孤立的、零散的,而是具有了一定的聯(lián)系性、整體性與靈活性;我們不僅傳授數(shù)學(xué)知識,更要展示數(shù)學(xué)思維的美妙,引導(dǎo)學(xué)生體驗數(shù)學(xué)探索的過程.數(shù)學(xué)知識是數(shù)學(xué)思想方法的重要載體,數(shù)形結(jié)合思想方法在以上習(xí)題中的應(yīng)用開闊了學(xué)生分析問題的視野,拓展了學(xué)生的思維、提升了學(xué)生轉(zhuǎn)化問題解決問題的能力. “數(shù)”與“形”的轉(zhuǎn)化與結(jié)合不僅是一種重要的解題方法與策略,更是一種重要的數(shù)學(xué)思維與思想方法.首先需要的是一種意識:敏銳捕捉信息,恰當(dāng)?shù)臅r候建立適當(dāng)?shù)穆?lián)系;其次是一種轉(zhuǎn)化思想:根據(jù)數(shù)的結(jié)構(gòu)特征,構(gòu)造出與之相應(yīng)的圖形,并利用圖形的性質(zhì)和規(guī)律解決“數(shù)”的問題;再次是一種能力、一種思考的方式.在教學(xué)的過程中,讓學(xué)生了解數(shù)形結(jié)合思想產(chǎn)生的背景,把握數(shù)形結(jié)合思想的本質(zhì),感受數(shù)形結(jié)合思想的價值,形成良好的數(shù)學(xué)意識與數(shù)學(xué)思想.數(shù)與形相輔相成,和諧統(tǒng)一,完美結(jié)合,讓我們一同感受與體會數(shù)學(xué)之美,“數(shù)”與“形”牽手之妙.

