橢圓標準方程教學中傳統文化的滲透

摘要：職校學生亟待進行文化自信的培育，數學教育當仁不讓地肩負著文化傳承的義務。在進行橢圓標準方程教學時，從創新教學設計，發掘傳統文化內涵，優化教學實施過程，喚醒傳統文化基因，挖掘隱性資源，感悟傳統文化核心價值觀出發，在數學教育中進行傳統文化的滲透。

關鍵詞：橢圓;標準方程;傳統文化

中圖分類號：G712 文獻標志碼：A 文章編號：1673-9094-（2019）06C-0026-03

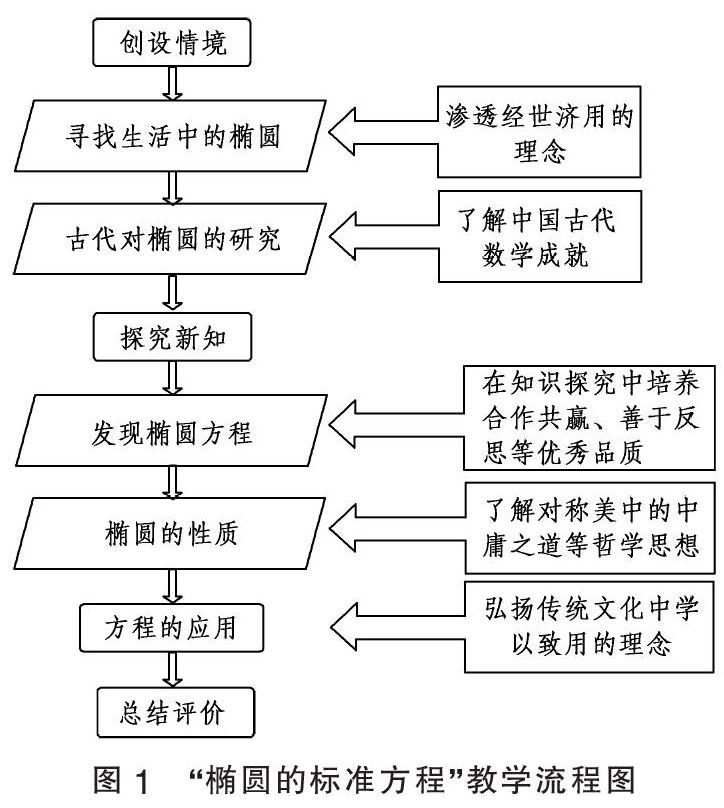
人文底蘊、責任擔當和科學精神是中國學生發展核心素養的重要內容。職校學生作為未來國家建設的生力軍，亟待進行文化自信的培育。作為中職階段重要文化基礎課程之一的數學，當仁不讓地肩負著文化傳承的使命。橢圓教學作為中職數學教學重要組成部分，有豐富的傳統文化資源可供探究。下面以橢圓的標準方程為例（見圖1），探究在數學教學過程中滲透傳統文化的路徑與方法。

一、 創新教學設計，發掘傳統文化內涵

（一）創新問題情境，注重數學社會屬性

中國古代數學最重要的特點之一是具有鮮明的社會性，強調數學知識在實際中的應用，這和我們今天的職業教育的基本理念是相通的。在中國歷史上，橢圓有“陶丘形”“圭竇形”等描述。在《郝懿行義疏》中解釋陶丘形為瓦器疊加在一起的樣子，唐代李賢把它比作“形如累兩盂也”。至于圭竇形，就是形狀如圭的墻洞（東漢鄭玄）。由此可見，中國古代對橢圓的認識主要來源于生產生活實踐，教師在進行橢圓的教學設計時，也要秉承這種理念。因此，橢圓教學的情境創設必須從生產生活實際出發，從解決實際問題出發。比如從圓球的陰影、傾斜杯中的水面等日常體驗中，使學生獲得對橢圓的初步感知。

中國古代數學具有輝煌的成就，集中國古代數學大成的《算經十書》等著作的內容，幾乎都反映了當時社會生產與經濟文化等方面的某些實際需求，具有很強的實用性。這些典籍既是中國傳統文化傳承的載體，也為當代數學教師的教學提供了豐富的文化資源。

（二）創新學習重點突破途徑，寓理于算

橢圓標準方程的推導是橢圓教學的重點之一，這個推導過程涉及大量的運算，包括了移項、平方、合并同類項以及換元等計算技巧。西方數學的長處在于推理演繹，而中國古代數學則在計算方法上獨樹一幟。運算的目的是為了尋找解決問題的方法，在尋找方法的過程中自然蘊藏著推理論證，運算與推理在本質上是互通的，這就是中國傳統文化中的“寓理于算”。教師在引導學生推導橢圓標準方程的運算過程中，不僅要通過算理算法促進學生數學思維能力的提升，還要讓學生意識到這個運算方法是可以擴展遷移的，這就可以為后續的雙曲線、拋物線的學習奠定基礎。

（三）創新定義內涵解構，取長補短

當前的數學教材一般對橢圓采用如下定義：動點到兩個定點的距離之和（此和大于兩定點距離）為定值的點的軌跡為橢圓，也稱作橢圓的第一定義。這個定義不僅能讓學生通過“以繩畫圓”繪制出橢圓圖形，也能夠比較容易地建立直角坐標系推導出橢圓的標準方程。據統計，世界上有65%的教材使用這個定義。相比較而言，中國古代對橢圓的定義則是以定性形式出現，先后有斜圓、瘦圓等定義，最后這些定義統一為“橢者，長圓也”（《辭海》）。觀察這些定義就會發現，橢圓和圓具有密切關系。教師可以從橢圓的漢語內涵出發，引導學生尋找橢圓與圓的聯系。事實上，對于橢圓標準方? 來說，當長軸與短軸相等時，橢圓方程就質變為圓的方程x2+b2=a2。這樣不僅讓學生理解了同為圓錐曲線的橢圓和圓的內在聯系，還能讓學生體會極限的數學思想以及量變引起質變的哲學思想。漢語詞根的單音節特點，使得它的構詞的邏輯性極強。在職校教學中有時對數學術語“望文生義”，也能取得意想不到的效果。

二、優化教學實施過程，喚醒傳統文化基因

中國傳統文化中許多教育思想，對當代的職校數學教育有重要的現實價值。教師在教學實施過程中，要自覺利用這些教育思想，來指導自己的教學行為。如，以《大學》中提出的“知止”“知所先后”“明明德”等理念，結合橢圓標準方程的教學，探究傳統文化在具體教學實施過程中的滲透。

（一）知止

《大學》中明確指出學習要“知止”，也就是要確定教學目標。教師在進行數學教學時，也應當首先根據不同類型的學生和學習內容來確定教學目標，要將數學理論的學習和學生的專業特色結合起來。以機電專業為例，多門專業課程的學習需要橢圓標準方程的數學支持（見表1）。教師確立橢圓的教學目標時，需要考慮數學學科內部的需要，也要考慮其他學科的需要，更要考慮學生的文化需要。

（二）知所先后

教學實施的關鍵在于讓學生明白知識的本末及道理。從橢圓的發現到橢圓標準方程的推出，經歷了漫長的歷史過程。數學課堂教學時往往只截取人類認識橢圓的最后三個階段，即從“以繩作橢圓圖形→得出第一定義→推導標準方程”這三個環節來進行教學實施。這樣的處理方法簡潔高效，但不太符合學生對橢圓的認知基礎。但是完全按照人類歷史上對橢圓探究的順序來開展教學，則又顯得格外繁瑣，不能突出重點。教師可以選取以繩作圖之前的部分橢圓概念的關鍵要點，進行課堂重構（見圖3）。這種橢圓概念的呈現方式，結合現代信息技術，做到了教學時間的合理分配。

（三）明明德

教育的根本任務是立德樹人，明德立人。明德就是要在教育教學中弘揚中華民族的優秀品德。在橢圓標準方程的學習中，學生品德培養貫穿課堂始終。在課堂教學開始，讓學生收集身邊的橢圓圖片，在白板上進行展示，以培養學生分享與共贏的觀念;在教學中，通過小組合作探究，推導出橢圓的標準方程，以培養學生團隊合作意識與集體榮譽感;在課末，通過課堂小結，以培養學生善于反思的學術精神;等等。

三、注重隱性資源，感悟傳統文化核心價值觀

在數學教學時，教師除了要關注能直接作用于教學的顯性傳統文化資源，還要善于挖掘隱藏于課程背后的傳統文化核心價值觀。

（一）經世濟用

中國古代學者在進行數學學術研究的時候，注重于理論聯系實際，側重于數學知識的社會效益。在漢代初期，流通的私錢日益增多，貨幣市場異常紊亂，比如朝廷大夫鄧通，自鑄私錢謀利，造成鄧錢遍天下，諸侯國之一的吳，境內銅礦豐富，大肆鑄造私錢，富可敵國，進而引發了七國之亂，造成了國家動蕩。為穩定局面，政府禁止私鑄錢，并對官錢的外觀進行了精心選擇，將流通量最大的三百文面值的銅錢設計為橢圓形。《史記·平準書》中有記載“三曰復小，橢之”。就古代金屬加工的技術而言，橢圓錢幣的制造難度遠大于圓形與方形，所以這種錢幣具有較強的防偽功能。因此，橢圓形錢幣的推出，迅速抑制了漢初貨幣市場的紊亂，有效地維護了國家的穩定與統一。

（二）中庸之道

學生在利用橢圓的第一定義推導標準方程時，經過建系→設點→列式→化簡后，能夠得到表達式： 此時教材中突兀地令 ，將表達式化為 ，進而得到標準方程 。學生一般對此換元的過程比較疑惑，此時教師可以引導學生從簡潔性和對稱性方面來感悟這個換元技巧，橢圓無論是標準方程還是圖形都極具對稱美，對稱美就是數學美的核心。中國古代將這種幾何圖形的對稱美應用到極致，尤其是古代建筑，基本都具有對稱性。這種對稱性，符合中國傳統文化的中庸之道，是中國傳統思想的最高價值原則。中國傳統文化認為，世界上的事物都應具備這種中庸之道，具體體現在做事要不偏不倚、行為要張弛有度，行“中”道才能暗合客觀規律，以便實現“天人合一”的最高理想。

（三）求同尚中

中國古代學者從先秦開始就已經敏銳地意識到事物的兩面性，提出了“一兩”“對待”等辯證原則。中國古代數學的構造性和機械化算法體系固然具有自身的優點，但與西方的數學公理化體系相比，也有很多不足之處。教師在進行橢圓教學時，必須要讓學生正視這種不足。在現代數學體系中，對橢圓研究起促進作用的學者基本都來自西方。比如，洛必達（法國）、但德林（比利時）、舒騰（荷蘭）等，只有認識到差距，才能讓學生樹立迎難而上、追趕超越的決心。當然，中國古代哲學也認為事物發展具有“動靜”“常變”等特質，正如國際知名數學家吳文俊指出：“中國古代數學的構造性和機械化算法體系與西方數學的公理化演繹體系此消彼長，多次反復、遙相呼應。”中國數學的算法系統，在歷史長河中沉寂許久后，正煥發新的能量，對當代數學影響越來越大，這需要教師與學生在進行數學學習時辯證地對待。總之，在數學教學中滲透傳統文化是一項不小的挑戰。它需要數學教師有廣闊的文化視野、豐富的文化儲備，需要全體教師的共同努力。

責任編輯：謝傳兵

收稿日期：2019-03-26

作者簡介：陸宇航，江蘇省通州中等專業學校（江蘇南通，226300）講師，主要研究方向為職業教育數學教學。