在教學中注重培養學生數學抽象核心素養

☉陜西省寧強縣天津高級中學 劉金平

數學抽象是高中數學的六大核心素養之一，是指舍去事物的一切物理屬性，得到數學研究對象的思維過程.抽象函數問題對于高中生來講，難度比較大，不易理解，主要特點是抽象函數的解析式不確定.試題常將函數、方程、不等式和數列等知識結合在一起，考查學生對函數的主要性質（如單調性、周期性、奇偶性和對稱性）的理解能力、邏輯推理能力和抽象思維能力，養成從特殊到一般，從具體到抽象的解題思維習慣.

一、運用函數性質解決問題，培養學生數學抽象概括能力

例1設（fx）是定義在R上的偶函數，其圖像關于直線x=1對稱，對任意的x1，x2∈]，都有（fx1+x2）=（fx1）·（fx2），且（f1）=a＞0.

（2）證明：（fx）是周期函數；

分析：（1）這是根據題干條件求特殊值的問題，需要把1拆成，這樣就可以直接利用條件進行求解；

（2）要利用圖像的對稱性找到對應關系并結合條件就能證明；

解析：（1）因為對于任意的x，x∈]，都有（fx+121x2）=（fx1）·（fx2）成立，

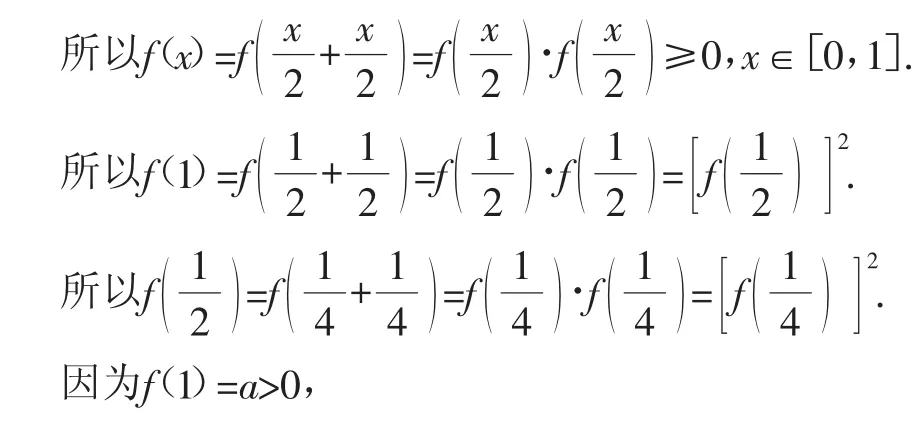
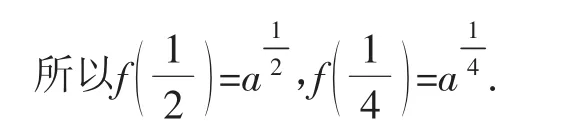
（2）證明：由題意可知，y=f（x）的圖像關于直線x=1對稱，故可得f（x）=f（2-x），x∈R.又由f（x）是偶函數知f（-x）=f（x），x∈R，所以f（-x）=f（2-x），x∈R.將上式中的-x用x替換，得到f（x）=f（x+2），x∈R，

則由周期函數的定義可知f（x）是R上的周期函數，且2是它的一個正周期.

（3）由（1）知f（x）≥0，x∈［0，1］，

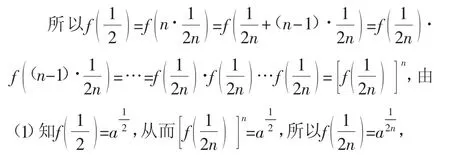
由（2）知（fx）是以2為周期的周期函數，因此，an=

評注：該題主要考查學生對函數的概念、圖像，以及奇偶性、周期性和對稱性等重要性質的理解能力，以及遞推數列等基礎知識的運用能力；考查運算能力、數學抽象能力和邏輯推理能力.關鍵是要緊緊抓住題干條件f（x1+x2）=f（x1）·f（x2）進行適當變形尋找解決問題的突破口，巧妙地將抽象問題具體化.在解題過程中要讓學生體會和感受到解決抽象函數問題的技巧和方法，從而達到落實數學核心素養的目的.

二、借助數學思想方法解決問題，培養學生數學抽象核心素養

例2已知函數f（x）對于任意的x，y∈R都有f（x+y）=f（x）+f（y），且當x＞0時，有f（x）＜0.

（1）求f（0）的值；

（2）判斷f（x）的奇偶性與單調性，并證明你的結論；

分析：（1）由（fx+y）=（fx）+（fy）這個條件求特殊值，只需充分利用自變量取值的任意性就可以完成；

（2）結合題目條件，利用函數的奇偶性和單調性的定義巧妙地對（fx+y）=（fx）+（fy）進行變形即可；

解析：（1）由對于任意的x，y∈R都有f（x+y）=f（x）+f（y）成立，不妨令x=y=0，得

f（0+0）=f（0）+f（0），所以f（0）=0.

（2）根據函數奇偶性的定義，由（1）知，可令y=-x，得f（x-x）=f（x）+f（-x），

即f（0）=f（x）+f（-x），而f（0）=0，所以f（-x）=-f（x）.故f（x）為奇函數.

由函數單調性的定義，任取x1，x2∈（-∞，+∞），不妨設x1＞x2，則x1-x2＞0，由題設條件得f（x1-x2）＜0.

而f（x1-x2）=f（x1）+f（-x2），所以f（x1）+f（-x2）＜0，

即f（x1）＜-f（-x2）=f（x2）.所以f（x）在（-∞，+∞）上為減函數.

（3）因為函數（fx）是奇函數且當x＞0時，（fx）＜0，當x∈［-1，1），x-1＜0，得（fx-1）＞0，所以＜2k可變形為（fx2+1）＜2k（fx-1）.

①當k∈Z+時，由數學歸納法可證得2k（fx）=（f2kx）.（*）

②當k=0時，（*）式顯然成立；當k＜0時，由奇函數的性質可證明（*）式也成立.

所以有（fx2+1）＜（f2kx-2k），由單調性得x2-2kx+1+2k＞0，對于x∈［-1，1）恒成立.運用分離參數法可變形為在x∈［-1，1）上恒成立，

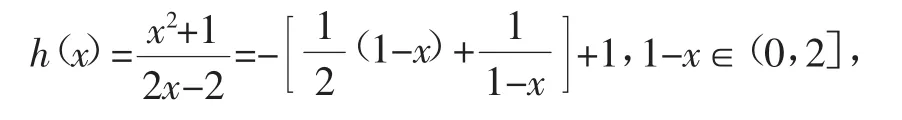
評注：前兩個問題采用“賦值法”就可以輕松解決，由定義域的一般性給變量賦特殊值即可，第三個問題則利用函數的單調性將抽象函數轉化為求具體函數的最值問題，運用轉化與化歸的數學思想使問題得以解決，這是解決抽象函數問題的常用方法，在教學過程中要善于引導學生去感受、體會這種解題思路，不斷積累經驗，養成自覺運用數學抽象思維解決問題的良好習慣.

在高中數學課程的學習過程中，由于學生對高中數學知識的認知能力有限，還未形成系統的數學知識體系，從一個數學情境中抽象概括出一個數學模型的能力比較欠缺，這兩個例子所給出的函數關系分別可以抽象為指數型函數f（x）=ax和一次函數f（x）=kx模型，這是學生最熟悉最易理解的兩個函數模型，把抽象的不好理解的數學問題轉化成學生熟悉的常見的數學問題，符合學生的認知規律，從而激發了學生學習數學的信心和興趣，對培養學生學習數學的思維品質和提升學生的數學核心素養都有較大幫助.W