例談“等時圓周”結論在動力學中的應用

徐美獎　王燕萍

摘要：對于比較幾個質點在圓周或類似圓周情景中的運動時間的動力學問題，重點考查運動學和牛頓第二定律的基本規律.筆者通過對該類問題的研究，歸納出“等時圓周”結論，本文從兩個方面分析“等時圓周”結論在動力學中的應用.

關鍵詞：等時圓周;動力學;模型應用

1 基本模型及規律

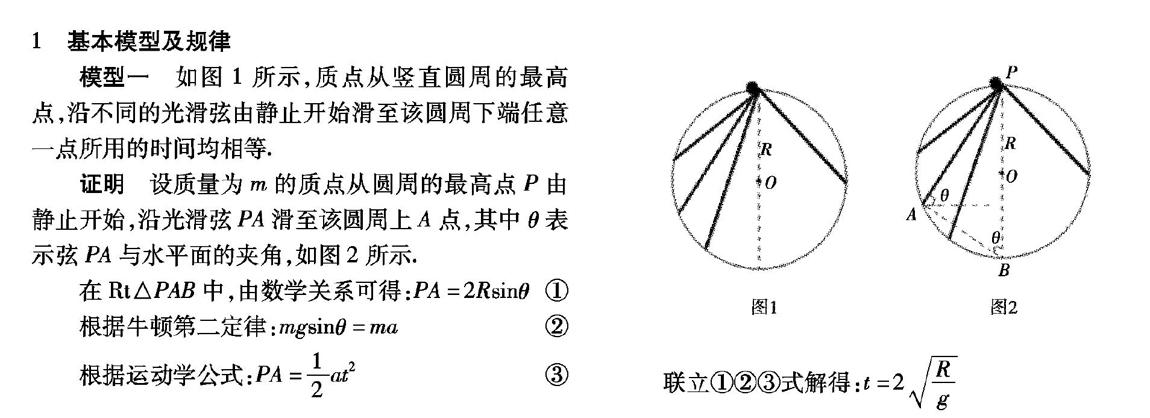
模型一如圖1所示，質點從豎直圓周的最高點，沿不同的光滑弦由靜止開始滑至該圓周下端任意一點所用的時間均相等.

證明設質量為m的質點從圓周的最高點P由靜止開始，沿光滑弦PA滑至該圓周上A點，其中θ表示弦PA與水平面的夾角，如圖2所示，

在Rt△PAB中，由數學關系可得：PA= 2Rsinθ①

根據牛頓第二定律：mgsinθ= ma

②

根據運動學公式：PA=1/2at²

③

可見運動時間t為定值，與到達圓周下端點的位置無關.

模型二如圖3所示，質點從豎直圓周上端任意一點，沿不同的光滑弦由靜止開始滑至該圓周的最低點所用的時間相等.

證明 設質量為m的質點從圓周上端任意一點A由靜止開始，沿光滑弦AP滑至該圓周的最低點P，其中θ表示弦PA與水平面的夾角，如圖4所示，

在Rt△PAB中，由數學關系可得：AP= 2Rsinθ①

2 典例賞析

例1如圖5所示，位于豎直平面內的固定光滑圓環軌道與水平面相切于M點，與豎直墻相切于A點.豎直墻上另一點B與M的連線和水平面的夾角為600，C是圓環軌道的圓心.已知在同一時刻，a、b兩球分別由A、B兩點從靜止開始沿光滑傾斜直軌道AM、BM運動到M點，而c球由C點自由下落到M點，則（ ）

A.a球最先到達M點

B.b球最先到達M點

C.c球最先到達M點

D.b球和c球都可能最先到達M點

點評 首先分析清楚各研究對象的運動情況是關鍵.其次，本題可巧妙地結合“等時圓周”的結論，進行定性分析，a球的運動時間等于一個“等時圓周”的時間，b球的運動時間大于一個“等時圓周”的時間，c球的運動時間小于一個“等時圓周”的時間，故c球最先到達M點.

例2 如圖7所示，光滑細桿BC、DC和AC構成矩形ABCD的兩鄰邊和對角線，AC：BC： DC =5：4：3，AC桿豎直.各桿上分別套有一小球a、b、d（可視為質點），a、b、d三小球的質量比為1：2：3.現讓三小球同時從各桿的頂點由靜止釋放，不計空氣阻力，則o、b、d三小球在各桿上滑行的時間之比為（ ）

A.1：1：l

B.5：4：3

C.5：8：9

D.1：2：3

解析 根據題設中所給的數學關系可知，該矩形的四個頂點位于以AC邊長為直徑的圓周上，如圖8所示，故三個小球a、b、d的運動滿足“模型二”中的情景，由“等時圓周”結論可知，它們的運動時間相等，所以選項A正確.

點評 利用數學知識解決物理問題是一項重要能力，本題要求學生能發現其中數學關系，并聯系物理“等時圓周”模型，同時考查思維遷移能力，如果學生沒有聯想到用此模型的結論來求解，而是通過位移關系并運用動力學知識去計算小球的運動時間，將會花費較多時間.

例3 如圖9所示，在傾角為θ的斜面上A點有一長為L= lOm的輕桿豎直放置.已知A點距斜面底端lOm，現從輕桿頂端B點處安裝一滑索到斜面底端，不計摩擦阻力，取g=lOm/s²，則一可套在滑索上的小球從B點由靜止開始滑到斜面底端的時間為（ ）

A.Is

B.√2s

C.2s

D.4s

點評 學生在求解本題時，分析小球沿滑索下滑做勻加速直線運動，可能會糾結如何表示其加速度和位移，而無法繼續進行下去.如果我們巧妙地利用題于中的長度關系構建一個圓，就大大簡化了過程分析，再直接利用“等時圓周”結論進行計算就顯得非常簡便.

點評 學生在解答本題容易錯誤套用“等時圓周”結論，而錯選A選項.其實本題中三個小環下滑至a點并非圓周的最低點，因此本題應用動力學知識來求解.

變式應用2 如圖12所示，在傾角為θ的斜面上方的A點處旋轉一光滑的木板AB，B端剛好在斜面上.木板與豎直方向AC所成角度為a，一小物塊自A端沿木板由靜止滑下，要使物塊滑到斜面的時間最短，則a角與θ角的大小關系應為（ ）

A.a=θ

B.a=θ/2

C.a=θ/3

D.a =20

解析 利用數學知識分析可知，要使物塊從A點滑到斜面的時間最短，我們可以作一個合適的圓，這個圓的圓心在AC上，同時也經過A點.當這個圓恰好與斜面相切時，切點記為B，從A點到B點連線的方向就是木板AB應該放置的方向，如圖13所示，再利用“等時圓周”結論可知，這樣所用的時間最短.由數學關系知，∠COB=θ，∠OAB=∠OBA=a，根據三角形知識得θ=2a，即a=θ/2，故選項B正確.

點評 本題所求時間最短問題，學生不易想到對應何種情景，但是如果學生對“等時圓周”模型及規律非常熟悉，運用數學知識做出圓并與斜面相切其實就是我們要找的情景，這個問題就變得容易理解了.

參考文獻：

[1]教育部課程教材研究中心所.普通高中課程標準實驗教科書物理必修2教師用書[M].北京：人民教育出版社，2013.

[2]江四喜.高中物理經典名題精解精析[M].合肥：中國科學技術大學出版社，2018.

[3]鐘小平.高中物理競賽題典習題全解[M].杭州：浙江大學出版社，2012.

（收稿日期：2019 - 01 -15）