直觀想象素養在求解函數壓軸小題中的滲透

趙志剛

摘要：新修訂的《普通高中數學課程標準（2017年版）》中強調：突出數學素養，在數學課程逐漸展開的過程中，促進學生數學核心素養的形成和發展，本文例談直觀想象數學核心素養在導數背景下的函數、不等式問題中的滲透，

關鍵詞：直觀想象;導數;函數;不等式

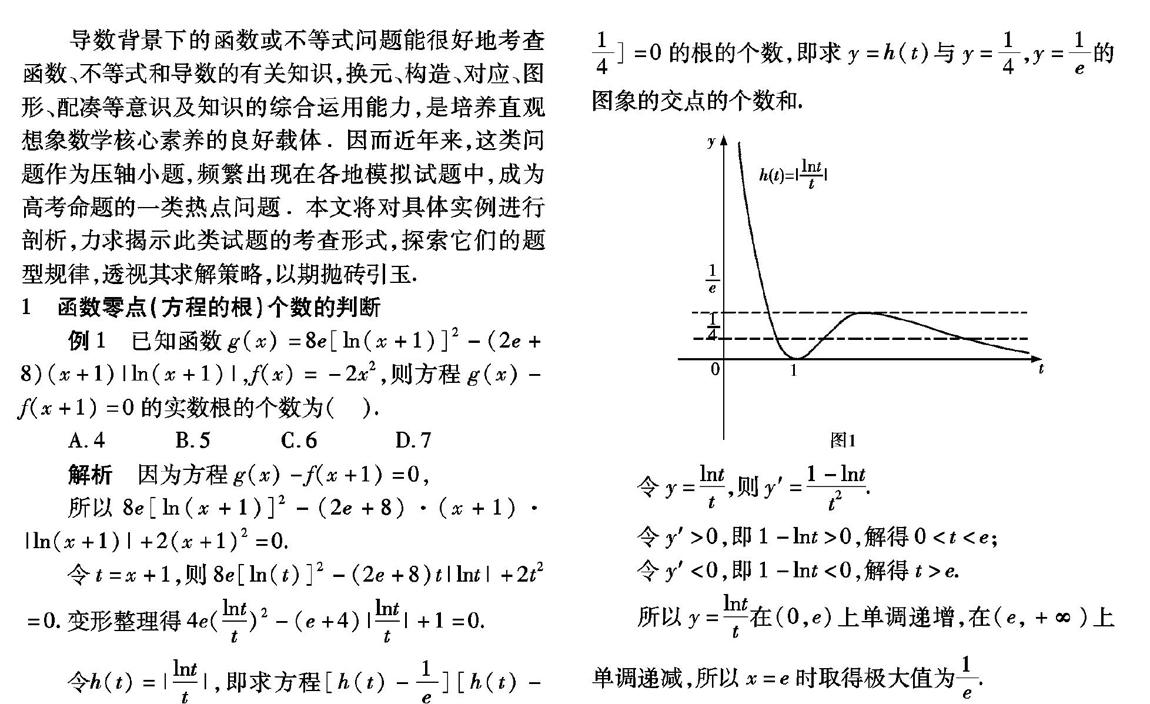
導數背景下的函數或不等式問題能很好地考查函數、不等式和導數的有關知識，換元、構造、對應、圖形、配湊等意識及知識的綜合運用能力，是培養直觀想象數學核心素養的良好載體.因而近年來，這類問題作為壓軸小題，頻繁出現在各地模擬試題中，成為高考命題的一類熱點問題.本文將對具體實例進行剖析，力求揭示此類試題的考查形式，探索它們的題型規律，透視其求解策略，以期拋磚引玉.

評注 本題以方程根的個數判斷為背景，考查了方程與函數轉化、換元、導數在研究函數的單調性中的應用等知識，最后結合圖象作出判斷，很好地考查了直觀想象、數學運算和邏輯推理等數學核心素養.

2 函數方程中關系式的求解值問題

評注 本題依據目標式的結構特征，換元轉化為新元的一元二次方程后利用韋達定理，并結合導函數與原函數的單調性的關系，作出圖象整體求解.很好地考查了換元轉化、整體處理的意識和直觀想象、邏輯推理等核心素養的運用.

3 函數方程中參數范圍的確定

評注 解決此類問題往往將問題轉化為方程根的問題，再轉化為兩函數圖象的交點問題來解決.本題主要考查函數與導數的綜合應用以及直觀想象的數學核心素養.

4 函數不等式中參數范圍的確定

例4（2019屆“超級全能生”聯考理16）設m∈

評注 本題充分挖掘函數式所蘊含的幾何背景，將不等式成立轉化為最值問題，進而構造函數，利用導數的幾何意義求解，充分體現直觀想象數學核心素養的運用.

評注 本題基于高考的函數與導數的綜合應用，考查轉化能力，計算能力以及數形結合思想命制，在分類討論的基礎上結合圖象進行求解，很好地考查了直觀想象、邏輯推理和數學運算等數學核心素養.5感悟

英國數學家懷特·海德說過：“數學是從模式化的個體作抽象的過程中對模式的研究.”羅增儒教授也說過：“學習數學的過程中，所積累的知識經驗經過加工，會得出有長久保存價值或基本重要性的典型結構與重要題型——模式，將其有意識地記憶下來.當遇到一個新問題時，我們辨認它屬于哪一類基本模式，聯想起一個已解決問題以此索引，在記憶存儲中抽取相應的方法來解決，這就是模式識別的解題策略.”如果學生對平時的問題善于總結、積累，那么在以后的解題中，就可以迅速地把新問題轉化為已掌握的類型.直觀想象作為作為六大數學核心素養之一，恰當而合理的使用，確實會給一些數學問題的解決帶來事半功倍的效果，就像以上例題中看到的，導數本身就是研究函數性質的有力工具，有同學曾感慨道，導數的學習給函數的研究插上了翅膀，而其背景下直觀想象素養有效運用，相當于給函數的研究又插上了一只翅膀，展開雙翅，這樣也許就會飛的更高、更遠.

新一輪的課程改革已經進入了關鍵時期，在教育教學中越來越強調要培養學生的數學核心素養和學習能力.近年來，高考制度的改革給高中數學教學也帶來了深刻的變革，在復習中教師越來越注重學習方法、解題方法的傳授，而不僅僅只是向學生傳授基礎的學科知識.數學是學生學習生涯中促進其能力發展、思維提高以及認知水平提高的一個基礎性學科.但是由于高中數學知識的復雜性、抽象性使很多學生在學習過程中望而生畏.教師在數學解題教學中教學方式以及教學理念若運用不當，就會使得學生的學習效率低下，表面上每天都沉浸在高壓的學習下，但是并沒有什么太大的效果.因此，教師必須要轉變教學理念和教學方式，引導學生對不同類型題目的特征進行總結和歸納，掌握不同的解題方法，讓學生在做題實踐中體會數學的魅力，

參考文獻：

[1]中華人民共和國教育部.普通高中數學課程標準（2017年版）[M].北京：人民教育出版社，2018.

[2]蔡勇全.承載函數壓軸小題的兩個新熱點——x/e^x與lnx/x.理科考試研究，2019（1）1 -4.