例談“數形結合思想”在高考中的靈活應用

魏建平

摘要：數形結合思想是高中數學中的一個很重要的數學思想，也是解題的一種重要依據.本文以2018年高考數學全國I卷（理）為例，說明數彤結合思想在解高考數學有關問題時的應用.由形化數、由數化形、數形轉化是本文永恒的主題，也是解決問題的關鍵之所在.

關鍵詞：數形結合;由形化數;由數化形;數形轉化

數形結合思想是解答數學試題的一種常用方法與技巧，特別是在解決選擇、填空題時發揮著奇特功效，數形結合，由數思形，由形定數，起到互補、互動、互譯作用，可見數形結合思想可以使某些抽象的數學問題直觀化、生動化，能夠變抽象思維為形象思維，有助于把握數學問題的本質.運用數形結合思想解題通常有三種類型：由形化數，由數化形，數形轉化，下面舉例說明.

1 由形化數

由形化數就是借助所給的圖形，仔細觀察研究，提出圖形中蘊含的數量關系，反映幾何圖形內在的屬性.

例1 （2018年全國I卷理10）如圖1來自古希臘數學家希波克拉底所研究的幾何圖形.此圖由三個半圓構成，三個半圓的直徑分別為Rt△ABC的斜邊BC，直角邊AB，AC.△ABC的三邊所圍成的區域記為I，黑色部分記為Ⅱ，其余部分記為Ⅲ，在整個圖形中隨機取一點，此點取自I，Ⅱ，Ⅲ的概率分別記為p1，p2，p3，則（ ）.

點評 本題主要考查幾何概型與數形結合的數學思想.解答本題的關鍵是借助所給的圖形，仔細觀察研究，提出圖形中蘊含的數量關系，計算出半圓、三角形等幾何圖形的面積，然后再找p1，p2，p3之間的關系.

2 由數化形

由數化形就是根據題設條件正確畫出相應的圖形，使圖形能充分反映出它們相應的數量關系，提煉出數與式的本質特征，

例2（2018年全國I卷理6）在△ABC中，AD為BC邊上的中線，點E為AD的中點，則贏：（ ）.

點評 本題以向量與三角形為背景，考查向量的線性運算、向量加法的平行四邊形法則、數形結合思想等知識.解答本題的關鍵是根據題設條件正確畫出相應的圖形，使圖形能充分反映出它們相應的數量關系，提煉出數與式的本質特征，然后利用向量的線性運算、向量加法的平行四邊形法則等知識求解.

3 數形轉化

數形轉換就是根據“數”與“形”既對立，又統一的特征，觀察圖形的形狀，分析數與式的結構，引起聯想，適時將它們相互轉化，化抽象為直觀并提示隱含的數量關系.

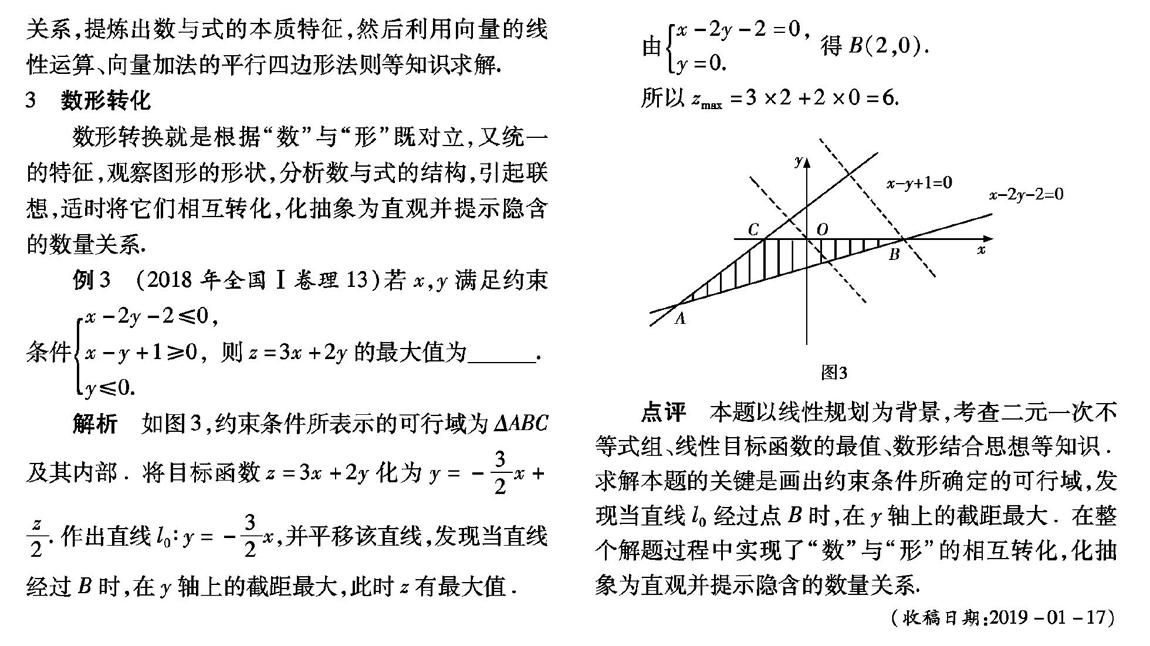
點評 本題以線性規劃為背景，考查二元一次不等式組、線性目標函數的最值、數形結合思想等知識.求解本題的關鍵是畫出約束條件所確定的可行域，發現當直線Z。經過點B時，在y軸上的截距最大.在整個解題過程中實現了“數”與“形”的相互轉化，化抽象為直觀并提示隱含的數量關系.

（收稿日期：2019 - 01 - 17）