明“理”解困以“理”入法
——“小數除法”教學難點的破解策略

吳央軍 呂春女

一、緣起：事物反常必有因

在一次小學數學期末質量監測中，有兩道考查“小數除法計算”的試題出現了“反常”的低得分率。所謂反常：一是該題預計難度系數與實測難度系數相差甚遠；二是該題與其他計算題的得分率相差甚遠。我們來看：

題一是一道小數除法的計算題，考查的知識有兩點：一是小數除法的計算；二是求商的近似值。全縣參考人數為6407人，預計得分率為75%，實際得分率只有56%。題二雖然是以填空題形式出現，考查的卻是學生對計算過程中對小數除法豎式中各部分意義的理解。因此從廣義上講，這也是一道小數除法的計算題。本題預計得分率為70%，實際學生的得分率是50.1%。除此兩題外，其余計算題的得分率均超過80%。

這引起了筆者的思考，對學生來說“小數除法計算”為什么會比其他計算要難？難在什么地方？

二、由現象觀本質：小數除法計算難點分析

根據樣本數據分析，主要有以下幾個方面。

1.小數除法轉化難度較大。

計算一個數除以小數，要將除數轉化成整數，為了保持商不變，被除數也應該擴大相應的倍數。列豎式計算式時，要通過小數點的移動來實現這一轉化，外顯特征為小數點位置的變化。這一變化實際包含兩個步驟（以1.55÷3.9為例）：一是移動除數的小數點，將除數轉化成整數。即3.9轉化成39，相當于將除數擴大到原來的10倍。二是移動被除數小數點，將被除數也擴大到原來的10倍。顯然，這對于學生來說并不是一件容易的事。

如圖1所示，該題轉化過程出現了錯誤，除數的小數點向右移動了一位，被除數的小數點卻向右移動了兩位。為什么會出現這種情況呢？這是因為，“1.55÷3.9”被除數的小數位數比除數多，這種類型的題目例題中并沒有單獨安排，只是在“做一做”中以練習的形式出現。

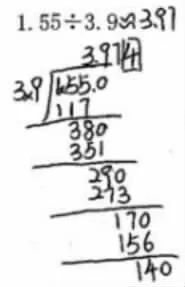
圖1

反觀“一個數除以小數”的例題，如下圖2：

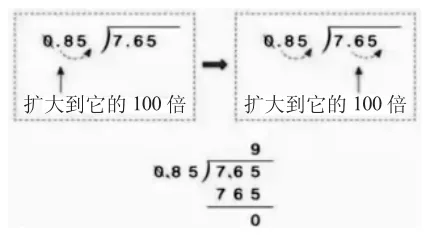
圖2

7.65÷0.85的豎式，被除數與除數的小數位數相同，這是最簡單的情況，只要同時撇去被除數與除數的小數點，就實現了全部的轉化過程。該學生可能受此外顯操作遷移，認為所有的小數除法都是只要把被除數與除數的小數點同時撇去就可以，于是得出“商的小數點與被除數的末位后面對齊”這樣一個錯誤的結論。

2.對算式中各部分意義理解困難。

小數除法的計算中將除數轉化成整數來計算后，學生對除法豎式中每一步所表示的意義的掌握感到困難。以“一根4.88米的木料，每0.12米鋸一段，可以鋸（ ）段，還余（ ）米”為例，豎式如下圖3：

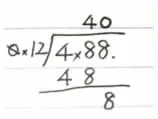
圖3

豎式中，被除數“4.88”表示這根木料全長4.88米，除數“0.12”表示每0.12米鋸一段，商“40”表示可以鋸成這樣的40段，余數“8”實際上是“8 個 0.01”，表示還余下0.08米。學生對此卻沒有清晰的理解。據樣本數據分析，學生錯誤情況主要集中表現為以下幾種：

圖4

圖5

圖6

可以看出學生對算式各部分意義的理解存在困難，具體表現在以下幾個方面：

（1）對商中每個數位上的數表示的意義理解困難。

筆者認為，圖4答案的整數部分出現錯誤，并非小數點位置的錯誤，而是另有原因。我們來還原計算過程，如下圖7：

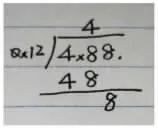
圖7

我們發現，學生計算4.88除以0.12時，將原式轉化成488除以12計算，在十位上商8，個位移下來，不夠商1，計算就此結束，從而得出商4余數0.08的錯誤結論。轉化后，學生對每個數位上商所表示的意義不是很清晰，錯將4個十當成了4個一，造成商末尾的0漏掉了。不僅如此，我們還發現該同學對“余下幾米”這個問題也曾糾結，可見對除數和余數的區分也不是很清晰。

（2）將商的小數部分錯當余數。即圖5答案。那么這種情況是怎么來的呢？我們來看豎式，如下圖8：

圖8

學生對商的小數部分理解錯誤，錯將商的小數部分當作余下的米數。從學生的修改痕跡來看，學生僅在糾結用循環小數還是用近似值來描述，殊不知該“0.7”表示的只是剩下的米數約能做0.7根，而不是還余0.7米。

（3）對余數的意義理解困難。即圖6答案。根據商不變性質，將“4.88÷0.12”轉化成“488÷12”后，商不變，余數卻隨著被除數與除數的變化，擴大到原來的100倍，因而求原來的余數，應將8縮小回原來的100倍，即0.08。學生因對商不變性質理解不到位，將兩者完全等同起來，錯將轉化后的余數“8”理解為“8 個 1”，從而得出還余8米的結論。

3.整數除法遺留問題較多。

除了轉化有難度外，我們發現除法計算過程出現的情況也較為復雜，其中很大一部分為整數除法難點的遺留。還以“1.55÷3.9”為例，主要表現在以下幾個方面：

（1）同一數位多次求商。如下圖9：

圖9

學生將 1.55÷3.9轉化成15.5÷39后，十分位上商3余38，又用“38”除以除數，在百分位上商“0”。在這里“38”表示十分位除后還余38個十分之一，要先添“0”，變成380個百分之一，再除以39。要解決這種錯誤，學生必須明白每一步表示什么意義，正確掌握“除到哪一位商就寫在那一位的上面”。這樣才不會出現同一數位多次求商的現象。

（2）初商過小不會調。如下圖10：

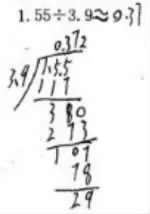
圖10

除法中，遇到某次余數沒有比除數小，說明初商過小，只需要把商調大。上述學生在百分位上商 7 后，余數是“107”大于“39”，卻沒有將百分位上的商調大，而是又用39去除了一次。究其原因，也是對算理的理解不夠透徹，他不明白第二次用39去除107得到的商2還表示2個百分之一，和原來的7個百分之一合起來是9個百分之一，只需要在百分位上寫9，而不是把2寫在千分位上。

（3）進位退位容易錯。如下圖11、12：

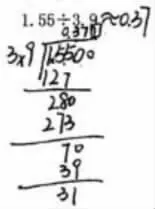
圖11

圖12

一個除法豎式，簡直是加、減、乘、除大集合，若遇除數數值偏大，計算難度就增加。上述兩種錯誤并非個別現象，據抽樣分析，錯誤學生中，約有30%是因為進位、退位不熟練造成的。

三、據成因找對策：小數除法難點破解

1.厘清轉化類型，抓住本質要素。

對學生來說，小數除法轉化為整數除法的過程較為復雜，具體細化為下面幾種情況：

（1）除數是一個整數的。如22.4÷4，可以直接除，需要注意的是商的小數點與被除數的小數點對齊。

（2）被除數是一個整數。如23÷1.5，列豎式時需要把被除數和除數同時擴大到原來的10倍，即小數點向右移動一位。外顯操作為在撇去除數小數點同時需要在被除數末尾添0。

（3）除數的小數位數比被除數少。如1.55÷3.9，列豎式時需要把被除數和除數同時擴大到原來的10倍，即小數點向右移動一位。外顯操作為在撇去除數小數點，撇去被除數“1”后小數點同時再往右數第一位數“5”的后面點上新的小數點。

（4）除數的小數位數比被除數多。如12.6÷0.28，列豎式時要把小數點向右移動兩位，被除數小數位數不夠時需要用“0”補足。外顯操作為撇去除數小數點和“0”，再撇去被除數小數點后同時添上一個“0”。

（5）除數的小數位數與被除數相同時。如11.7÷2.6，豎式計算時只需將被除數和除數同時擴大到原來的10倍。外顯操作為同時撇去除數和被除數的小數點。

當情況變得復雜的時候，學生就容易出現錯誤。糾正這樣的錯誤，需要幫助學生抓住本質要素。所有的轉化類型，其依據都是“商不變性質”。夯實“商不變性質”，可幫助學生清晰掌握算理——將被除數和除數的小數點同時向右移動相同的位數，商保持不變。同時清晰掌握算法——把被除數和除數的小數點同時向右移動相同的位數，將除數轉化成整數計算。只有這樣，學生面對具體情況時才能思路清晰，轉化正確。

2.借助“故事”背景，落實“循理入法”。

教材在編排小數除法的學習時，并不單以算式的形式出現，而是結合具體的情境出現。因此，教學中我們要充分利用問題的“故事”情境，結合學生的生活經驗和已有知識，引導學生自主探索小數除法的計算方法，理解小數除法的算理。

（1）借“故事”明算理。以題二為例，“一根4.88米的木料，每0.12米鋸一段，可以鋸（）段，還余（）米”。可以借助米與厘米之間的關系來溝通“商不變性質”，將問題轉化成求“488厘米里有幾個12厘米”，這就相當于將“被除數和除數同時擴大100倍，商不變”。引導學生發現其共同點都是將除數是小數的除法轉化成除數是整數的除法，從而進一步理解小數除法的算理。同時結合具體情境，理解除法豎式中每一步所表示的實際意義，這樣余數“8”表示還剩8厘米，即0.08米。

（2）為算理找“故事”。例如計算“1.55÷3.9”時，引導學生思考：可以借助什么“故事”來溝通算理，除了利用長度單位還有什么辦法嗎？讓學生自主編出合理的“故事”以解釋算理。學生通過思考、討論，明白要將除數轉化成整數來計算，需要把除數和被除數同時擴大到原來的10倍，進率為十的量都可以用來溝通。為算理找“故事”讓商不變性質不再抽象，讓小數除法的算理找到落腳點。

3.精心設計練習，跟進“以理馭法”。

很多教師在新授課中都比較重視在理解算理的基礎上總結算法，學習計算后通常設計“計算”與“解決問題”來跟進算法的鞏固，而忽視算理的練習。事實上，除此之外還需要在練習中加以鞏固學生對算理的理解。讓學生不只是盲目地記住怎樣操作，而是充分理解算理之后的算法概括，從而真正提升計算素養。

（1）“有理說得清”——讓“說理”成為常規性作業。利用好教材的例題及練習題，在小數除法新課學習后可以要求學生自由選擇某一豎式同桌互說算理、算法，說清楚如何轉化，依據什么性質。例如下題（圖13）：

圖13

可以計算之前說說怎樣移動小數點，為什么這樣移動；也可以計算之后說說怎么算的，每一步表示什么；或者可以結合具體情境，用情境解釋算理。

（2）“有理寫得明”——讓“明理”成為可外顯練習。與說相比，用文字把思考過程寫出來，經過更多的整理外化，在寫的過程中增加了調整的機會，讓計算思維變得外顯而可操作。如下圖14：

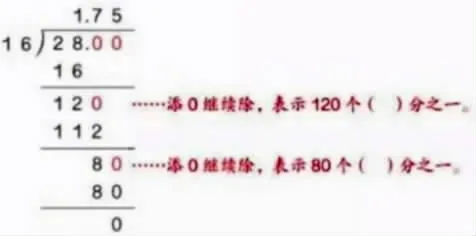
圖14

教材中的例題給我們提供了很好的典范，只要稍加利用，進行追問或改編，就可以成為針對性的算理練習。從而使學生在練習中強化算理與算法的結合。

（3）“有理評得出”——讓“算理”成為可測試問題。我們應該在平時評價中自主設計需要利用算理進行解釋的問題，并在階段性測試中增加此類要求，以增加學生的重視程度，檢測學生理解的程度。

4.夯實除法基礎，逐漸螺旋上升。

筆算除法的得分率比其他運算要低，這是由除法豎式本身的特點決定的。整數除法中常見的錯誤在小數除法中也會經常出現。要解決這些錯誤，就要夯實筆算除法的基礎。二年級第一次接觸到筆算除法時，可以結合實物、圖像，幫助學生理解除法豎式的意義、寫法；三年級學習除數是一位數的除法時，鞏固二年級豎式的寫法。在此基礎上結合算理，讓學生明確算法，掌握“除到哪一位商就寫在那一位上面”，明白同一數位不可以多次求商；四年級學習除數是兩位數的除法時，鞏固二、三年級的知識，在此基礎上學習除數是兩位數的除法試商、調商、求商；五年級學習的小數除法，是在二、三、四年級的基礎上，進一步將除數是小數的除法轉化成除數是整數的除法計算。在螺旋上升的過程中，每一個易錯點將反復出現，必須加強鋪墊與練習，以彌補薄弱，突破難點，讓學生在反復更正中不斷進步。