基于多尺度排列熵的艦船輻射噪聲復雜度特征提取研究

陳 哲， 李亞安

(西北工業(yè)大學 航海學院，西安 710072)

艦船輻射噪聲是被動聲吶進行目標檢測、跟蹤、識別、定位的信號源，研究艦船輻射噪聲的特征提取有助于提高被動聲吶的工作性能，具有重要的實際工程意義[1-3]。

由于產(chǎn)生機理復雜，且受到復雜水下海洋環(huán)境的影響，艦船輻射噪聲通常具有非平穩(wěn)、非高斯、非線性的“三非”特性，使得從中提取穩(wěn)定特征成為水聲領域研究的難點。傳統(tǒng)艦船輻射噪聲特征提取方法如短時傅里葉變換、功率譜分析[4]、LOFAR譜分析[5]、小波變換[6]等已被實踐證明不適用于水聲信號處理[7-8]。近年來，經(jīng)驗模態(tài)分解(Empirical Mode Decomposition, EMD)[9]與集成經(jīng)驗模態(tài)分解(Ensemble Empirical Mode Decomposition, EEMD)[10]的提出為艦船輻射噪聲特征提取問題的解決提供了新的思路[7-8,11-13]。劉深等[13]利用EMD分析了艦船輻射噪聲各階固有模態(tài)函數(shù)(Intrinsic Mode Function, IMF)的能量譜；楊宏等[7]分析了艦船輻射噪聲高頻IMF與低頻IMF之間的能量差；李余興等[8]利用EEMD分析了艦船輻射噪聲最強IMF的中心頻率。這些方法取得了一定的分類效果，但樣本種類較少，且都只從單一尺度上分析了艦船輻射噪聲。

通常來說，信號的非線性越強，其規(guī)則性越弱，可預測性越小，復雜程度越高。鑒于艦船輻射噪聲具有強非線性，有必要從復雜度的角度對其加以研究。隨著非線性動力學的發(fā)展，使得表征信號的復雜程度成為可能。至今，已有多種表征時間序列復雜度特征的方法如：關聯(lián)維數(shù)[14]、樣本熵[15]、多尺度排列熵[16-17]等。其中，多尺度排列熵所需運算量小、穩(wěn)定性強、具有多維分析能力，已被廣泛應用于故障診斷領域[18-20]。這些應用的成功表明了多尺度排列熵對復雜信號強大的處理能力。

結合水聲信號的“三非”特點，針對以上艦船輻射噪聲特征提取存在的問題，本文提出一種基于多尺度排列熵的艦船輻射噪聲特征提取方法，從復雜度的角度研究水聲信號。首先，將實測艦船輻射噪聲按尺度分解為一系列子序列，并計算各尺度子序列的排列熵，得到艦船的多維多尺度排列熵特征。進一步，將所提取的艦船多尺度排列熵特征輸入概率神經(jīng)網(wǎng)絡(Probability Neural Network, PNN)[21]進行分類驗證，實驗結果表明了該方法的有效性。

1 多尺度排列熵

排列熵是一種能有效度量信號復雜程度的物理量，信號越復雜，排列熵值越高，反之，則熵值越低。例如，白噪聲的排列熵值最大而正弦信號的排列熵值最小。

多尺度排列熵是排列熵的改進，其思想是先將時間序列進行多尺度分解，再計算各尺度子序列的排列熵，進而從多個維度描述信號的復雜度。給定一維時間序列{x(i),i=1,2,…，N}，將其按式(1)進行多尺度分解：

(1)

式中:s為尺度因子，1≤j≤N/s，ys為尺度s下的子序列。對尺度s下的子序列，按如下步驟計算其排列熵：

1)適當選取嵌入維數(shù)m與時間延遲τ，按式(2)重構其相空間：

(2)

式中：Ys為重構矩陣，K=N/s-(m-1)τ。

ys(t+(j1-1)τ)≤ys(t+(j2-1)τ)…≤ys(t+(jm-1)τ)

(3)

令πt={j1,j2…jm}表示該行各元素的原始位置，則πt表征了該行的排列方式。顯然，Ys中的任一行均有m！種可能的排列類型，對每一行重復上述步驟，統(tǒng)計得到每種排列類型出現(xiàn)的頻數(shù)hl與概率pl=hl/K。

3)根據(jù)式(4)計算得到尺度s下子序列的排列熵：

(4)

進一步，對其他尺度下的子序列按上述步驟計算其排列熵，便可得到原始時間序列的多尺度排列熵。在計算多尺度排列熵時，原始時間序列的長度N，尺度因子s，嵌入維數(shù)m和時間延遲τ的選取至關重要。根據(jù)前人的研究結果[22-23]與大量實驗研究，本文取N=8 820，s=1～10，m=3，τ=1。

2 特征提取

本文對五類實測艦船輻射噪聲進行特征提取實驗。艦船輻射噪聲數(shù)據(jù)采集自中國南海，實驗位置水深約4 000 m，海底近似平底，數(shù)據(jù)采集在一級海況條件下進行，風浪噪聲較小。全向水聽器由實驗船布放至水下30 m處，水聽器靈敏度為-170 dB re 1v/μpa，頻率響應為0.1 Hz～80 kHz，水聽器另一端與采樣頻率為44.1 kHz的數(shù)字采集儀相連。為減小自噪聲對信號采集的影響，實驗船發(fā)動機在數(shù)據(jù)采集過程中熄火。水聽器布放完成后，五類艦船先后以8節(jié)航速在實驗船1 km外航行。本文特征提取實驗中，每類艦船各有148個樣本，每個樣本包含8 820個數(shù)據(jù)點(0.2 s)。為了分析、比較多種特征提取算法的優(yōu)劣，本文分別利用基于EEMD的最強IMF中心頻率法、高低頻能量差法與基于復雜度的排列熵和多尺度排列熵分析以上數(shù)據(jù)。

2.1 基于EEMD的特征提取

利用EEMD對五類艦船輻射噪聲進行模態(tài)分解，結果如圖1所示。可以看出，EEMD將各類艦船輻射噪聲分解為一系列從高頻到低頻排列的IMF。由于EEMD是一種自適應的模態(tài)分解方法，因此，不同類別艦船輻射噪聲分解后得到的IMF階數(shù)不同，圖1僅列出有代表性的前六階IMF。對這些能反映信號不同振動狀態(tài)的IMF進行信息挖掘，便可得到不同類別艦船輻射噪聲的振動特征。

圖1 五類艦船輻射噪聲的EEMD分解

采取與文獻[8]相同的IMF中心頻率、平均強度定義，對五類艦船輻射噪聲進行分析，圖2和表1分別給出了五類艦船各148個樣本最強IMF中心頻率的分布情況和統(tǒng)計特性。可以看出，除第二類艦船有少量離群值外，第一、二、三、五類艦船的最強IMF中心頻率分布范圍相對固定，最強IMF中心頻率的均值相差較大，可分性強。但是，第四類艦船的最強IMF中心頻率與第三類艦船重疊嚴重，難以區(qū)分，且其分布不均勻，過多的離群值還可能對第一、二類艦船的識別造成影響。

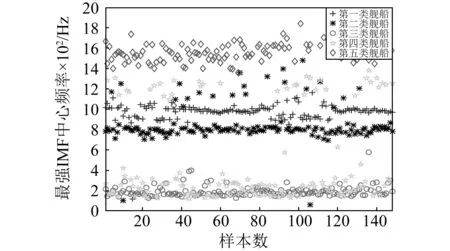
圖2 五類艦船輻射噪聲的最強IMF中心頻率

中心頻率第一類第二類第三類第四類第五類均值/Hz974.71842.31195.49466.191922.11標準差/Hz88.32177.3455.22434.62110.49

進一步，采取與文獻[7]相同的高頻(1 kHz～10 kHz)、低頻(0～1 kHz)以及能量定義，分析五類艦船輻射噪聲經(jīng)EEMD分解后各階IMF的高低頻能量差，結果如圖3、表2所示。可以發(fā)現(xiàn)，第二、三、四、五類艦船的高低頻能量差分布均勻，盡管第二、四類艦船的高低頻能量差均值接近，利用這一特征依然能較好區(qū)分兩類目標。但是，第一類艦船的高低頻能量差分布不均，且與第二、三、五類艦船的高低頻能量差特征存在重疊，不利于區(qū)分幾類目標。

圖3 五類艦船輻射噪聲的高低頻能量差

高低頻能量差第一類第二類第三類第四類第五類均值/dB-4.83-1.38-16.29-3.053.03標準差/dB6.9421.061.710.790.99

2.2 基于復雜度的特征提取

傳統(tǒng)的艦船輻射噪聲特征提取方法分析了信號的頻率、能量特征，本文則從復雜度的角度出發(fā)。首先提取五類艦船輻射噪聲的排列熵特征。由圖4和表3可知，五類艦船的排列熵特征分布均勻，表明了排列熵算法具有較強的穩(wěn)定性和一致性。由于五類艦船輻射噪聲的產(chǎn)生機理不同，其復雜程度理應存在差異，而排列熵很好地度量了這種差異。由平均排列熵值大小可見，第三類艦船的排列熵值最高，信號最復雜，隨后是第一、第五、第二和第四類。從排列熵特征分布來看，除第一與第五類艦船的排列熵特征分布略有重疊外，排列熵特征可以很好的區(qū)分五類艦船輻射噪聲。

圖4 五類艦船輻射噪聲的排列熵

排列熵第一類第二類第三類第四類第五類均值0.8520.7910.9250.7320.825標準差0.0230.0120.0060.0080.006

為了進一步提升排列熵特征的可區(qū)分性，引入多尺度排列熵從多個維度分析五類艦船輻射噪聲。五類艦船148個樣本在各尺度上的排列熵均值和標準差分別由圖5、表4和表5給出。從圖5和表5可以看出，五類艦船輻射噪聲在各個尺度上的排列熵分布均勻，離群值少，再次突顯了排列熵算法具有較強的穩(wěn)定性和一致性。此外，從圖5和表4還可以看出，盡管在某些尺度上，某幾類艦船的復雜程度相似，排列熵均值接近，但得益于多尺度排列熵的多維分析能力，每一類艦船都能在一些尺度上得到明顯區(qū)別于其他類艦船的熵特征，大大提升了艦船的可識別性。

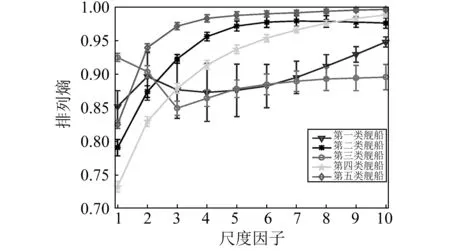
圖5 五類艦船輻射噪聲的多尺度排列熵

表4 五類艦船輻射噪聲的多尺度排列熵均值Tab.4 The average multi-scale permutation entropy of five types of ship radiated noise

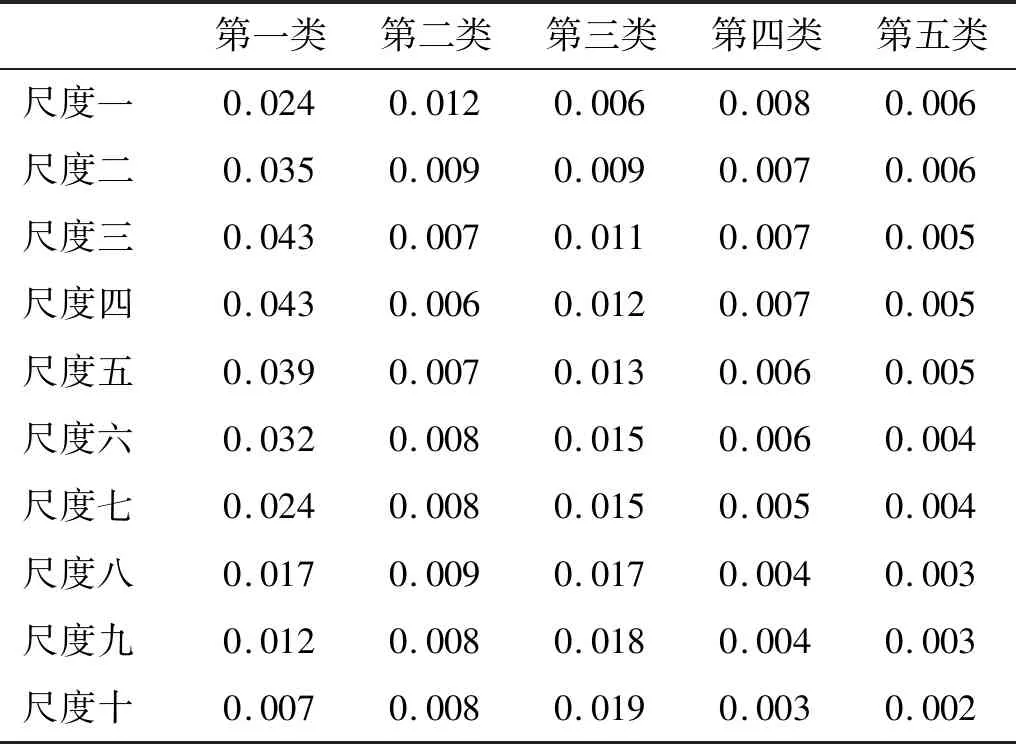
表5 五類艦船輻射噪聲的多尺度排列熵標準差Tab.5 The standard deviation of multi-scale permutation entropy for five types of ship radiated noise

3 模式識別

為了進一步比較幾種艦船輻射噪聲特征提取方法，引入概率神經(jīng)網(wǎng)絡[21]進行分類驗證。對每種特征提取算法，隨機選取每類艦船48個樣本作為訓練樣本進行分類器訓練，隨后利用每類艦船剩余的100個樣本作為測試樣本得到分類結果，詳細分類結果由表6～表9給出。

表6的分類結果與圖2的特征提取結果基本吻合，基于最強IMF中心頻率的特征提取對第一、三、五類艦船的識別率超過99%；而第二類艦船與第一類艦船的中心頻率特征接近，部分樣本被識別為第一類艦船，因此識別率稍低；特別地，由于第四類艦船的最強IMF中心頻率分布不均且與其他類別艦船特征存在重疊，神經(jīng)網(wǎng)絡分類器無法對其進行識別，識別率為0。類似的，表7的分類結果與圖3的特征提取結果相吻合，由于第一類艦船的高低頻能量差特征分布不均，分類器無法對其識別，識別率為0；第二與第四類艦船的高低頻能量差特征相近，因此識別率分別為69%和84%；第三與第五類艦船的高低頻能量差特征可區(qū)分性強，識別率高于99%。總體來說，基于EEMD的特征提取方法識別率高于70%，與文獻[8]的研究結果相同，最強IMF中心頻率特征要優(yōu)于高低頻能量差特征。

表8的分類結果與圖4的排列熵特征提取結果吻合，基于排列熵的艦船輻射噪聲特征提取方法對第三、四、五類艦船的識別率達到100%；由于第一、二、五類艦船的排列熵特征略有重疊，因此分別有50個和17個第一類和第二類艦船被識別為第五類。盡管如此，排列熵的總體識別率依然高達85.2%，優(yōu)于基于EEMD的特征提取方法。表9為基于多尺度排列熵的分類結果，由于可以從多個維度描述信號，因此，多尺度排列熵對每類艦船都有較好的識別率，總體識別率高達95.8%，顯著高于只能從單個尺度描述信號的基于EEMD的特征提取方法和基于單尺度排列熵的特征提取方法。

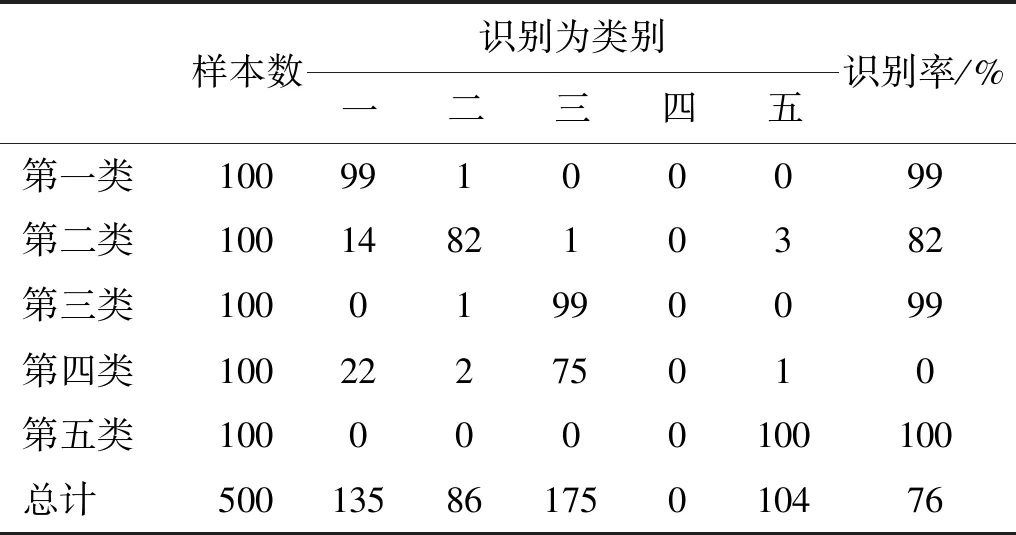
表6 基于最強IMF中心頻率的概率神經(jīng)網(wǎng)絡分類結果Tab.6 The PNN identification results based on the center frequency of IMF with the highest energy

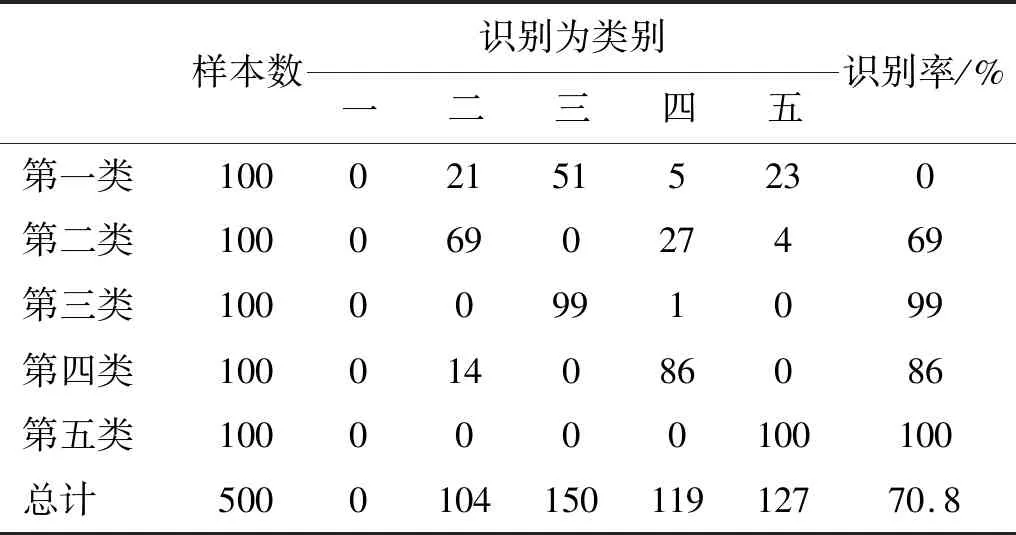
表7 基于高低頻能量差的概率神經(jīng)網(wǎng)絡分類結果Tab.7 The PNN identification results based on the energy difference between high and low frequency

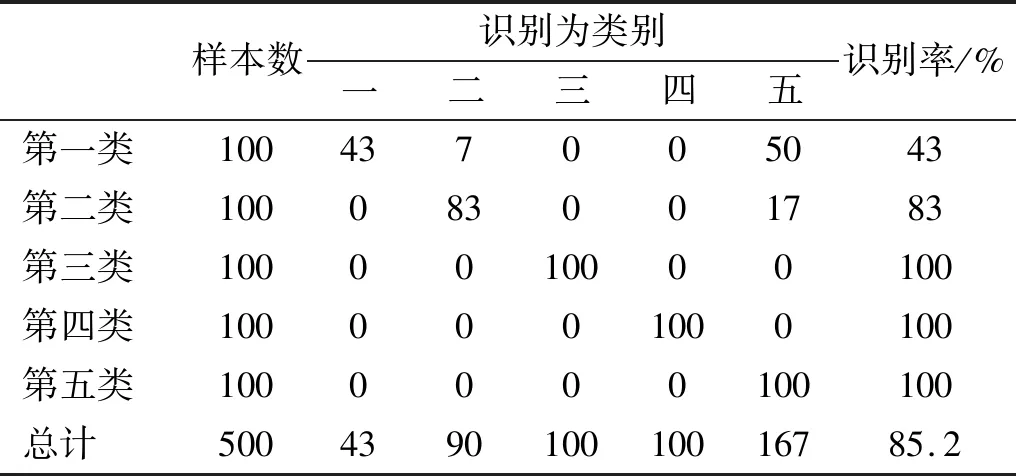
表8 基于排列熵的概率神經(jīng)網(wǎng)絡分類結果Tab.8 The PNN identification results based on permutation entropy

表9 基于多尺度排列熵的概率神經(jīng)網(wǎng)絡分類結果Tab.9 The PNN identification results based on multi-scale permutation entropy

4 結 論

本文提出一種基于多尺度排列熵的艦船輻射噪聲特征提取方法，從復雜度的角度研究艦船輻射噪聲，通過實測艦船輻射噪聲特征提取和分類識別實驗表明：

(1)不同類別艦船輻射噪聲的產(chǎn)生機理不同，其復雜程度存在差異，復雜度特征是一種有效的艦船識別特征。

(2)多尺度排列熵只需要較短數(shù)據(jù)(0.2 s)就能獲得穩(wěn)定的熵值，是一種穩(wěn)定性強、一致性好的復雜度特征提取方法。

(3)多尺度排列熵可以從多個維度描述艦船輻射噪聲，具有很強的可分性。以多尺度排列熵為特征的分類識別效果顯著優(yōu)于只能從單個尺度描述信號的基于EEMD的特征提取方法和基于單尺度排列熵的特征提取方法。