考慮尺度效應的微振動能量采集器建模

李創業， 霍 睿， 王偉科， 趙 辰

(1. 山東大學 機械工程學院，濟南 250061； 2. 山東大學 高效潔靜機械制造教育部重點實驗室, 山東 濟南 250061；3. 中國人民解放軍32145部隊 機要科, 河南 新鄉 453000)

“物聯網”[2-4]囊括了數以萬計的傳感器，傳統供電方式因壽命短、儲能有限、更換費用昂貴、污染環境等缺點[5]無法滿足物聯網持久、可集成、工作環境多變、環境友好型的供能需求，新型1供電技術的研究意義重大。壓電式能量采集器[6]可以將機械能吸收轉化為電能，具備能量轉化效率高、結構簡單緊湊、壽命長、環境友好、與微納制造技術兼容等優勢[7]。由于尺度效應，微結構力學性能與宏觀模型分析結果不吻合[8-10]。而微壓電懸臂梁是微振動能量采集器的一種基本結構形式。

基于此，本文首先驗證了考慮尺度效應的懸臂梁模型，進而建立微振動能量采集器的改進模型。通過仿真和實驗證明本文建立的采集器改進模型有效的降低了誤差。改進模型為微供能設備的設計提供了參考依據。

1 微壓電懸臂梁模型改進及驗證

1.1 微壓電懸臂梁動力學模型

不考慮尺度效應，微梁動力學模型是

(1)

文獻[11]中引入表征尺寸效應的本征長度l，采用偶應力理論改進了微梁的動力學模型，得到運動控制方程如下

(2)

式中：h為微梁厚度，無量綱厚度h/l=3.5。根據振型疊加法，可以得到諧振頻率

(3)

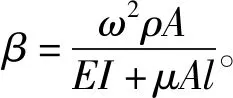
1.2 微壓電懸臂梁有限元分析

由式(2)可知：在尺度效應影響下，μAl2是微懸臂梁剛度增大[12-15]的主要原因，為便于進行有限元分析，引入等效楊氏模量E1

(4)

微懸臂梁可簡化為Si梁和PZT-5H兩層結構。簡化后Si的尺寸LSi×WSi×TSi：3 150 μm×1 000 μm×13 μm；PZT-5H的尺寸LPZT-5H×WPZT-5H×TPZT-5H：3 150 μm×1 000 μm×1.6 μm。引用文獻[16]中的參數，結合式(4)可得等效楊氏模量，如表1所示。

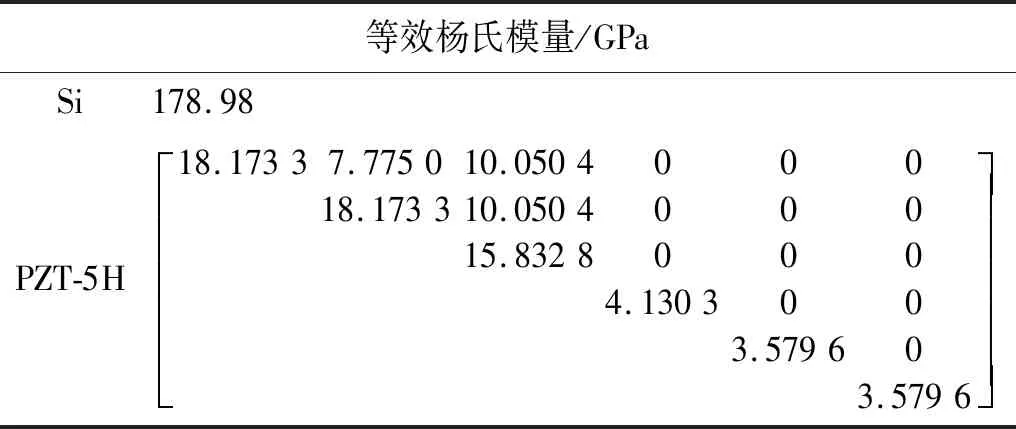
表1 材料的等效楊氏模量

對懸臂梁進行有限元分析，得到懸臂梁宏觀與改進模型的一階振型圖，模態頻率分別為1 536 Hz與1 803 Hz。如圖1和圖2所示。

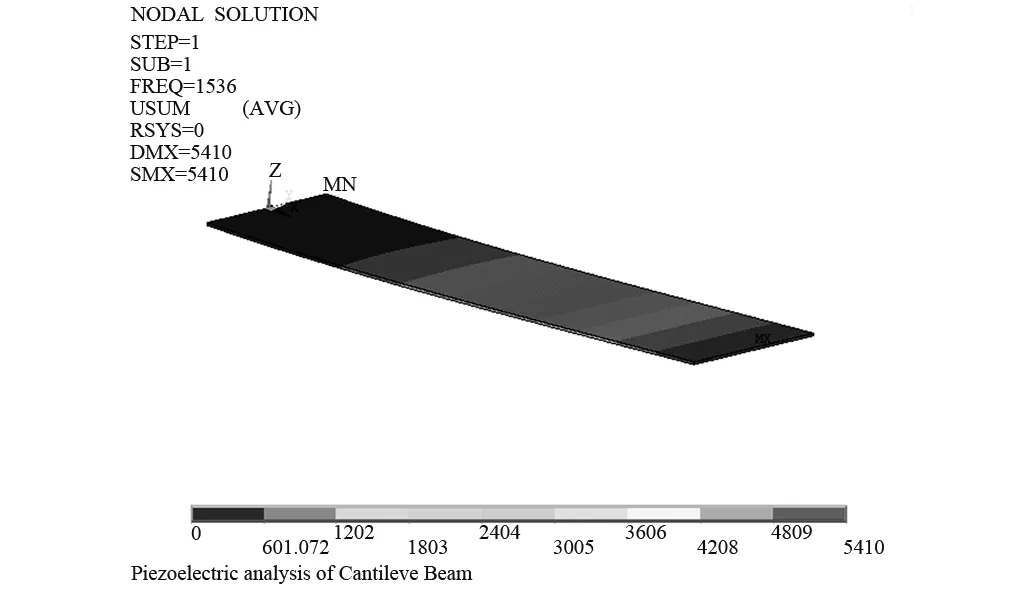
圖1 懸臂梁宏觀理論模型有限元分析結果

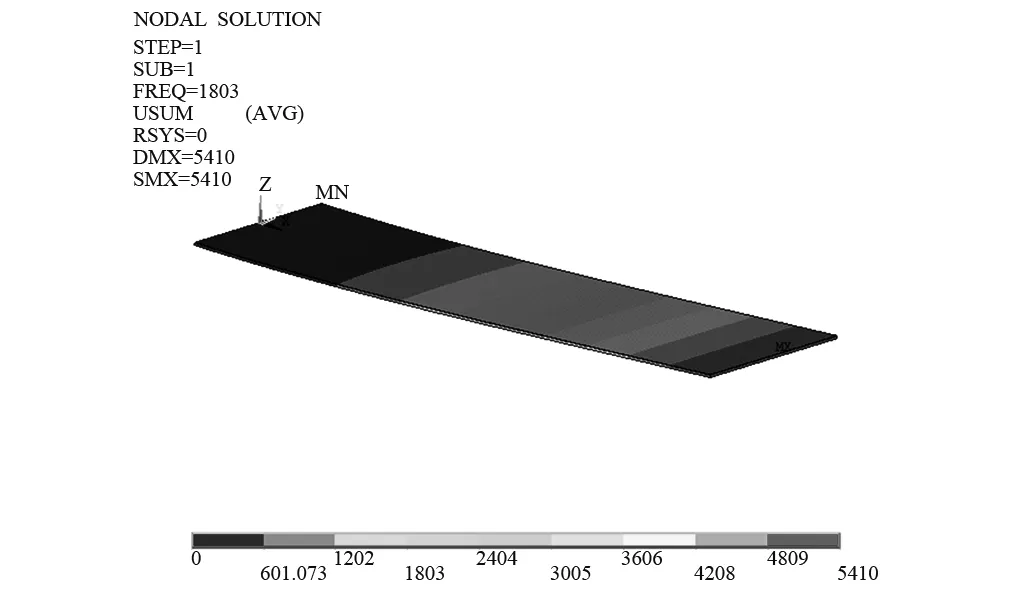
圖2 懸臂梁改進理論模型有限元分析結果

1.3 微壓電懸臂梁制作與性能測試

在4 10.16 cm的SOI基片上采用光刻、濺射、溶膠凝膠、干法刻蝕等工藝完成制備與封裝，其SEM圖，如圖3和4所示。

圖3 微壓電懸臂梁俯視圖

圖4 微壓電懸臂梁厚度放大圖

采用信號發生器(YE1311)、功率放大器(E5871A)、振動臺(E-JZK-5)、激光測振儀(OFV505/5000)、數據采集卡(INTEST Main Unit INJ9008U-I)、加速度傳感器(CA-YD-1182)等儀器搭建了如圖5所示的懸臂梁振動特性實驗平臺。

圖5 實驗平臺

當加速度激勵為6 g(1 g=9.8 m/s2)時，在1 600～2 000 Hz范圍內依次改變振動加速度的頻率，并記錄尖端位移的數據。采用功率譜對尖端位移進行處理，可得到功率譜值與振動頻率的曲線，如圖6所示。在1 818 Hz時，功率譜值達到最大，即為諧振頻率。

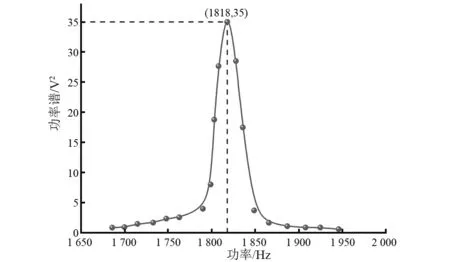
圖6 尖端位移曲線的功率譜-頻率曲線

由表2可知，宏觀理論模型與實驗測試的諧振頻率相差282 Hz，誤差是15.5%；而考慮尺度效應后，改進理論模型與實測結果相差15 Hz，誤差是0.8%；

表2 實驗測試頻率和理論分析頻率對比

2 微壓電振動能量采集器建模及驗證

由上一小節知，微梁的諧振頻率在1 000 Hz以上，然而傳感器周圍環境中的低頻振動較多。大量學者[17-19]通過在懸臂梁自由端附加Si或Ni質量塊來減小諧振頻率，使其能在低頻振動環境中發揮作用。本文把Si質量塊刻蝕到T型懸臂梁上，得到了“T型”采集器，采集器可簡化為由PZT-5H、Si梁和質量塊三層結構組成[20]。結構如圖7所示。

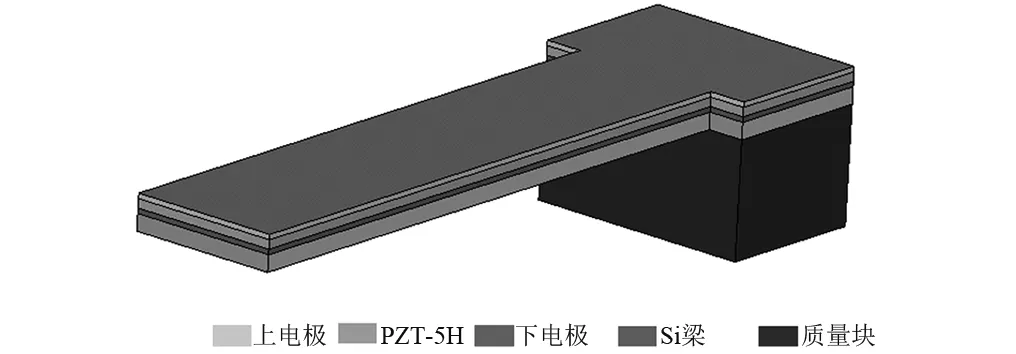
圖7 T型采集器結構示意圖

2.1 微振動能量采集器動力學模型

考慮尺度效應，并結合微梁的改進理論模型，采集器自由振動的動力學模型為

(5)

當除去式(5)中的μAl2時，模型自動退化為宏觀理論模型。在給定的邊界條件下，設諧振頻率為ωr，振型函數為Wr(x)，第r階模態質量Mr。引進正則坐標qr(t)，根據振型疊加原理，對微分方程解耦，可得

(6)

采集器形變產生的電荷Q集聚在PZT-5H的上下表面，形成電容器，容易得出

(7)

式中：Ss為極板正對的面積；εr為相對介電常數；Cs為等效電容。Vs是PZT-5H上、下表面之間的電勢差，也是微振動能量采集器的開路輸出電壓。

2.2 微振動能量采集器有限元分析

有限元分析結果以云圖的形式可以體現出采集器的實際運動狀態。沿用表1中的等效彈性模量及文獻[16]中相關參數，建立采集器有限元模型。設置固定端的自由度為零，加載幅值為1 g加速度激勵后，輸出電壓和尖端位移在諧振頻率300 Hz處均到達最大，輸出電壓為0.17 V，尖端位移為10.7 μm。

2.3 微振動能量采集器性能測試

設定加速度激勵幅值為1 g，采用確定頻率激勵方式在50～500 Hz范圍內對振動臺進行激振，并在PC端觀測記錄加速度、自由端的尖端位移與輸出電壓。

圖8、圖9給出了采集器分別由宏觀模型、改進模型以及實驗測試所得的尖端位移-頻率曲線、輸出電壓-頻率曲線。各諧振點上的主要信息以及與實驗結果的對比誤差詳見表3。

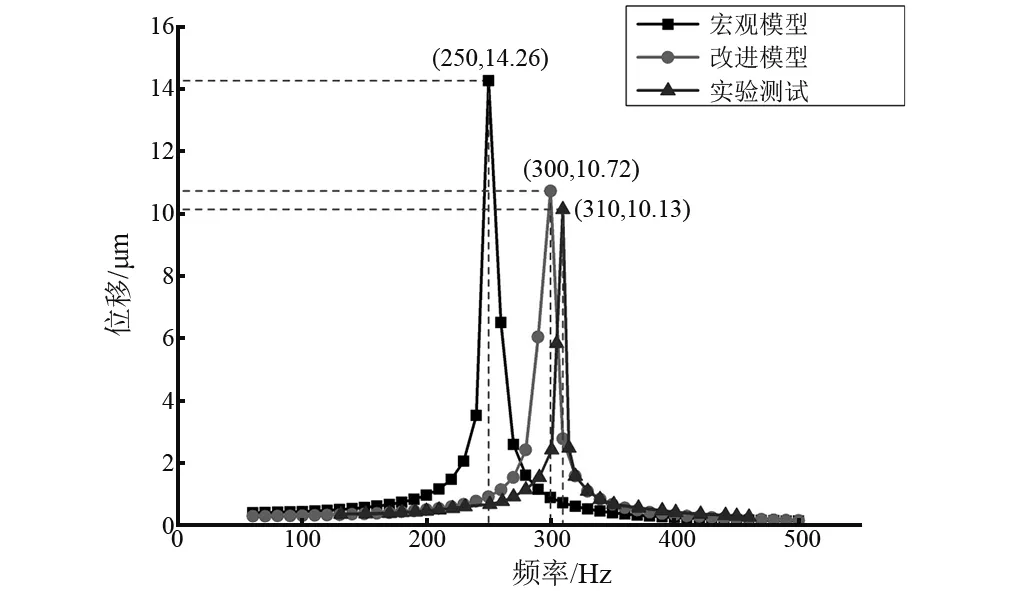
圖8 微振動能量采集器的位移-頻率曲線

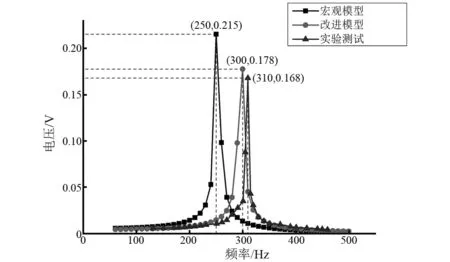
圖9 微振動能量采集器的電壓-頻率曲線

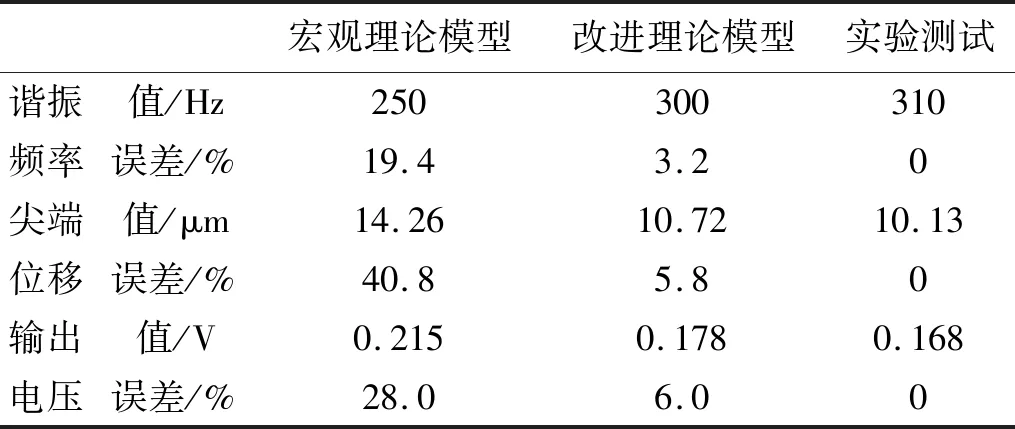
宏觀理論模型改進理論模型實驗測試諧振值/Hz250300310頻率誤差/%19.43.20尖端值/μm14.2610.7210.13位移誤差/%40.85.80輸出值/V0.2150.1780.168電壓誤差/%28.06.00

宏觀理論模型分析與實驗測試獲得的諧振頻率之間誤差為19.4%，尖端位移誤差為40.8%，輸出電壓誤差為28%，宏觀模型無法準確描述微振動能量采集器的動力學性能；改進理論模型分析與實驗測試兩種方式獲得的諧振頻率之間誤差為3.2%，尖端位移誤差為5.8%，輸出電壓的誤差為6.0%，改進模型分析的結果與實驗結果吻合較好，但仍有一定誤差。

3 誤差影響因素分析

理論計算與實際測試結果之間的偏差，可由兩方面的因素導致：一是在理論模型中存在一些近似假設，例如Euler梁[21]假設，一是計算參數不夠精確。

在理論建模方面，如前所述，尺度效應是理論模型誤差的一個重要來源，此外應考慮其他理論假設因素的影響。由于本文理論計算是基于有限元模型，在建模方法上是將壓電層和Si基梁分別劃分相同數量的單元，在兩種材料的結合面上令其對應單元節點合二為一，其中即考慮了材料剪切作用的影響，因此可以認為理論模型本身有較高的計算精度。

由于微器件的加工制作公差，使計算參數不夠精確，不可避免地造成理論計算與實際測試結果之間的偏差。以下僅以式(1)的Euler梁模型對加工公差造成的計算誤差進行簡要分析。在此采用Euler梁模型一方面是為簡化理論計算，一方面注意到對于本文算例，壓電層的厚度遠小于Si基梁，PZT-5H的楊氏模量也遠小于Si，按設計尺寸，可估算壓電層與Si基梁的抗彎剛度之比約為5.2×105。

在式(3)中令r=1，并注意到β1L=1.875以及對矩形截面I=Ah2/12，同時引用式(4)的等效楊氏模量，有

(8)

顯然，根據式(8)，微梁寬度誤差不對其基頻產生影響。假設微梁的長度存在加工誤差ΔL，則由其導致基頻計算誤差

(9)

取式(9)與式(8)的比值

(10)

亦即每1%的長度加工誤差將導致約2%的固有頻率計算誤差。類似地可知，每1%的厚度加工誤差將產生相同比率的固有頻率計算誤差。此外，設若材料密度取值與實際值存在1%的偏差，則導致固有頻率計算產生約0.5%的誤差。最后，基于Euler梁理論也可對尺度效應造成的固有頻率計算誤差進行大致估計

(11)

對本文算例，式(11)計算結果約為18.8%，對比表2的宏觀理論模型誤差大致相當；上式計算結果偏大的主要原因，可解釋為ΔE1較大，因而需要考慮泰勒級數的高階項以提高誤差估計精度。

4 結 論

本文以微壓電懸臂梁為研究對象，研究了尺度效應對微結構力學性能的影響，引入材料的本征長度，采用改進的偶應力理論完善了動力學模型。通過有限元分析與實驗測試的方式研究了微壓電懸臂梁的力學性能，表明改進模型精度更高。以微梁力學性能研究結果為基礎，改進了微振動能量采集器的動力學模型，采用有限元方法和實驗測試分析采集器的輸出性能。改進的采集器動力學模型可以更好的解釋尺度效應對微結構力學性能的影響。