不同變槳控制對海上風力機漂浮穩定性影響研究

余 萬， 丁勤衛， 李 春,2， 郝文星， 周紅杰， 朱海天， 韓志偉

(1. 上海理工大學 能源與動力工程學院，上海 200093；2. 上海市動力工程多相流動與傳熱重點實驗室，上海 200093)

風力機運行調節方式主要有定槳失速調節和變槳調節[1]。對于定槳失速調節，葉片與輪轂固定連接即槳距角固定不變，當風速變化時，風力機通過葉片翼型自身失速特性(升阻比的下降)以限制功率輸出。變槳調節主要在兩個風速段實現調節：①小于額定風速：葉片保持最優槳距角不變且通過調節發電機電磁轉矩達到調節風輪轉速，最終實現風力機在最佳尖速比下運行，以獲得最大風能利用系數，輸出最大功率；②大于額定風速：風力機通過改變槳距角且保持風輪轉速不變，即改變風能利用系數以保持發電機以額定功率輸出。變槳調節較之定槳失速調節，不僅能使得風力機處于最優運行狀態且最大程度上提高發電效率，還可避免失速調節帶來的機組運行不穩定和傳動機構及葉片承受大扭矩和高應力的情況[2]。因此，現代大型化風力機通常采用變槳調節[3]。對于大型化風力機變槳控制調節的研究很多且相對應的技術較為成熟，不同研究成果均表明基于現代理論的干擾自適應控制(Disturbance Accommodating Control，DAC)較之傳統比例積分控制(Proportional Integral Control，PIC)有著更好的控制性能[4-7]。

隨著陸上風力機建設趨于飽和，漂浮式風力機為開發利用深海區域低湍流度且更為豐富的風能資源提供一種可行的辦法。為此，風電場的建設業已成“由陸向海，由深向淺，由固定式向漂浮式”的必然趨勢[8-10]。2009年6月，世界上第一個基于Spar平臺的海上漂浮式風力機在挪威海深220 m區域安裝成功[11]。目前，關于風力機變槳控制對漂浮式風力機平臺動態響應影響的研究較少。Namik等[12-13]考慮湍流風及波浪載荷作用，設計狀態空間變槳控制器及干擾自適應控制器，對比分析不同控制器對駁船式、張力腿式及Spar式三種不同漂浮式風力機的影響，但對于漂浮式風力機平臺動態性能影響分析過于簡單。Bagherieh等[14]采用線性參數時變控制方法(Linear Parameter Varying Control，LPVC)，研究基于駁船式平臺的漂浮式風力機在有無LPVC控制下的輸出功率及運動性能，但控制效果不明顯且對于駁船式平臺運動分析簡單。

海上漂浮式風力機(下簡稱海上風力機)與陸上風力機結構動態特性的最大區別為，前者具有漂浮特性即平臺動態特性，同時海上風力機的漂浮穩定性是影響其獲取深海區域風能的重要因素[15]。海上風力機葉片不同的變槳控制策略將會影響支撐平臺的動態響應。因此，本文考慮湍流風及不規則波浪的作用，在Matlab/Simulink與開源軟件FAST聯合仿真平臺上，設計干擾自適應控制器(DAC)，并與FAST原有的控制策略對比分析，研究不同控制器對海上風力機漂浮穩定性影響。研究結果以期為設計更適合海上風力機的變槳控制器提供理論基礎。

1 仿真模型

1.1 海上風力機主要參數

研究對象為基于Spar浮式基礎海上風力機。風力機選用美國國家可再生能源實驗室(National Renewable Energy Laboratory，NREL)的5 MW風力機樣機，主要參數如表1所示；Spar浮式基礎選用OC3-Hywind Spar平臺，主要參數，如表2所示。

在環境載荷作用下，漂浮式Spar平臺將會產生六個自由度方向的運動[18]。平動自由度：縱蕩、橫蕩及垂蕩；轉動自由度：橫搖、縱搖及艏搖，如圖1所示。圖中，X軸表示為風輪平面法向方向，βw為波浪入射角。

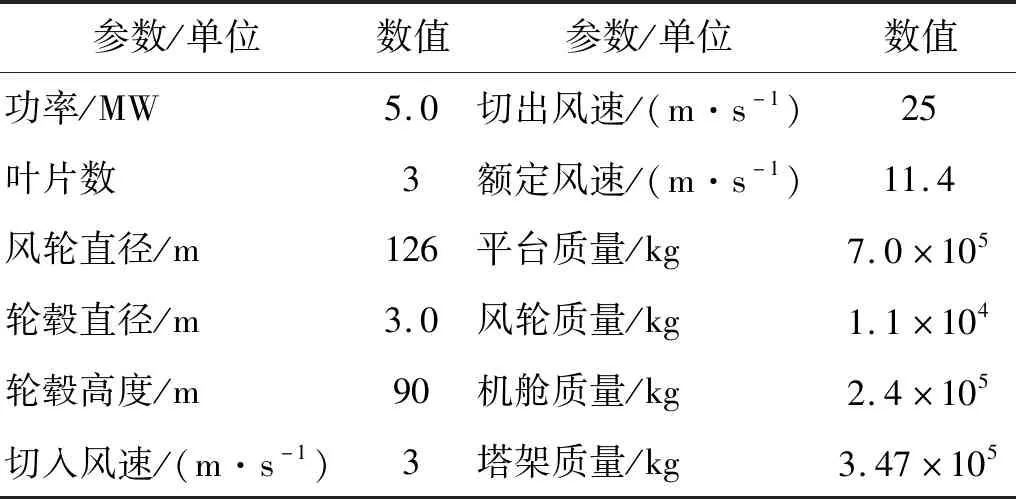
表1 NREL 5 MW 風力機樣機主要參數[16]

表2 OC3-Hywind Spar平臺參數[17]

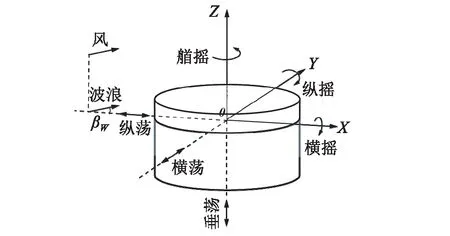
圖1 平臺運動自由度

1.2 風力機系統模型[5]

NREL 5 MW 風力機樣機主要部件有：風輪、低速軸、變速箱、高速軸及發電機。其中，風輪是捕獲風能的唯一部件，其獲取能量的計算表達式為：

Pw=0.5ρπR2Cp(λ,β)v3

(1)

式中：ρ為空氣密度；v為風速；R為風輪半徑；Cp(λ,β)為風能利用系數，與槳距角β及尖速比λ有著非線性函數關系。

尖速比λ表達式為：

λ=ΩrR/v

(2)

式中：Ωr為風輪轉速。

風輪氣動力矩表達式為：

Tr=0.5πρR3v2Cp(λ,β)/λ

(3)

考慮低速軸為剛性體，則風輪及發電機的運動方程分別為：

(4)

(5)

式中：Jr及Jg分別為風輪及發電機轉動慣量；Ωg為發電機轉速；Tl、Th及Te分別為低速軸力矩、高速軸力矩及發電機電磁轉矩；Cr及Cg分別為風輪及發電機外部阻尼。

變速箱的傳動比為：

ng=Tl/Th=Ωg/Ωr

(6)

將方程(6)代入方程(4)和(5)得到風力機系統運動方程表達式：

(7)

1.3 風力機線性模型

開源軟件FAST提供兩種風力機非線性氣動彈性的線性模型：符號法和數值攝動法。由于數值攝動法考慮了氣動力的影響，故采用該方法建立風力機的線性模型。線性模型的建立步驟為：①在周期性穩態風下，FAST計算得到穩態結果；②針對運動方程中每個自由度引入數值攝動，構建偏微分方程；③求解偏微分方程可得到包含質量、剛度及阻尼矩陣的各種系數[19]。風力機的線性模型可描述為：

(8)

式中：x為狀態向量；u為控制輸入；ud為風擾動輸入；y為輸出向量；A為狀態矩陣；B為控制輸入矩陣；Bd為風擾動輸入矩陣；C為輸出狀態矩陣；D為控制輸入傳輸矩陣；Dd是風擾動輸入傳輸矩陣。

2 風力機運行控制

2.1 運行控制原理

變速變槳風力機主要有三個運行區域，如圖2所示：在區域1，風速小于風力機切入風速，風力機輸出功率為零；在區域2，風速大于風力機切入風速，小于其額定風速，風力機控制目標是跟蹤最優尖速比，獲得最高的風能利用系數，輸出最大功率；在區域3，風速大于風力機額定風速，小于其切出風速，風力機控制目標是跟蹤其額定輸出功率。

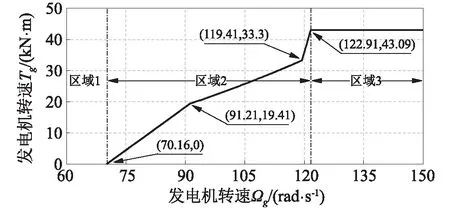
圖2 風力機運行區域

對于風力機的運行控制策略主要有區域2及區域3。當風速小于額定風速即區域2時，通過控制發電機的轉矩使風力機獲取最多的能量，輸出最大功率；當風速大于額定風速即區域3時，風力機通過改變葉片槳距角使得來流攻角產生變化，進而改變葉片風能利用系數，最終可控制風力機輸出功率。

風力發電機轉矩控制不屬于重點研究內容，故根據FAST定義如圖2所示的曲線圖進行給定，曲線函數定義為：

(9)

風力機大于額定風速的葉片變槳控制作為重點研究對象。設計干擾自適應控制器，并應用于海上風力機運行區域3。FAST在對風力機系統線性化時需要設定穩態點，本文選擇的穩態點為風速18 m/s、風輪轉速12.1 r/min及槳距角為14.74°。

2.2 FAST控制策略

在運行區域3的控制目標是通過葉片的槳距角變化以維持風輪轉速在穩態點風輪轉速。FAST控制采用傳統PI控制，對應著單輸入單輸出的情況。將其與穩態值的偏差作為輸入，故槳距角變化量可定義為：

(10)

式中：δβ為槳距角偏差；Kp、Ki及KD分別為比例、積分及微分系數；δΩr為風輪轉速的偏差。

通過開源軟件FAST對穩態點進行線性化模擬，可得到：

(11)

式中：δv為風力機輪轂高度處的風速擾動量。

將方程(10)代入方程(11)同時在Laplace變換域內變換，可得到PI控制系統的傳遞函數為：

(12)

對于具有穩定性的閉環系統，傳遞函數的分母項的根位于復平面的左側即有負實部的根，因此要求分母項各系數項都大于零：

(13)

將傳遞函數分母轉換為一般形式可得：

s2+2δωs+ω2=0

(14)

式中，ω為頻率；δ為阻尼比；δ和ω表達式為：

(15)

根據方程(15)可求得Ki及Kp表達式為：

(16)

在高風速區域，槳距角的微小的變化將會導致轉矩產生很大波動。通常采用控制器增益調度技術用于補償轉矩這種波動，增益調度系數GK定義為：

(17)

式中：β為槳距角；KK為常數，在FAST控制策略中取為0.109 965。

圖3為依據FAST控制策略搭建的PI控制Simulink模型。

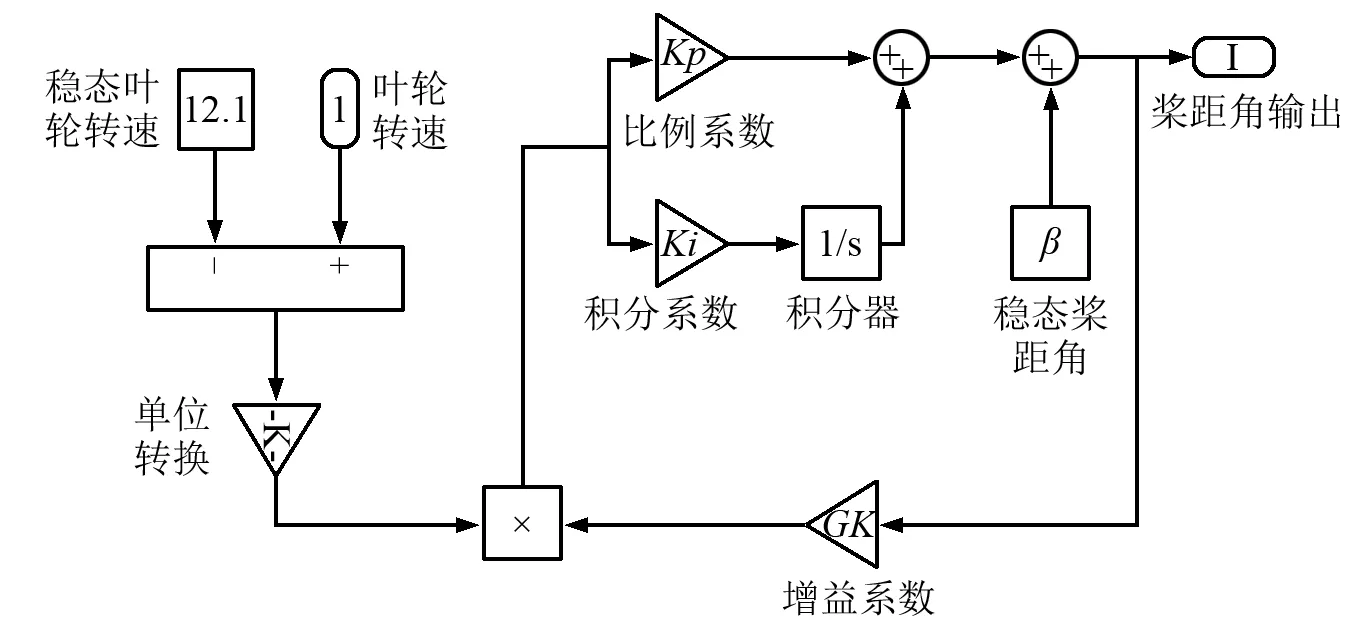
圖3 FAST的Simulink模型(KD=0)

在Simulink模型中，根據風力機輸出某一時刻的風輪轉速并與穩態點風輪轉速及增益系數的關系可以得到系統輸入偏差，且通過比例及積分系數可獲得系統輸出偏差即槳距角偏差值，最終可得到該時刻的槳距角。在FAST控制策略中，比例系數為0.608 68，積分系數為0.086 962。

2.3 干擾自適應控制

2.3.1 全狀態反饋控制

在風力機線性模型中對控制輸入u構建反饋法則：

u=Gx

(18)

則開環系統與反饋法則所構成閉環系統方程為(忽略擾動輸入)：

(19)

閉環系統的穩定性取決于反饋矩陣G的確定。在閉環系統中，可通過系統的極點配置即矩陣A+BG特征值的設定從而選擇反饋矩陣G。對于控制系統具有可控性即矩陣A和B滿足方程(20)時，閉環系統的極點可任意配置。

Rank[B∶AB∶A2B∶…∶An-1B]=n

(20)

在風力機的控制設計中，極點配置對系統有極大的影響。當極點的實部位于復平面的左側不僅可調節風輪轉速或者風力機輸出功率，還可對低阻尼的柔性振動提供額外阻尼。

圖4為全反饋控制器示意圖。在風力機的控制過程中，全狀態反饋要求能夠測量得到控制系統中所有狀態在工程實際中很難實現。為此，在風力機的控制系統中需要通過狀態觀測器估計狀態量。

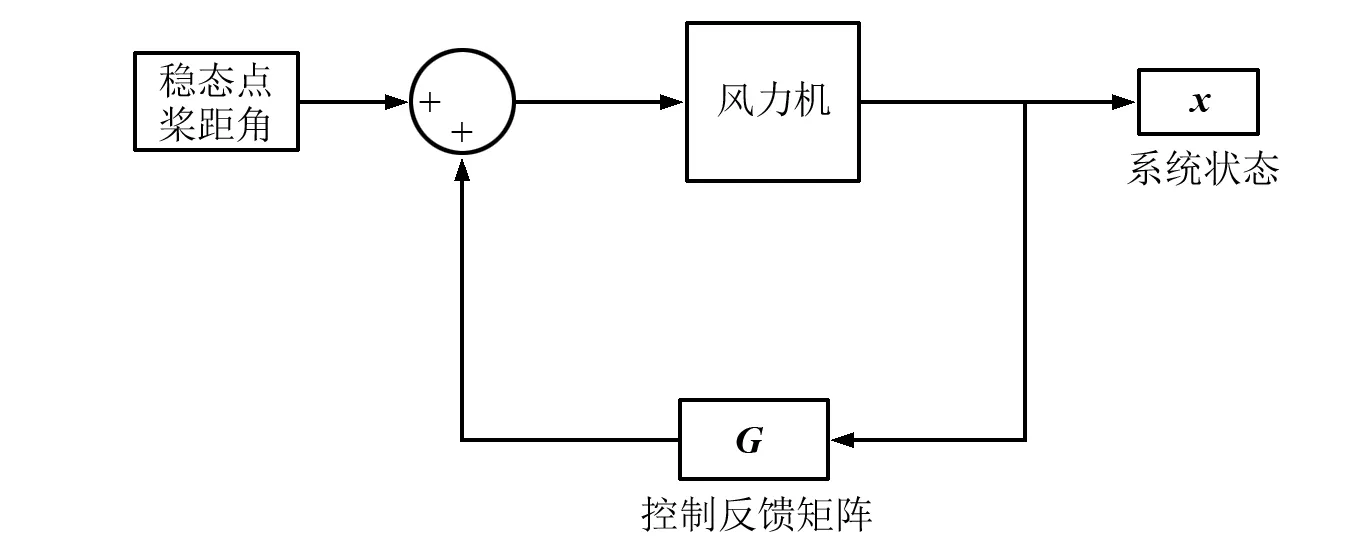
圖4 全反饋控制器示意圖

風力機輸出某一時刻系統狀態量，根據控制反饋矩陣即可求得槳距角的偏差值。

2.3.2 狀態觀測器

狀態觀測器以全反饋控制為基礎且通過系統空間狀態模型輸出估計的系統狀態。忽略擾動量，狀態觀測器數學模型為：

(21)

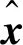
實際系統狀態與系統狀態估計值之間的誤差可表示為：

(22)

對狀態誤差求導可表示為：

(23)

對于矩陣Kx采用與反饋矩陣G的相同求解方法。不同得是需要判斷系統是否具有可觀性，即矩陣A和C滿足方程(24)時，極點可任意配置即對于矩陣A-KxC的特征量可任意設定。

(24)

具有狀態觀測器的全狀態反饋控制，如圖5所示。

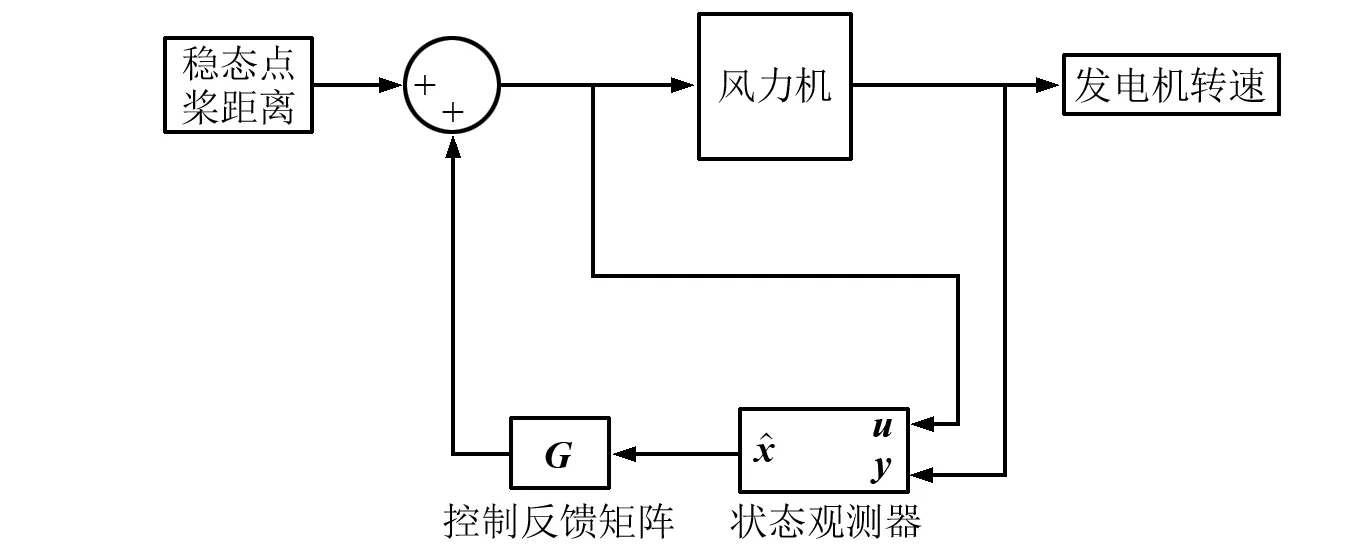
圖5 狀態觀測器控制示意圖

考慮到風力機系統中各個系統狀態量在工程上測量難以實現。因此，采用易測量的狀態值，并利用狀態觀測器估計系統各個狀態量，再根據控制反饋矩陣可求得槳距角的偏差值。

2.3.3 干擾自適應控制

在風力機運行過程中，湍流風會引起葉片的氣動力波動從而影響風力機的輸出功率、扭矩及其載荷[20]。為此，基于全狀態反饋控制及狀態觀測器控制實現干擾自適應控制。干擾自適應控制通過干擾波模型構建擾動狀態；擾動狀態用于狀態反饋中以減小或抵消擾動作用。干擾波模型發生器設計為：

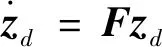
(25)

式中：zd為干擾狀態；F和θ為根據干擾特性確定的已知矩陣，本文選取及。

在全狀態反饋的基礎上，考慮干擾狀態，構建反饋法則為：

u=Gx+Ddzd

(26)

將方程(26)代入全狀態反饋控制(考慮擾動輸入)可得：

(27)

狀態反饋中擾動狀態作用為減小或抵消干擾作用，故要求min(BGd+Bdθ)最小，則可得到Gd。

在干擾自適應控制中構建的干擾狀態與全狀態反饋控制中系統狀態相同，需要基于狀態觀測器估計干擾狀態。采用干擾自適應控制的基于狀態觀測器的全狀態反饋控制器數學模型為：

(28)

狀態估計值與實際狀態值之間的誤差為：

(29)

與方程(29)同理，可得估計誤差的狀態方程：

(30)

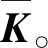
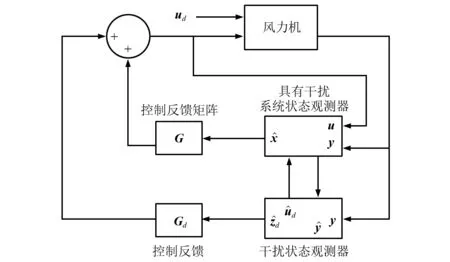
圖6 干擾自適應控制示意圖

為考慮風擾動作用，故將風擾動輸入作為一個系統狀態量，并采用干擾狀態觀測器評估該狀態量，再通過反饋矩陣求解得到槳距角的偏差值。

4 結果與分析

選取平均風速18 m/s的湍流風，風速時間曲線如圖7(a)所示。波浪譜選取P-M譜，有義波高為3.673 m，跨零周期為13.376 s，波浪入流角度為0°，波浪高度時間曲線如圖7(b)所示。

在以上載荷激勵下，采用DAC對海上風力機葉片槳距角控制，并與FAST所采用的PI控制策略進行對比分析。

4.1 海上風力機控制效果分析

在DAC及FAST控制策略下，海上風力機控制效果如圖8所示。其中，圖8(a)為兩種控制策略下槳距角曲線圖；圖8(b)為對應控制策略下風力機風輪轉速曲線圖；圖8(c)為風力機輸出功率曲線圖。

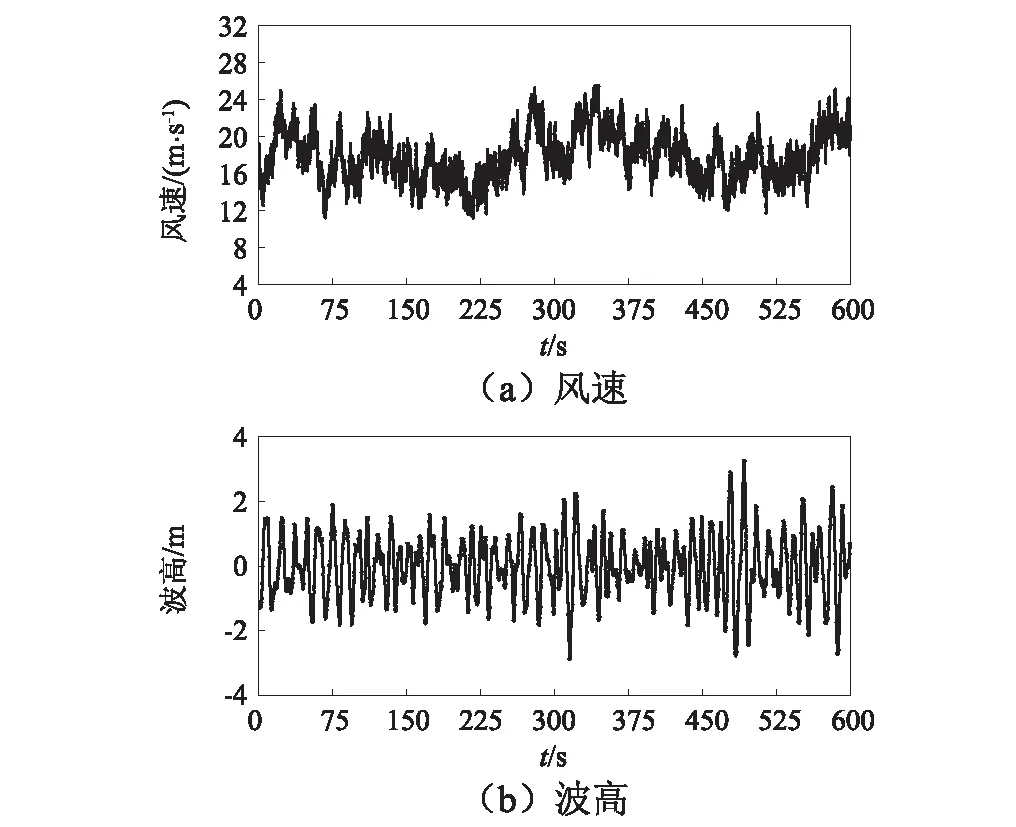
圖7 風和波浪曲線

由圖8可知，FAST控制策略槳距角曲線波動最小，其控制得到的風輪轉速及輸出功率控制得到的波動較大；DAC槳距角波動大，其控制得到的風輪轉速及輸出功率波動最小。表3為不同控制策略下海上風力機槳距角、風輪轉速及輸出功率均方根及標準差。

根據表3可知，FAST控制策略得到的槳距角、風輪轉速及輸出功率均方根與穩態值相對誤差分別為-0.875%、0.413%及-6.930%，DAC控制策略得到的相對誤差分別為-2.354%、-0.165%及-2.795%；在DAC控制策略下的槳距角、風輪轉速及輸出功率的標準差與FAST控制策略相對誤差分別為36.117%、-56.432%及-44.066%。因此，盡管DAC較之于FAST得到的槳距角與穩態值相對誤差較大，標準差大，但DAC因其具有盡快適應風速的變化的特點使海上風力機風輪轉速波動更小，輸出功率更加穩定，故對海上風力機的控制效果更好。

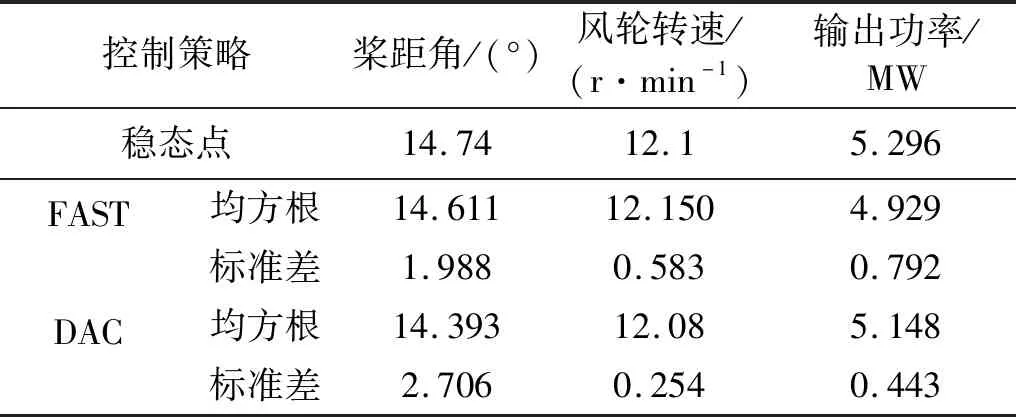
表3 不同控制策略下統計參數

4.2 海上風力機漂浮穩定性時域分析

較之陸上風力機，海上風力機的漂浮穩定性是影響開發利用深海區域風能的重要因素。海上風力機在區域3內變槳控制會導致系統結構上部風輪所受載荷發生變化，此將會進一步影響其結構下端漂浮式平臺動態響應，即海上風力機漂浮穩定性隨之變化。因此，在開發風力機控制策略必須考慮其對于海上風力機漂浮穩定性的影響，從而達到既能保持以額定功率輸出，又可提高平臺穩定性的目的。圖9為兩種不同控制策略下海上風力機支撐平臺六個自由度動態響應曲線圖；曲線圖左下角三維坐標標記對應著自由度方向，例如在平動自由度縱蕩方向上，平行于實線X軸的雙箭頭直線表明其沿軸做平動運動；在轉動自由度橫搖中，垂直于實線X軸的雙箭頭直線表明其繞軸做轉動運動。

圖8 海上風力機控制效果圖

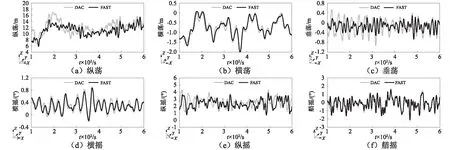
圖9 平臺動態響應

由圖9可知，在縱蕩方向上，由于風及波浪作用，平臺會產生很大的動態響應，在FAST控制策略下，動態響應具有較小的波動，在DAC控制策略下有著較大的波動；在橫蕩方向上，對比兩種控制策略，動態響應曲線差別較小；在垂蕩方向上，較之FAST，DAC控制策略下的動態響應較大；在橫搖方向上，兩種控制策略下的動態響應曲線差別較小；在縱搖方向上，較之于FAST，DAC控制策略下的動態響應較大；在艏搖方向上，兩種控制策略得到的動態響應曲線差別不明顯。進一步定量分析海上風力機漂浮穩定性，給出如圖10所示的不同控制策略下平臺各自由度動態響應的均方根及標準差。

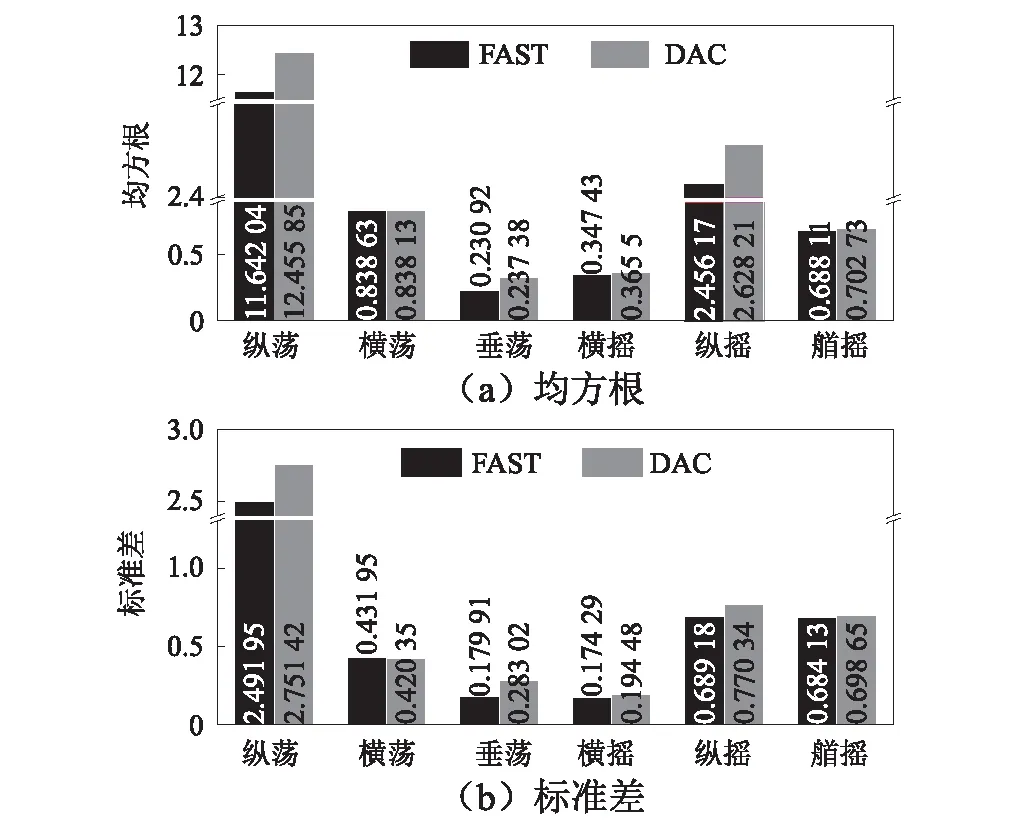
圖10 平臺動態響應的均方根及標準差

由圖10可知，在橫蕩、垂蕩、橫搖及艏搖方向上不同控制策略對其影響較小；縱蕩及縱搖方向上，較之FAST，DAC作用下的均方根分別增大6.99%及7.00%，標準差分別增大10.41%及11.78%。因此，不同控制策略對于海上風力機的影響主要集中在縱蕩及縱搖方向。

4.3 海上風力機漂浮穩定性頻域分析

海上風力機在縱蕩及縱搖方向的漂浮穩定性受不同控制策略影響很大。對縱蕩及縱搖方向的時域曲線進行傅里葉變換，可得如圖11所示的頻域范圍內幅值曲線。

根據圖11可知，對于Spar平臺，在縱蕩及縱搖方向上的固有頻率分別為0.008 Hz及0.032 Hz；較之于DAC，海上風力機縱蕩及縱搖在FAST控制策略下在固有頻率點有著更小幅值，特別是在縱搖方向固有頻率點，無論是縱搖方向還是縱蕩方向，在FAST控制策略下都有著更小的幅值。因此，在海上風力機的變槳控制策略設計時應該首先避免其縱搖方向的固有頻率以提高海上風力機漂浮穩定性。

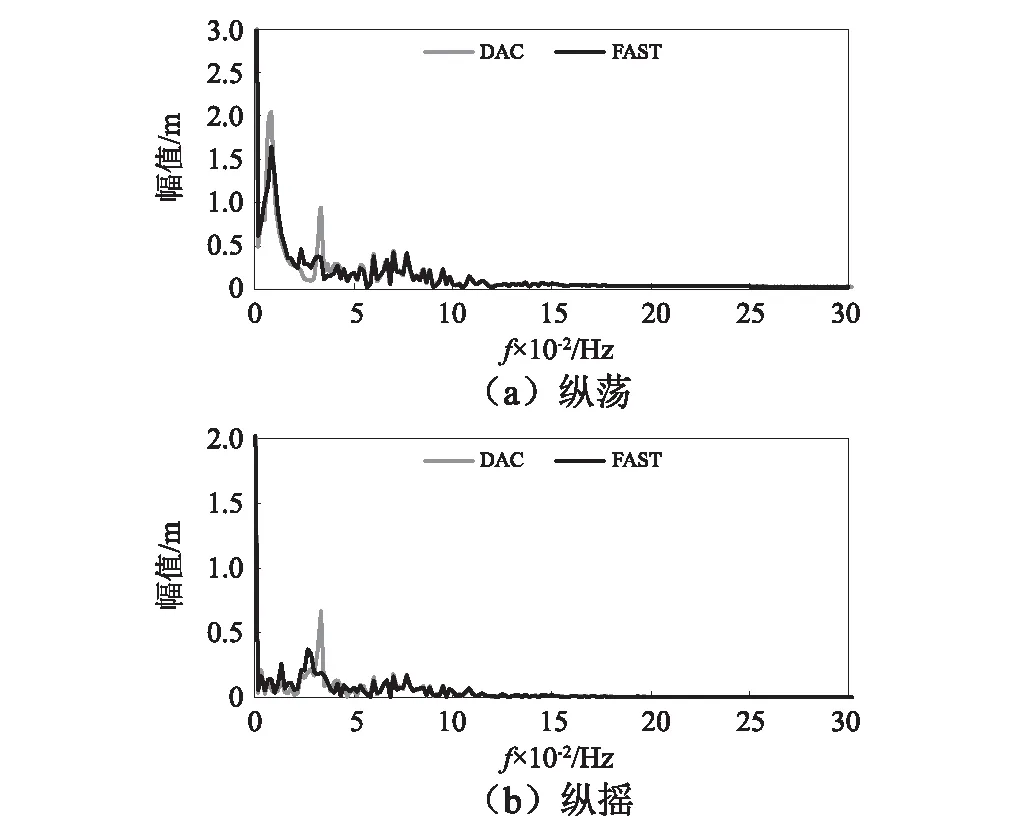
圖11 頻域曲線

5 結 論

基于FAST與Matlab/Simulink聯合仿真平臺，建立DAC控制策略，并與FAST原有的控制策略對比分析不同控制策略對海上風力機控制效果，且研究不同控制策略對基于Spar平臺的海上風力機漂浮穩定性的影響，可得如下結論：

(1)較之于FAST控制策略，海上風力機在DAC控制風輪轉速及輸出功率更穩定，但漂浮穩定性較差。

(2)不同控制策略主要影響海上風力機的縱搖及縱蕩兩個方向的動態響應，對于其他方向的動態響應影響較小。

(3)在縱搖方向固有頻率點，較之于DAC，海上風力機縱搖及縱蕩在FAST控制策略下都有更小的幅值，故在海上風力機的變槳控制策略設計時應該首先避免其縱搖方向的固有頻率以提高海上風力機漂浮穩定性。