二維地基波阻板隔振的復變函數解

周鳳璽， 鄭 琦

(1. 蘭州理工大學 土木工程學院，蘭州 730050； 2. 西部土木工程防災減災教育部工程研究中心，蘭州 730050)

隨著城鎮化建設和現代工業的迅速發展，各種振動問題日益頻繁，環境振動已經成為一種新形式的環境污染，并被列為當前世界的七大環境公害之一。而隨著人們生活水平的提高，對生活環境和工作環境的質量要求也越來越高，對振動的限制越來越嚴格，環境振動及其治理已經成為巖土工程的一個研究熱點問題。

自Woods[1]通過一些現場原位試驗，研究了近場主動隔振和遠場被動隔振的隔振效果，并且提出了一個評判屏障隔振效果的重要參數振幅衰減系數以來，國內外學者對連續屏障和非連續屏障的減振隔振效果進行了一系列的研究工作。比如在振源或需保護結構地基中設置隔振屏障(比如空溝、多排樁、空心管樁等)來降低其振動水平是目前進行地基減振隔振的主要措施[2-5]。由于受表面激振的層狀地基中波的傳播存在截止頻率，當激振頻率低于截止頻率時，地基中不存在波的傳播現象。基于此現象，Schmid等[6]建議使用一個剛性層來形成有限尺寸的人工基巖，并將這個人工基巖稱為波阻板(Wave Impeding Block,WIB)。隨后他們采用二維頻域邊界元法，分析了WIB主動隔振和被動隔振，結果表明WIB的被動隔振效果好于填充溝。采用邊界積分方程法，Peplow等[7]研究了二維雙層地基波阻板主動隔振的隔振效果。利用邊界元和有限元法，Takemiya[8-9]研究了WIB的隔振效果。基于層狀介質中土與結構動力相互作用的半解析邊界元法模型，高廣運等[10-11]分別分析了二維和三維層狀地基中波阻板的隔振效果。隨后，針對三維豎向非均勻和飽和地基模型，高廣運等[12-13]對軌道交通荷載作用下豎向非均勻地基和飽和地基中波阻板的隔振性能進行了研究。李寧等[14]通過現場試驗，先研究了水平激振下混凝土材料的WIB對層狀地基的隔振效果，又分析了WIB的埋深對隔振效果的影響，并對比了實測的位移結果與半解析邊界元方法計算的結果。基于Biot多孔介質波動理論，結合PML邊界條件，高貝貝[15]用時域有限元方法研究了二維地基中儲液多孔波阻板的隔振性能。基于Biot多孔介質波動理論和功能梯度材料，周鳳璽等[16-17]研究了含液飽和多孔波阻板和梯度波阻板的地基振動控制研究，結果表明含液飽和多孔波阻板和梯度波阻板的地基隔振體系更加具有優越性。利用傅里葉級數展開的方法，引入輔助函數和波函數展開技術，張海等[18]研究了彈性半空間中含直邊界半圓形襯砌隧道對SH波的散射解析解。結合Green函數法及裂紋“切割”技術，采用保角映射的方法，楊在林等[19]研究了SH波下方入射時半無限空間界面附近橢圓形彈性夾雜及任意位置直線裂紋對SH波的散射問題。

由于WIB隔振設計屬于土與結構動力相互作用問題，由于其復雜性目前常用的分析方法主要是數值模擬(邊界元法、有限元法)和試驗驗證。但是，對于WIB隔振性能的解析分析較少。因此，本文借助復變函數的積分變換法將有限長度的波阻板變換為單位圓，建立了二維彈性地基中矩形波阻板對波場散射問題的控制方程。考慮平面SH波入射，運用波函數展開法得到了二維地基波阻板隔振性能的解析解答。通過數值算例，分析了波阻板剪切模量、波阻板埋深、彈性波入射角度對隔振效果的影響。

1 WIB的保角映射變換

根據復變函數理論，通過映射函數z=ω(η)可將波阻板所在z平面上所占的區域變換為復平面η上的單位圓，保角映射前后的坐標系統如圖1所示，其中H表示WIB埋置深度，α表示SH波入射角度，相應的保角映射公式為[20]。

(1)

式中：

c1=cos(2χπ)

(2a)

(2b)

(2c)

(2d)

式中：χ為取決于WIB長寬比a/b的系數；系數c1∶c7僅與χ有關；R為與WIB尺寸有關的實數，可由以下兩式中的任意一式計算：

(3a)

(3b)

對于正方形，即長寬比a/b取1時，χ=0.25；而其他矩形，可采用試算法求χ，即估計一個χ值，由式(2)求得c1∶c7，代入式(1)可得映射函數，它是一個微曲的矩形。以寬度0.4 m，長度4.0 m的WIB為例，經試算得到χ=0.106 5，圖2給出映射波阻板以及與單位圓的對應關系，將矩形波阻板所在z平面上所占的區域變換為復平面η上的單位圓。

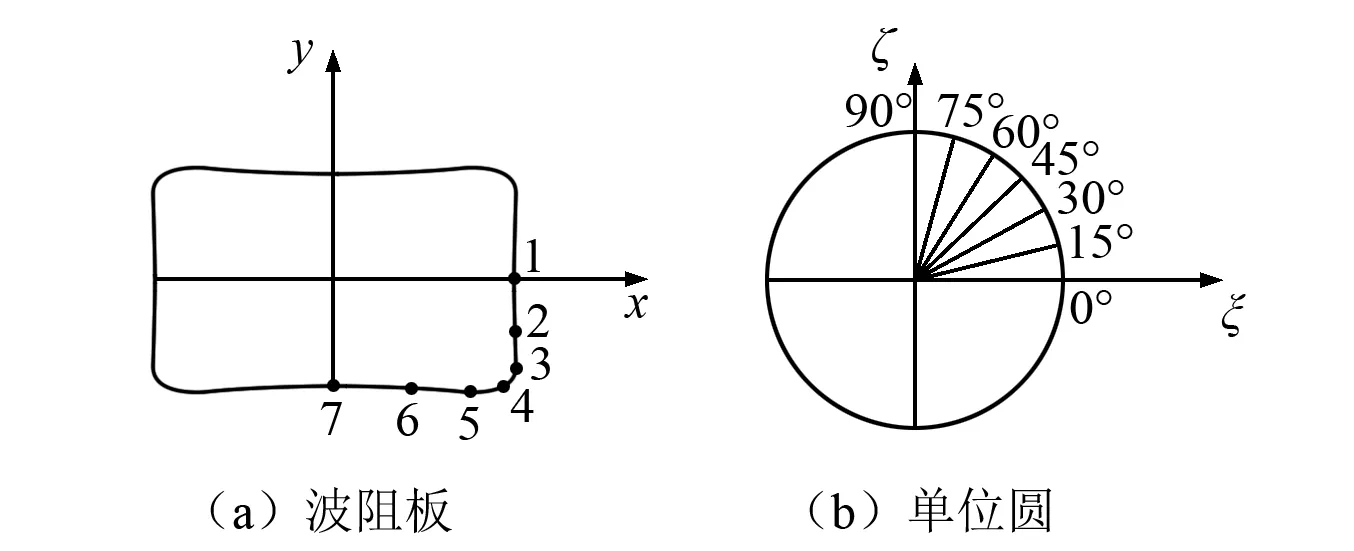
圖2 映射波阻板與單位圓的對應關系

2 控制方程

穩態平面SH波入射含WIB的二維彈性地基中，引起了散射波位移場為垂直xy平面的位移分量w(x,y)(省略了時間因子e-iωt)，且應滿足Helmholtz方程：

(4)

應力和位移的關系為：

(5a)

(5b)

(6)

(7a)

(7b)

而在復坐標系中，應力表達式為：

(8a)

(8b)

式中：θ為曲線坐標系(r,θ,z)中r軸與直角坐標系中x軸之間的夾角。

3 WIB對SH波的散射

3.1 入射波場

(9a)

(9b)

式中：w0為入射波的波幅；α為入射角；kS為波數。

由(7)可知w(i)和w(r)相對應的應力場為：

(10a)

(10b)

(10c)

(10d)

3.2 散射波場

(11)

由式(7)可得到散射波對應的散射應力場為：

(12a)

(12b)

同理，WIB結構內的散射波為：

(13)

所對應的應力場為：

Jn+1(kB|z|)(z/|z|)n+1e-iθ

(14a)

Jn+1(KB|z|)(z/|z|)n+1e-iθ}

(14b)

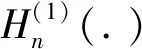
3.3 邊界條件

(15a)

(15b)

3.4 問題的解答

將式(9)，式(11)和(13)代入式(15a)，整理后可得

(16a)

將式(10)，式(12)和式(14)代入式(15b)，可得

(16b)

用e-imθ乘方程(16)的兩邊，并在區間(-π,π)上積分，則得到關于待定復系數An和Bn的理論解的無窮線性方程組：

(17)

其中：

利用截斷有限項的方法解出方程組(17)。就可以確定波函數中未知系數An和Bn，并將未知系數An和Bn代入式(9)、(11)、(13)，即求得彈性半空間介質的位移場和WIB的位移場。

4 分析討論

為驗證本文解答的正確性，選取王貽蓀[22]對Lamb問題的解析解答。利用突加力問題的閉合解求得了Lamb問題的解答，避免了對難以積分形式解的求積。取彈性地基密度ρs=2×103kg/m3，剪切波速為cs=200 m/s，固有圓頻率為ω=10 Hz，剪切模量為μS=80 MPa。對比結果見圖3。由圖3看出，本文計算值與文獻[22]結果相一致，說明本文的算法有效。

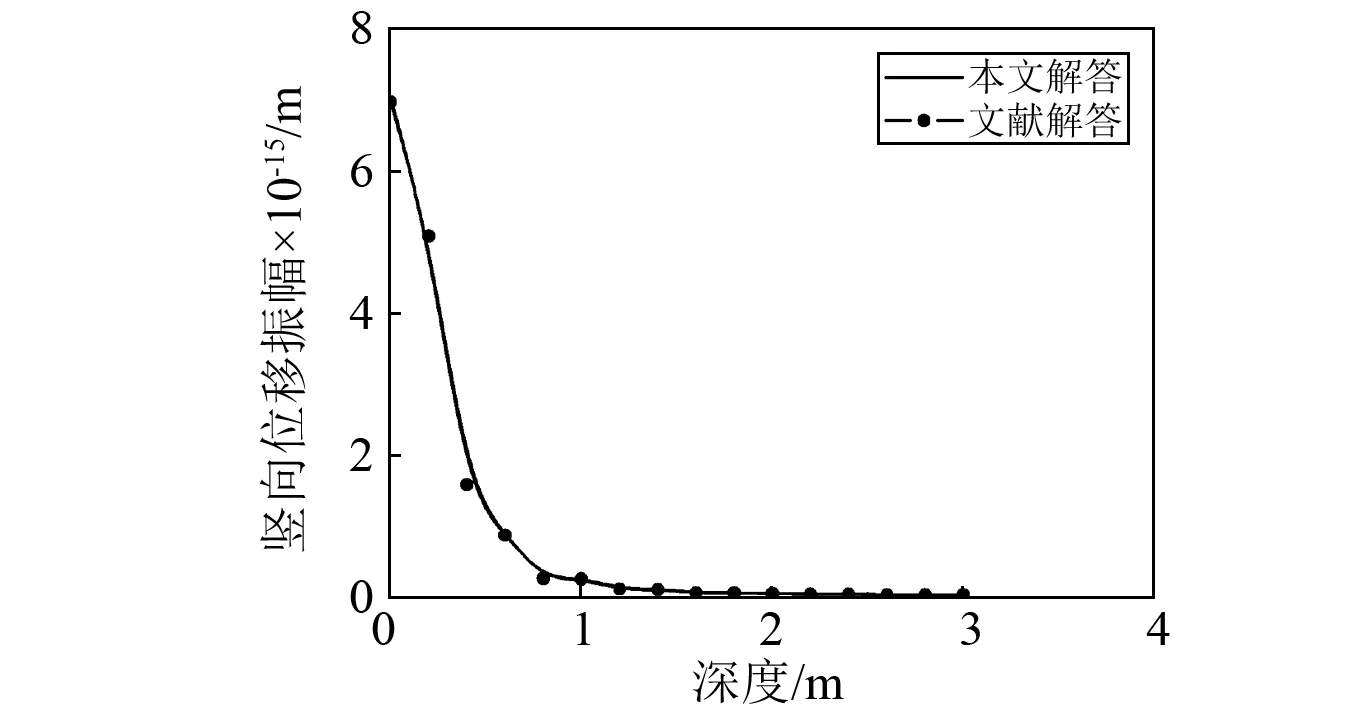
圖3 SH荷載激振地表振幅解答對比

對于WIB隔振效果的評價，Woods提出用振幅衰減系數AR來衡量[1]：

AR=有屏障時振幅/無屏障時振幅

且AR≤0.25時隔振效果較好。

為了分析級數項系數對數值計算結果的影響。選取參數a=4 m，b=0.4 m，ρS=2×103kg/m3，ω=10 Hz，μS=80 MPa，kS=0.05，kS/kB=1/3，μB/μS=2，H=0.5b，α=30°。圖4給出了不同n的情況下地表豎向位移振幅的變化曲線。由圖4知，當散射波系數n取10時可以滿足計算精度要求。

分析剪切模量比對隔振效果的影響，選取a=4 m，b=0.4 m，ρS=2×103kg/m3，ω=10 Hz，μS=80 MPa，kS=0.05，kS/kB=1/3，H=0.5b，α=30°。圖5繪出了地表振幅衰減系數的變化曲線。由圖5知，當WIB的剪切模量與地基的剪切模量比為μB/μS=0.5時，采用WIB隔振體系隔振效果不是很明顯，當剪切模量比為μB/μS=1時，可以看出WIB有顯著的隔振效果；當μB/μS=2時，隔振效果顯著增強。所以，應根據隔振設計實踐的需求，合理地選擇WIB的剪切模量可以有效提高隔振效果。

圖4 豎向位移振幅的變化曲線

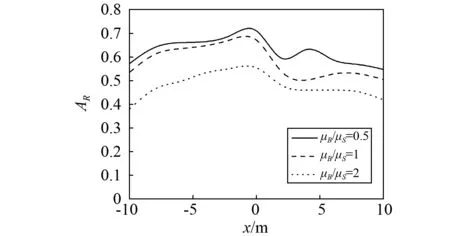
圖5 不同WIB剪切模量時振幅衰減系數AR變化曲線

其余參數不變，取模量比μB/μS=2時，圖6給出了WIB的埋深對地表振幅衰減系數的變化曲線。從圖6可以發現，隨著埋深的增大對地表振幅的隔振效果減小。

圖6 不同WIB埋深時振幅衰減系數AR變化曲線

為了討論了不同的入射角度變化對地表幅值的影響。圖7給出了kS/kB=1/3，H=0.5b時地表振幅衰減系數的變化曲線。由圖7知，地震波入射角度α對隔振效果有著明顯的影響，隨著入射角度的增大隔振效果明顯減小，當α=90°時，隔振效果減小尤為明顯。

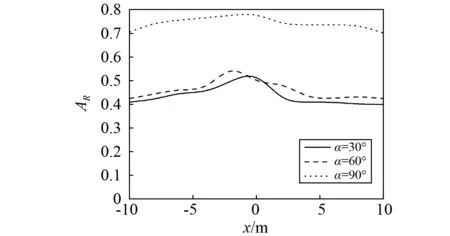
圖7 不同入射角度時振幅衰減系數AR變化曲線

5 結 論

運用復變函數的保角映射方法和波場勢函數展開法，得到二維彈性地基WIB隔振的解析解答，通過參數分析討論了WIB剪切模量、埋深、彈性波入射角度對隔振效果的影響，研究表明：隨著WIB剪切模量的增大其隔振效果明顯增加，隨著WIB埋置深度增加隔振效果逐漸減小，并且WIB的隔振效果隨彈性波入射角度的增大而減小。