超共振振動轉子系統振動同步及同步傳動

陳 幫， 夏曉鷗， 王曉波

(1.北京科技大學 機械工程學院, 北京 100083；2.北京礦冶科技集團有限公司, 北京 100160)

自同步技術及相關設備已廣泛應用于工業生產中[1-3]。振動自同步研究內容涉及非線性振動、機電耦合、自動控制理論等[4-8]。轉子安裝在可振動體上形成振動轉子系統，兩個振動轉子系統的振動機體通過彈簧連接形成雙振動轉子系統，如圖1所示。控制連接彈簧的剛度以及機體的運動軌跡，可轉化為多種動力學系統，例如將連接彈簧趨于無限大，即為雙轉子固定于同一機體上的振動系統；將某一機體的運動軌跡設計為圓弧，即為擺動系統。討論兩個振動轉子系統之間的耦合行為，對振動同步研究具有積極的學術意義。

近年來，Peňa、Jovanovic、Dilao等[5-10]學者分析了不同參數對擺同步行為的影響，包括擺的同向及反向同步。Czolczynski利用節拍器研究兩個及多個擺之間的耦合同步現象，討論了系統的能量傳遞情況。Koluda等[11-12]研究了耦合擺之間的自同步行為。擺動同步理論不斷豐富[13-15]，顯示了擺動同步的多樣性。Blekhman等[16-17]首次研究了轉子自同步現象，得出了安裝在同一機體上轉子自同步的條件。Wen等[18]發展了振動自同步的研究，研究成果應用于工業生產，取得了良好效果。Zhao等[19-21]采用改進小參數法研究振動自同步，討論了多種類型振動系統的轉子同步行為。劉勁濤等[22]研究了反共振機械的振動同步問題。李凌軒等[23]研究了雙機振動系統分別在亞共振與遠共振條件下的同步性問題。Zhang等[24-27]分別研究了三轉子振動系統的同步行為。同時，侯勇俊設計了雙轉子橢圓振動機，Fang[28]分析了該系統的轉子耦合擺動力學行為。

上述研究多側重于安裝在同一振動體上的擺或轉子同步研究，對于振動轉子系統的耦合同步研究較少。作為高頻雙動顎振動破碎機的理論模型，超共振雙振動轉子系統的同步特性隨耦合彈簧剛度的變化情況尚不明確。針對該問題，本文擬利用動力學方法研究系統的振動情況，闡明系統的振動同步與振動同步傳動特性；以振動力矩為切入點，深入討論耦合彈簧對系統同步的影響，揭示該系統實現高穩定性與高容差性的耦合機理，為開發高可靠性振動設備和激振系統提供參考。

1 雙振動轉子系統

如圖1所示，轉子1和轉子2分別安裝在振動體1和振動體2上。彈簧kp兩端分別固定在兩個振動體上，阻尼記為fp。m1，m2分別表示轉子質量，φ1，φ2分別表示轉子連桿與水平方向的夾角。轉子對應的驅動力分別為Te1，Te2，阻力分別為Tf1，Tf2，阻尼系數分別為fr1，fr2。令轉子逆時針方向轉動為正。振動體可在水平方向上運動，質量為M1，M2，位移分別表示為x1，x2，與地基連接彈簧剛度與阻尼分別為k1、f1、k2、f2。轉子關于質心的轉動慣量分別為j1，j2，偏心距分別為r1，r2。

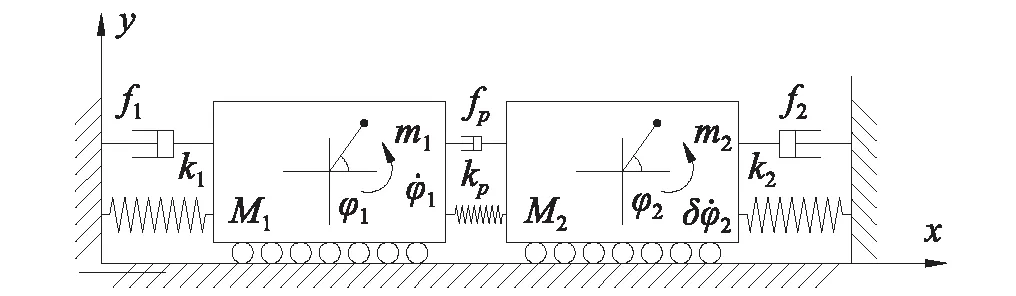
圖1 雙振動轉子振動模型

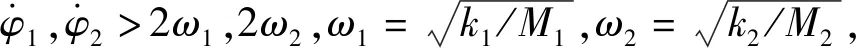
其中：

勢能與耗散函數分別為

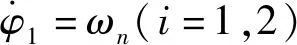
式中：ni，Lmi，ωsi，Lsi，Rri分別對應電機的極數、互感系數、同步轉速、定子電感、轉子電阻；U0為電機電網的電壓幅值。建立系統的振動微分方程如下

(1)

2 同步研究

由式(1)可知，所研究模型是剛度耦合的振動系統。由轉子自同步的相關定義可知，轉子實現振動自同步時，系統穩定運動，速度波動較小。為簡化計算并考慮實際工業應用，系統的彈簧阻尼均很小，彈簧k1與彈簧k2的阻尼相同。根據學者Blekhman的研究，忽略小變量。在一階近似條件下簡化式(1)得

(2)

其中

(3)

系統同步轉速為ωn，記轉子的相位如下

φ1=ωnt+α,φ2=ωnt+α2

(4)

如上節說明系統運行遠離共振區，α1，α2為慢變函數。由式(2)～(4)得

x1=a11cos(φ1+γ11)+a12cos(φ2+γ12),x2=a21cos(φ1+γ21)+a22cos(φ1+γ22)

(5)

式中

(6)

a11,a12,a21,a22體現了振動體之間、轉子之間、轉子與振動體之間的耦合作用。顯然，a12，a21越大，振動轉子之間的耦合作用越強。根據轉速與振動固有頻率關系，可分為前共振(ωn<ω1,ω2)與超共振雙振動轉子系統(ωn>ω1,ω2)。考慮超共振雙振動轉子同步行為特性及其工業應用的特點，本文重點研究超共振雙振動轉子系統。

γ11,γ12,γ21,γ22是由于阻尼作用相應產生的相位滯后。由于研究模型為弱阻尼系統，相位滯后可計算為γ11=f1a11/(m1r1ωn)、r12=f1a12/(δm2r2ωn)、γ21=f2a21/(m1r1ωn)、γ22=f2a22/(δm2r2ωn)，其中γ12=γ21。

3 轉子的同步性及其穩定性

利用平均法將快變運動(高頻)與慢變運動(低頻)分開討論，是分析非線性振動問題的一種實用手段。定義運算，若h(t)是周期函數，其在一個周期T上的平均值記為〈h(t)〉，如下式

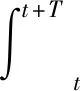
(7)

轉子同步運轉時，轉子所受的加速度平均值為0，或者合力矩在一個周期上平均值為0，因此

(8)

轉子依靠電機驅動，電機的阻力近似與轉速成正比。轉子穩定旋轉時，轉速波動較小，由趙春雨，張學良以及方潘的研究可知，感應異步電機輸出力矩的動態特性可線性化。因此在穩定轉速附近，可用Tei(ω)，Tfi(ωn)代替〈Tei(ω)〉，〈Tfi(ω)〉進行討論。系統同步穩定運行時，定義轉子受到合力矩的平均值為P1，P2，則

(9)

(10)

由式(5)、(6)、(9)以及(10)得

(11)

令：

(12)

系統為弱阻尼系統，γ11、γ22為小參數，則式(9)，(10)可簡化為

(13)

(14)

Tv為系統的振動力矩，作用在轉子上調節轉子之間的能量分配，是系統實現振動自同步的關鍵指標，其大小與轉子的同步轉速、振動體質量、支撐彈簧、耦合彈簧等參數有關。式(13)，(14)相減得

P1-P2=Te1(ωn)-Te2(ωn)-
[Tf1(ωn)-Tf2(ωn)]-Tv

(15)

定義

Δα=α1-α2-γ12,
ΔTe(ωn)=Te1(ωn)-Te2(ωn),
ΔTf(ωn)=Tf1(ωn)-Tf2(ωn)

(16)

由式(6)，(8)以及(15)得

(17)

定義系統同步指數D為

(18)

所以

(19)

若關于方程式(17)有實數解，要求式(17)右邊的絕對值小于或等于1，所以系統實現自同步的條件為

|D|≥1

(20)

分析式(13)～(15)可知，振動力矩Tv是系統能否實現自同步的關鍵因素，其大小與耦合系數a12，a21相關，其值越大，系統越易實現自同步。可通過Lyapunov穩定性理論討論系統同步的穩定性。雙振動轉子系統中有

P1-P2=ΔTe(ωn)-ΔTf(ωn)-Tv

(21)

系統可維持自同步運行狀態的穩定性條件為

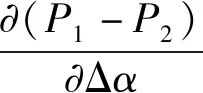
(22)

結合式(6)，(12)得：

(23)

式(23)即是轉子自同步運行的穩定性條件。其穩定運行的狀態與轉子的轉向相關，轉子同向旋轉與反向旋轉的穩定運行相位差處于不同象限。

由上述討論可知，系統穩定同步運行時，振動力矩可以作為驅動力作用在轉子上，若該驅動力矩足夠大，能夠克服轉子受到的阻力矩，則可關閉該轉子的電機，在振動力矩的作用下轉子依然保持同步轉動，即實現振動同步傳動。若在系統穩定運行后，只開啟轉子i(i=1,2)的驅動電機，系統可保持振動同步轉動，對應同步指數為DTi，式(18)變為

(24)

系統穩定運行后，只開啟轉子i的驅動電機，系統能夠實現振動同步傳動的條件為

|DTi|≥1

(25)

電機的開啟或關閉并沒有體現在穩定性條件式(23)中，因此穩定性條件仍為式(23)。

4 模型討論

雙轉子振動系統是兩個振動系統間的耦合動力學模型。在一定條件下，系統滿足自同步條件，即使電機、轉子質量、偏心慣量、振動體質量等振動參數有明顯差異，仍可實現同步旋轉。根據公式(6)、(20)、(23)以及(24)，控制連接彈簧的剛度，可直接增強或降低系統之間的耦合作用，使系統在不同狀態下同步運轉，并具有一定的穩定性。本文討論模型的相關研究數據，如表1所示。

表1 系統動力學參數

振動體之間通過彈簧連接，不同于兩個振動體固定在一起，特點是通過彈簧代替剛體連接，由系統的同步方程式，可直觀認為，在不改變其他參數的情況下，可通過連接彈簧控制振動力矩的大小。自同步現象是振動力矩與轉子輸入轉矩之差共同作用的結果。顯然的，耦合彈簧kp的大小會影響系統之間耦合作用，表現出對振動力矩傳遞效率的影響。分析式(6)與(12)，有如下關系式：

(26)

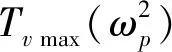
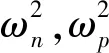
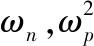
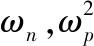
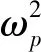
(27)

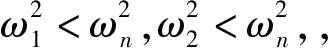
(28)

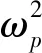
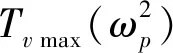
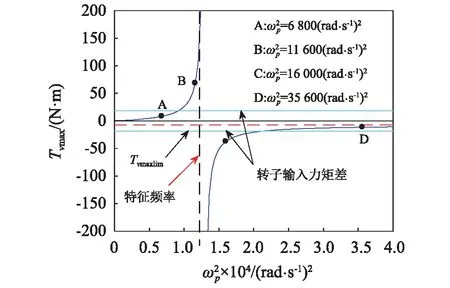
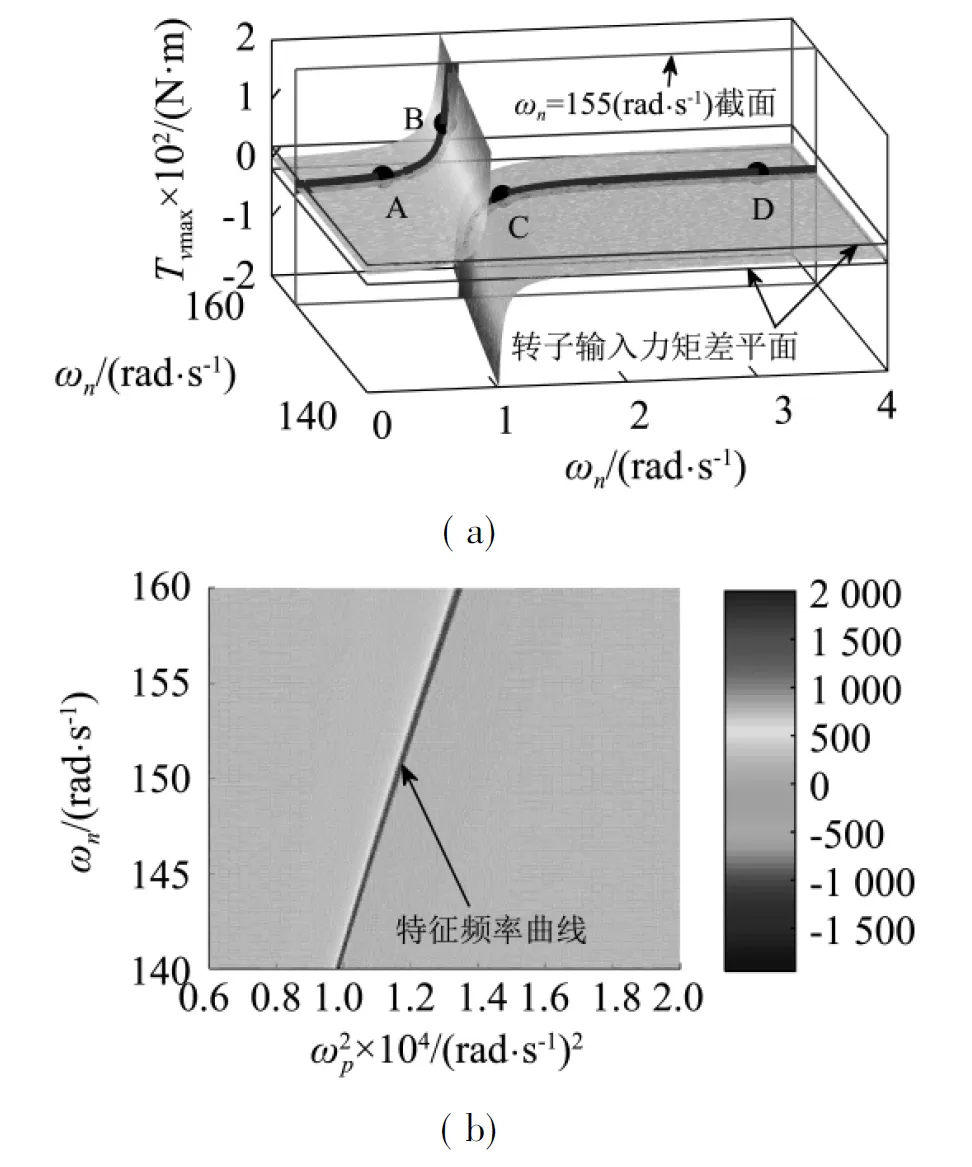
圖3 ωn=155 rad/s時最大振動力矩關于耦合頻率的關系

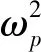
圖3中曲線Tv max的兩個部分被轉子的輸入力矩差±(ΔTe(ωn)-ΔTf(ωn))曲線分割為4個部分，分別定義為LineA(包含點A)、LineB(包含點B)、LineC(包含點C)、LineD(包含點D)。根據式(19)，(20)可知，處在兩條輸入力矩差之間的部分(即|Tv max|<|ΔTe(ωn)-ΔTf(ωn)|)，無論同步相位差如何變化，系統無法實現自同步，因此系統在LineA與LineD上時，無法實現振動自同步；處在兩條輸入力矩差之外的部分(即|Tv max|>|ΔTe(ωn)-ΔTf(ωn)|)，在穩定運行時，可滿足同步條件，因此曲線在LineB與LineC上時，系統能夠實現振動自同步。

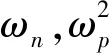
當ωp→+∞，即kp→+∞，則：

(29)

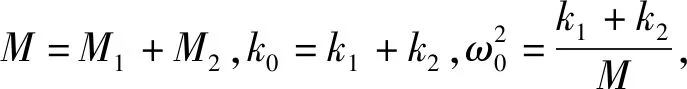
(30)

式(19)為

(31)

相應的轉子實現自同步的穩定性條件根據式(22)可得：

(32)

由于最大振動力矩關于耦合頻率的變化，在特征頻率右部是連續單調遞增的，因此可以認為，在兩個振動體相互固定時，其最大振動力矩達到極限Tv max lim。

圖2，圖3以及上述分析表明，系統耦合頻率在特征頻率附近時，或系統參數狀態在特征曲線附近時，系統耦合性能強，易實現振動自同步。調節連接耦合彈簧的大小，可改變最大振動力矩的大小，從而控制系統的同步性能與同步狀態。安裝于同一振動體上的雙轉子振動系統同步行為，可以認為是雙振動轉子系統中連接彈簧趨于無限大的一種特殊情況。在超共振系統中，兩個轉子之間通過剛體連接(兩個轉子安裝在同一機體上)的耦合性能并不是最大。該結論的意義在于，在單質體或雙質體雙轉子同步振動系統中，當兩個轉子難以實現振動自同步時，可設計將原本安裝在同一機體上兩個轉子，安裝在具有一定剛度的柔性體上，或者分別安裝在兩個通過彈簧連接的機體上，控制耦合頻率，可以增強系統的耦合作用。此時系統可獲得更為寬松的振動同步條件，穩定性與容差度可進一步提升。

5 同步性數值仿真

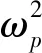
(a)

(b)

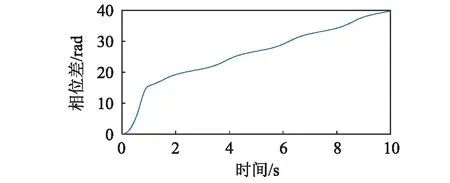
圖4顯示了連接彈簧剛度kp為1.36×106N/m時，轉子的運動狀況。分析圖2，圖3及式(19)可知，該狀態下，轉子輸入力矩之差的絕對值|ΔTe(ωn)-ΔTf(ωn)|大于振動耦合所產生的最大振動力矩|Tv max|的絕對值，式(19)無實數解，不存在振動自同步狀態。由圖4(a)可知，轉子1與轉子2的轉速在穩定運轉時不相同，圖4(b)顯示轉子的相位差逐漸增大。

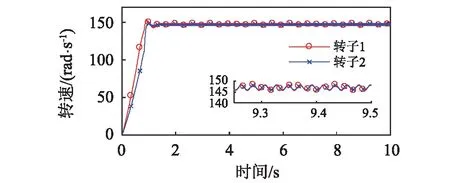
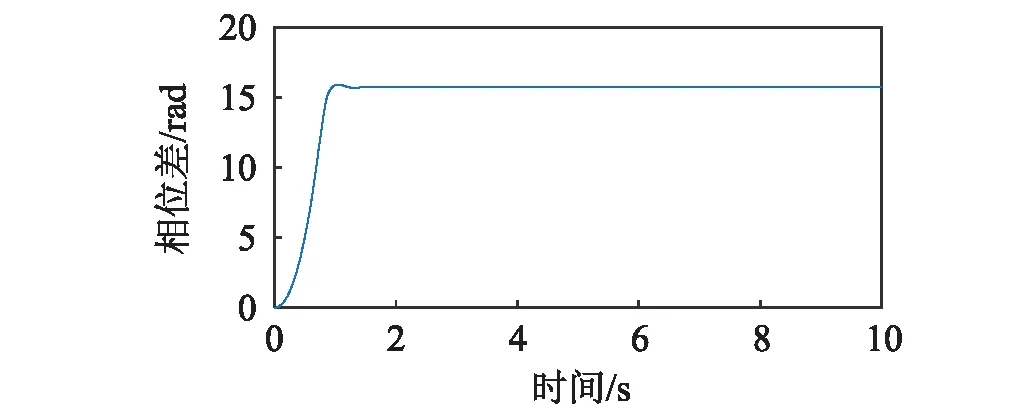
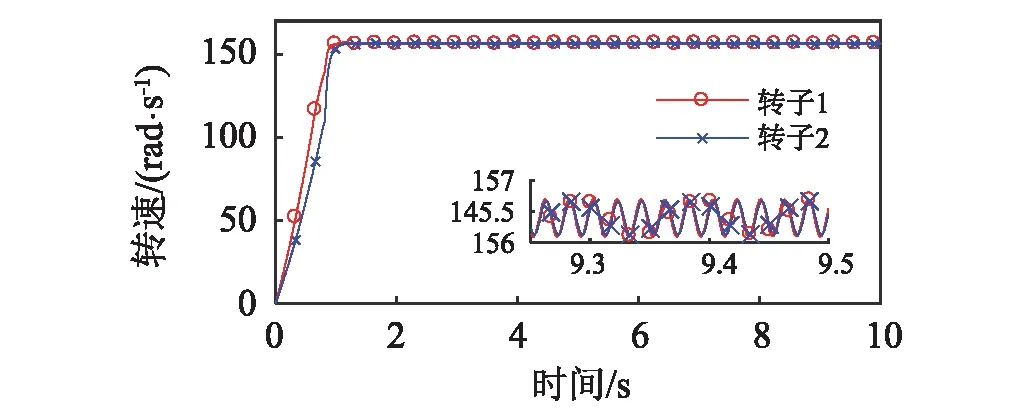
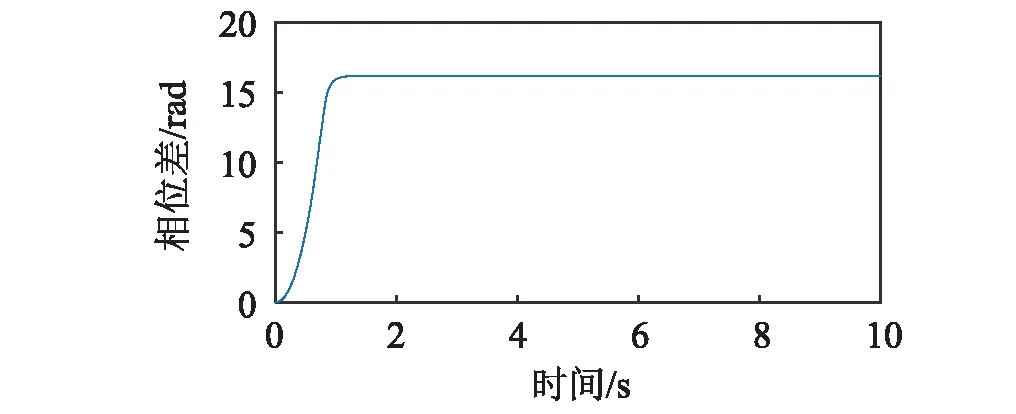
圖5顯示了連接彈簧剛度kp為2.32×106N/m時，系統的振動情況。分析圖2，圖3及式(19)可知，該狀態下，轉子輸入力矩之差的絕對值|ΔTe(ωn)-ΔTf(ωn)|小于振動耦合所產生的最大振動力矩|Tv max|的絕對值，滿足系統的振動自同步條件。由式(17)及式(23)計算相位差得Δα=3.28 rad。圖5(a)表明轉子1與轉子2的轉速在系統穩定運轉時趨于相同，在1.4 s左右實現振動同步；圖5(b)顯示轉子的相位差穩定在15.83 rad(15.81-4×π=3.26 rad)。數值分析與理論分析基本一致。圖6顯示了連接彈簧剛度kp為3.2×106N/m時，轉子的運動狀況。同樣的，該狀態滿足系統振動自同步條件。理論計算得Δα=3.65 rad。由圖6(a)可知，轉子1與轉子2的轉速在1.4 s左右實現振動同步；圖6(b)顯示轉子的相位差穩定在16.20 rad(16.20-4×π=3.63 rad)。數值分析與理論分析基本一致。

(a)

(b)

(a)

(b)

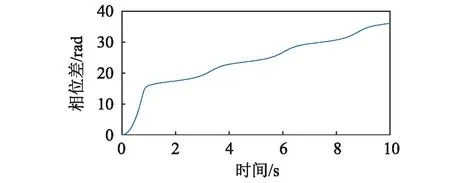
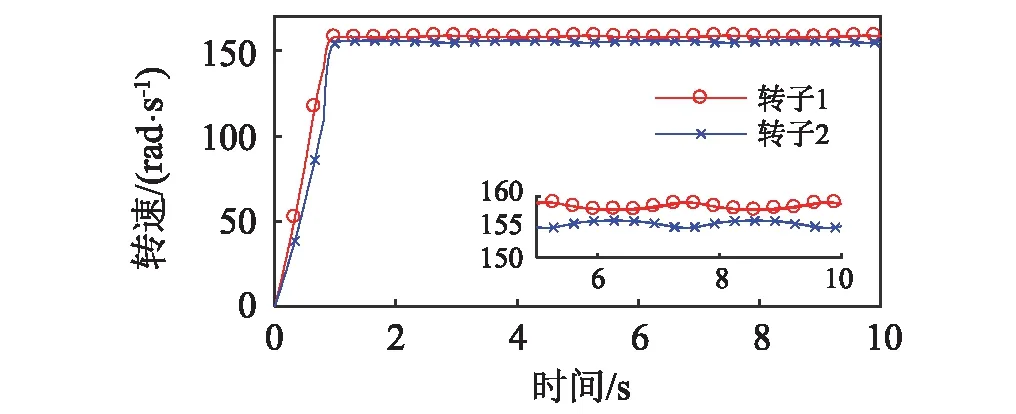
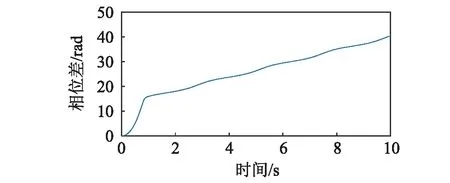
連接彈簧剛度kp為7.12×106N/m時，轉子的運動狀況如圖7所示。由圖2，圖3及式(19)可知，此時系統不滿足系統的振動自同步條件。圖7(a)顯示了轉子1與轉子2的轉速在穩定運轉時不統一，圖7(b)顯示轉子的相位差逐漸增大。連接彈簧剛度趨于無窮大時，轉子的運動狀況如圖8所示。同樣，該狀態不滿足系統的同步條件。由圖8(a)可知，轉子1與轉子2的轉速在穩定運轉時不同步，圖8(b)顯示轉子的相位差逐漸增大。

(b)

(a)

(b)

6 振動同步傳動數值仿真

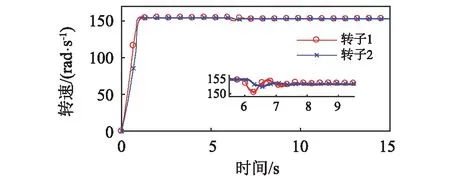
(a)

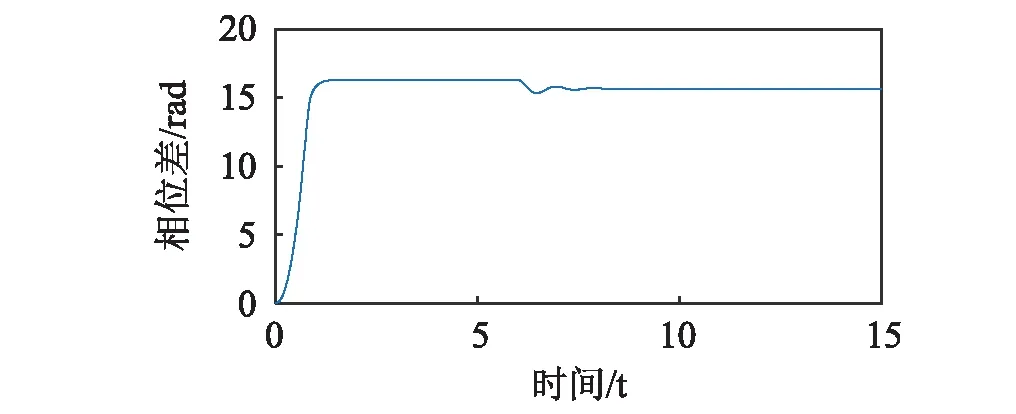
(b)

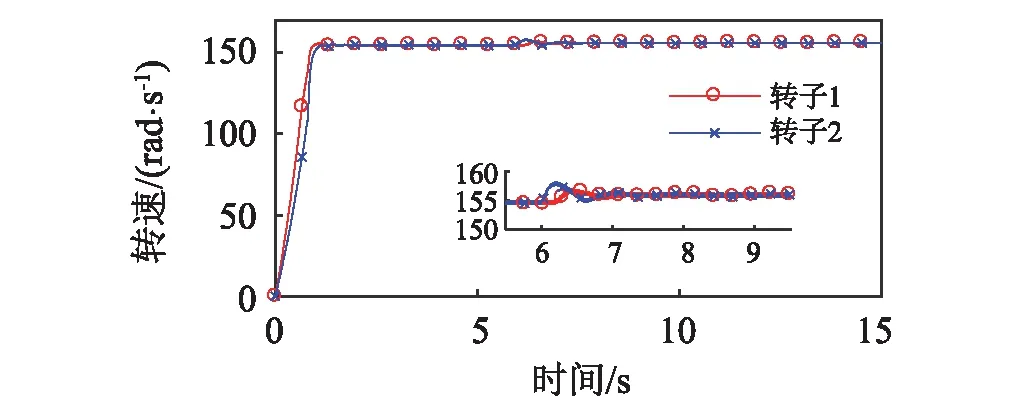
(a)

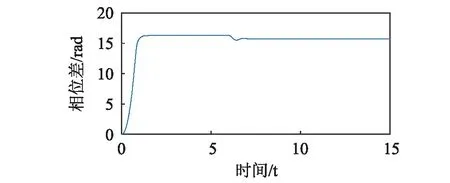
(b)

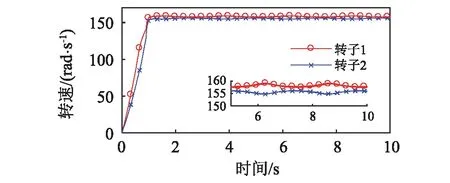
圖9顯示兩個轉子在開機后2 s附近時實現振動自同步，轉速一致為ωn=154.67 rad/s。在6 s時，去除轉子1的驅動，經過耦合作用，轉子1與轉子2仍可保持同步運轉，轉速較之前略有降低，相位差回落；此時ωn=153.15 rad/s，Tv max=-29.17 N，ΔTe(ωn)-ΔTf(ωn)=0.6162 N，滿足式(25)的同步條件。圖10顯示了系統轉子實現自同步運轉后，在6 s時，去除轉子2的驅動，經過耦合作用，轉子1與轉子2同樣可保持同步運轉，轉速較之前卻有增加，相位差相應發生變化；此時ωn=155.99 rad/s，Tv max=-34.85 N，ΔTe(ωn)-ΔTf(ωn)=1.41 N，滿足式(25)的同步條件。系統轉子實現自同步運轉時，振動力矩Tv平衡兩個轉子的能量輸入差ΔTe(ωn)-ΔTf(ωn)，作用在落后的轉子上為驅動力矩，作用在超前的轉子上為阻力矩。在特定條件下，超前轉子的驅動電機不僅輸出能量維持系統的振動，還輸出能量至落后轉子的驅動電機。此時，落后轉子的驅動電機實際上吸收能量。若兩個轉子可實現振動同步傳動，將落后轉子的電機從系統中去除，則該電機不會從系統中吸收能量，系統因此會獲得較多能量，同步轉速反而提高；若將超前轉子的電機從系統中去除，則落后電機需向系統中輸出能量維持系統振動，輸出力矩為正，轉速因而降低，相位差發生變化。若系統的阻尼較大，兩個轉子的輸出力矩均為正，則在振動同步傳動時，同步轉速均會降低。

7 結 論

(1)超共振雙振動轉子系統是一種具有自同步特性的振動系統，控制系統參數可轉化為不同類型振動系統。在一定條件下，超共振雙振動轉子系統具備良好的自同步性能，具備高穩定性、高容差度的特點。耦合頻率ωp在特征頻率附近時，或系統參數狀態在特征曲線附近時，系統所產生的振動力矩大，轉子易實現振動自同步。雙轉子固定于同一機體的振動系統，可認為是系統連接彈簧趨近無窮大時的一種特定情況。

(2)通過調節連接耦合彈簧kp的大小，可控制系統的同步性能。超共振雙振動轉子系統不僅可以實現轉子的振動自同步，也可實現振動同步傳動。若系統參數滿足相關條件，在轉子實現振動自同步后，切斷一個電機的電源，系統仍可實現振動自同步。

(3)對比B、C點以及ωp→+∞，可知在超共振系統中，兩個轉子之間通過剛體連接(兩個轉子安裝在同一機體上)的耦合性能并不是最大。該結論的工程意義在于，安裝在一個機體上的雙轉子振動系統，若兩個轉子難以實現振動自同步，可考慮兩個轉子安裝在柔性體上，或者兩個通過彈簧連接的機體上，調節兩個振動體支撐彈簧與耦合彈簧的剛度大小，使系統具有更為寬松的振動同步條件。利用該原理設計振動系統可具有良好的穩定性與容差度。