Cahn-Hilliard方程的動態(tài)分歧

武瑞麗,柴容倩,錢小瑞

(四川大學(xué)錦城學(xué)院,四川 成都 611731)

1 引言

分歧問題是自然界中普遍存在的問題,它廣泛存在于物理,化學(xué)和生物等學(xué)科中,分為定態(tài)分歧和動態(tài)分歧.近年來,在研究非線性演化方程的穩(wěn)定性與分歧方面,馬天和汪守宏創(chuàng)立了一套新的分歧理論與躍遷理論[1-2],本文就利用該理論討論了Cahn-Hilliard方程的動態(tài)分歧.

本文考慮如下Cahn-Hilliard方程的初邊值問題:

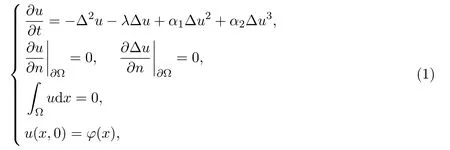
其中λ為參數(shù),α1,α2>0為常數(shù),?=[0,L]×[0,L],n為?邊界處的法向量.Cahn-Hilliard方程被 Cahn和 Hilliard在文獻 [3]中首先引入,用來描述包含兩種物質(zhì)的混合物 (比如合金,玻璃,聚合物等)在達到一種不穩(wěn)定狀態(tài)時所發(fā)生的相分離.近年來對Cahn-Hilliard方程的分歧研究有很多,如文獻[4-5]研究了非自治反應(yīng)擴散方程的拉回吸引子的存在性,文獻[6]考慮了粘性Cahn-Hilliard方程的拉回D-吸引子存在性問題,文獻 [7]研究了具有一般非線性項的Cahn-Hilliard方程的整體吸引子存在性,文獻[8]重點分析了一類帶Neumann邊界條件的Cahn-Hilliard方程的定態(tài)分歧.本文繼續(xù)了文獻[8]的研究工作,運用文獻 [1-2]中提出的分歧理論與躍遷理論對Cahn-Hilliard方程做了進一步的分析,討論了Cahn-Hilliard方程的動態(tài)分歧結(jié)果,給出了其發(fā)生動態(tài)分歧的條件及臨界點,并同時得到了在Neumann邊界條件下,方程分歧出的穩(wěn)定奇點吸引子和鞍點的表達式.

2 預(yù)備知識

在這一部分,首先將Cahn-Hilliard方程進行算子化處理,并詳細計算出其特征值與特征向量,最后給出本文的主要工具―非線性方程的動態(tài)分歧理論[1-2].

2.1 方程的處理

建立空間如下:

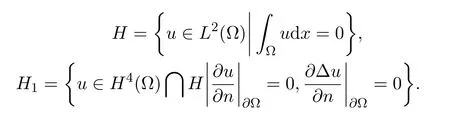
定義如下算子:

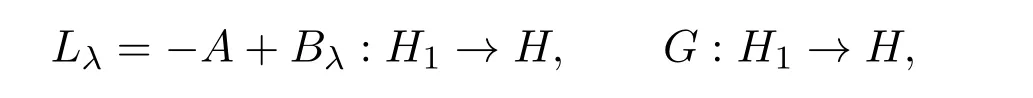
其中

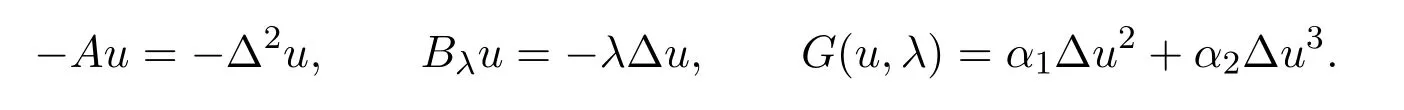
則不難驗證Lλ:H1→H是線性全連續(xù)場,方程(1)可轉(zhuǎn)化為如下抽象形式

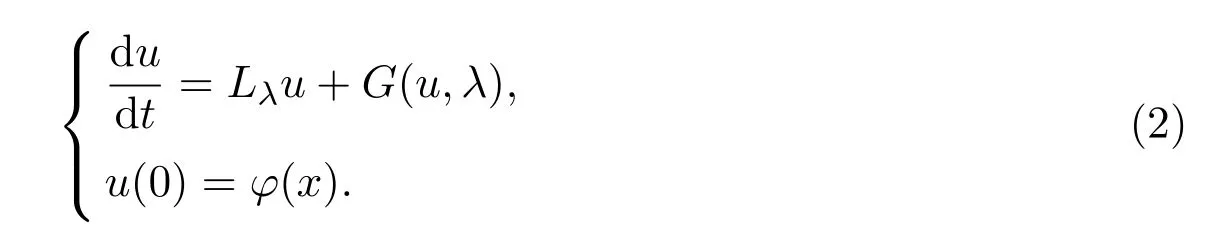
其中,Gλ滿足Gλ:X1→X是一個連續(xù)算子,且Gλ(u)=o(|u|),這樣方程就滿足了線性全連續(xù)場譜理論的條件,因此可以運用該理論.

2.2 算子的特征值與特征向量

令ρk,ψk是下面Laplace算子的特征值和特征向量:

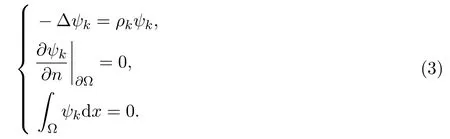
其中,ρk滿足:0<ρ1=ρ2<ρ3<ρ4=ρ5<ρ6=ρ7<ρ8≤···,且

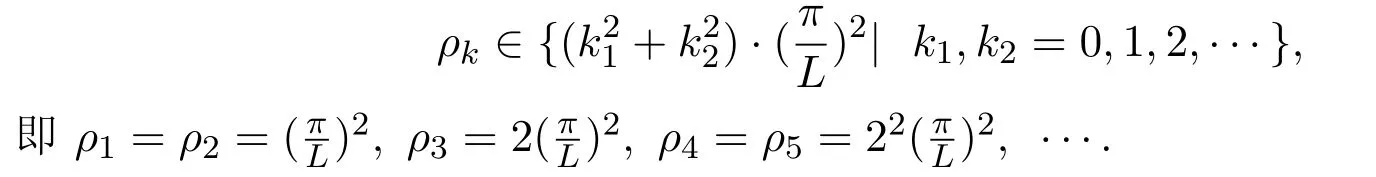
對應(yīng)的特征向量:

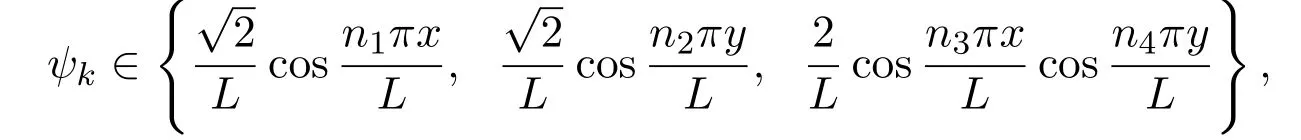
其中k,n1,n2,n3,n4=1,2,···,即

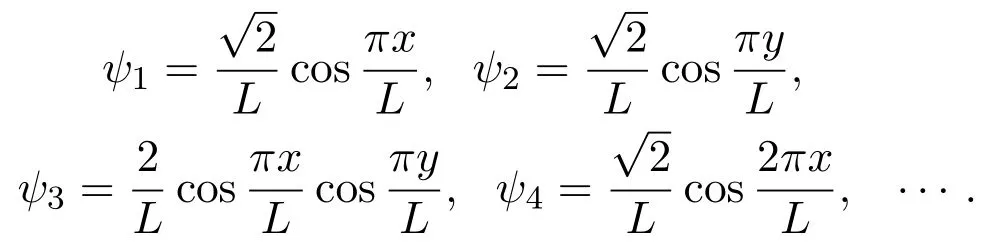
設(shè)Lλ的特征值和特征向量分別為,經(jīng)計算可得

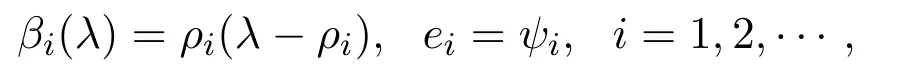
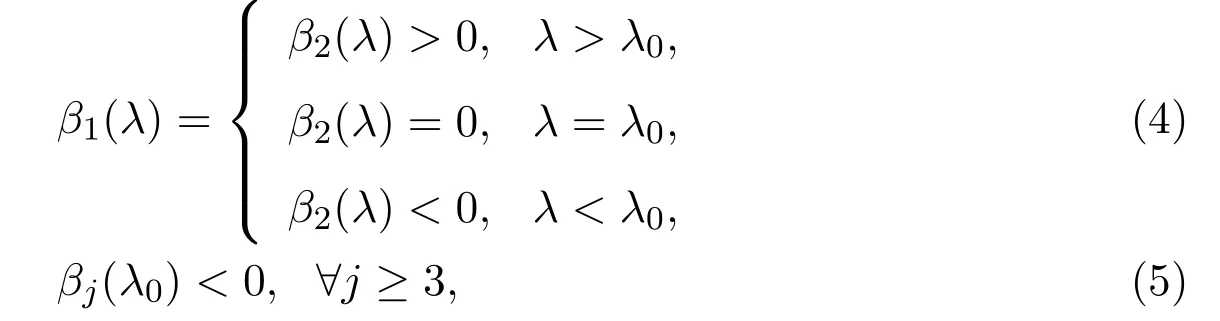
根據(jù)線性全連續(xù)場的譜理論,在λ=λ0的領(lǐng)域內(nèi)有如下的空間分解:

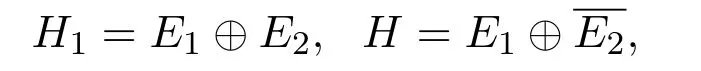
其中E1=span{e1,e2},E2=span{e3,e4,e5,···},

2為E2在H中的閉包,對任意u∈H1,存在

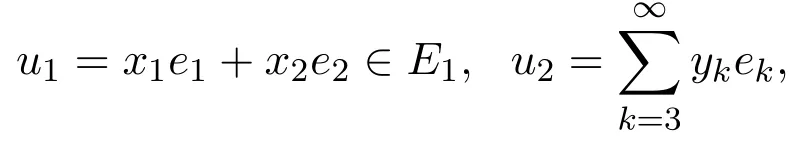
使得u=u1+u2.

2.3 定義及引理

定義 2.1令uλ∈X1是方程 (1)在λ=λ0處的分歧解,若Lλ+G(·,λ)在uλ處的導(dǎo)算子Lλ+DuG(uλ,λ):X1→X,在λ0的充分小的領(lǐng)域內(nèi)是線性同構(gòu)的,則稱該分歧解是正則的或非退化的.

引理 2.1每一個近似約化方程從λ=λ0處的非退化分歧解都唯一地對應(yīng)于原方程從λ=λ0處的非退化的分歧解.

引理 2.2假設(shè)條件(4)-條件(5)成立,若G(u,λ)有展開式

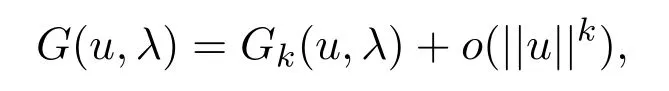
其中,k≥0為一整數(shù),Gk(u,λ)為k重線性算子,則方程(1)在λ=λ0附近的中心流形函數(shù) Φ:E1→E2可表達為其中,P2:H→E2為規(guī)范投影,

3 主要定理及證明

定理 3.1在條件(4)-條件(5)下,方程(1)有如下結(jié)論成立:

(iv)分歧出的分歧解可表達為:

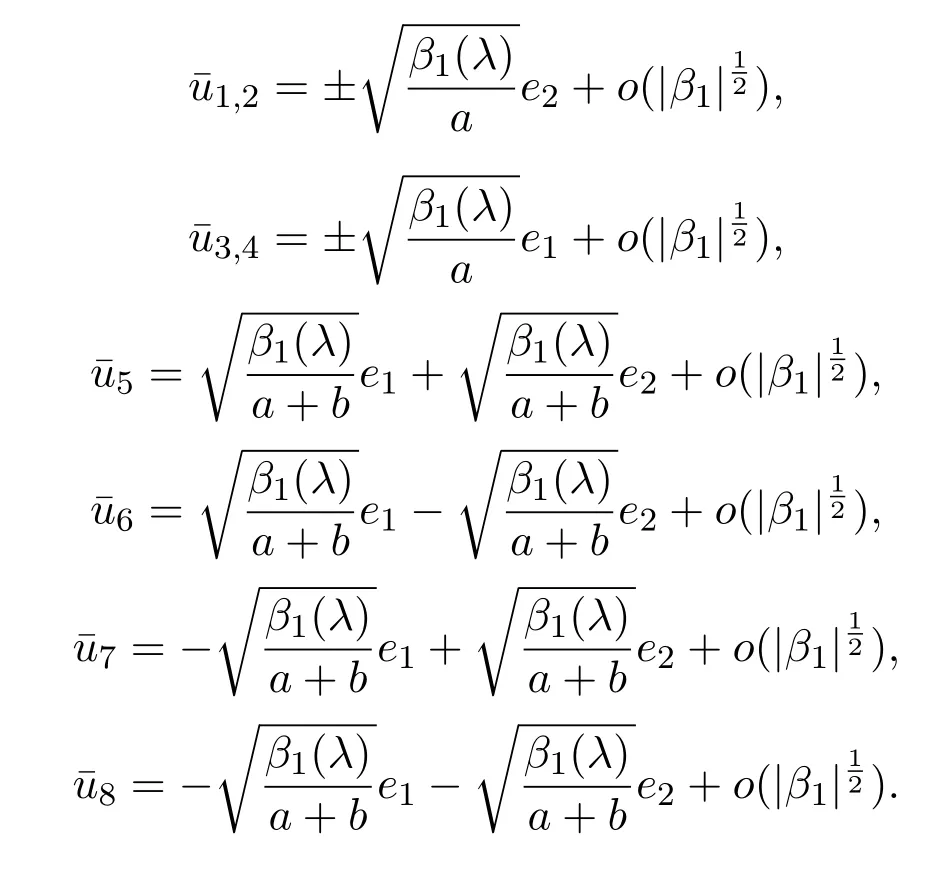
證明對方程 (1),由上一節(jié)的空間分解可知,?u∈H1,有u=u1+u2.假設(shè)u=u1+Φ(u1,λ),其中Φ(u1,λ):E1→E2為中心流形函數(shù).由 Lyapunov-Schmidt約化方法,知?ut,ei?=?Lλu,ei?+?G(u,λ),ei?,則方程 (1) 的分歧方程為:

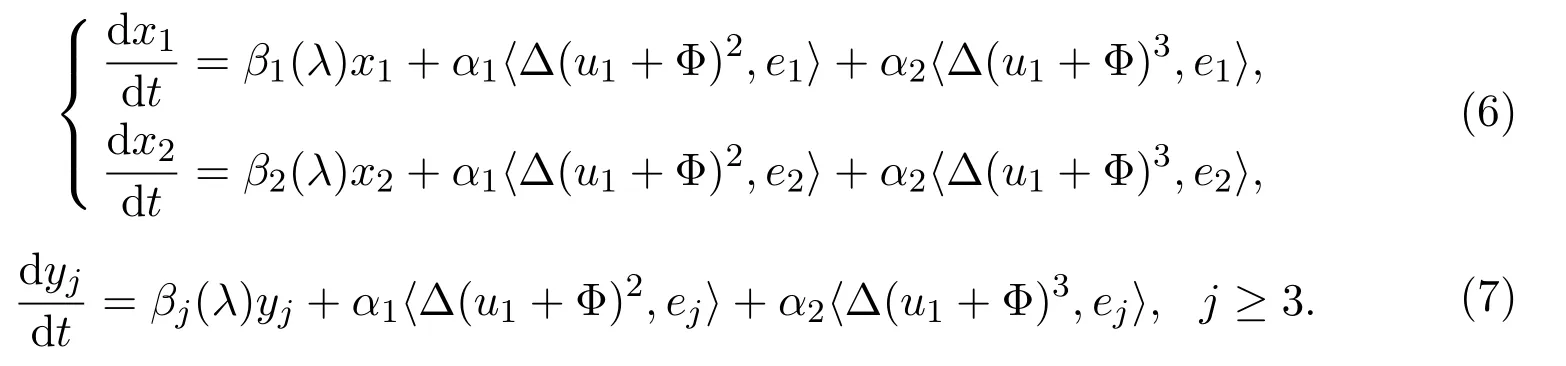
由計算可知

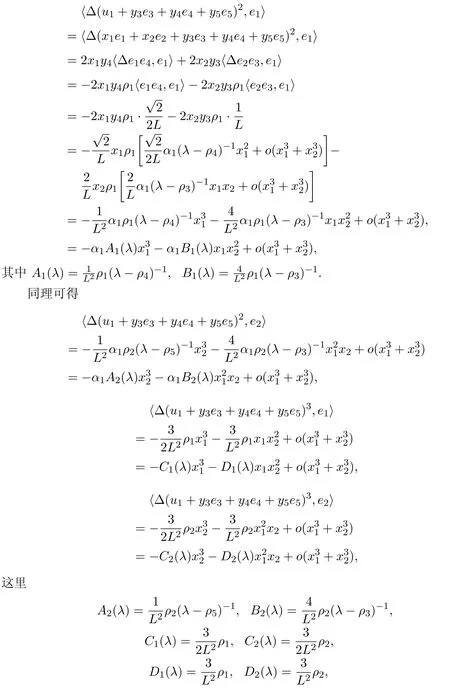
由此(8)式可化為

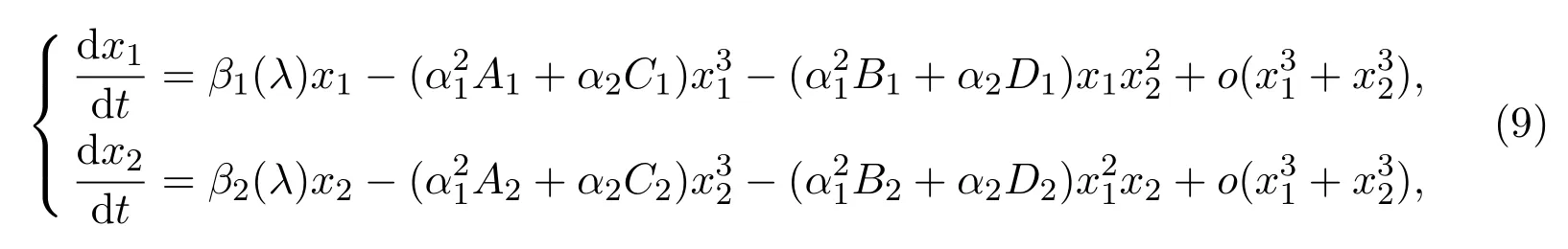
顯然A1(λ)=A2(λ),B1(λ)=B2(λ),C1(λ)=C2(λ),D1(λ)=D2(λ).

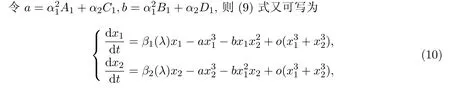
可解出方程(10)的近似解有如下八個:

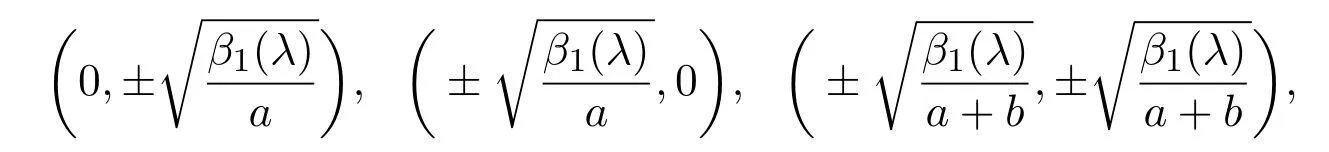
則方程(1)分歧出的分歧解為:

在λ0的充分小領(lǐng)域內(nèi),顯然有: