二次截面Nakayama代數的McCoy性

周玉業,程智

(安徽師范大學數學與統計學院,安徽 蕪湖 241003)

1 引言

在本文中,R是一個有單位元的環,R上的多項式環記作R[x],R上的n階矩陣環記作Mn(R).K是一個域,A為域K上的有限維代數.

文獻[1]指出所有的交換環都是McCoy環.后來,文獻[2-3]引入McCoy環的定義:如果對于任意的多項式f(x),g(x)∈R[x]{0},有f(x)g(x)=0,則存在r∈R{0},使得f(x)r=0(或rg(x)=0),那么環R稱為右 McCoy(或左McCoy)環.若一個環既是左McCoy環,又是右McCoy環,則該環稱為Mc-Coy環.McCoy環上的矩陣環未必是McCoy環.但是McCoy環上一些特殊形式的矩陣環仍然是McCoy環,而且兩者之間的McCoy性是等價的[4].考察哪些環類是McCoy環一直是大家關心的問題.文獻[5]提出了三個公開問題,其中有兩個問題都是考察某些環類是否是McCoy環.部分學者則是從McCoy環不同形式的擴張來構造新的McCoy環類[6-8].

本文將考慮二次截面Nakayama代數中的所有McCoy環.為方便起見,約定代數A是不可分解的,即A不可以寫成兩個代數的直積.記代數A的Jacobson根為radA,如果A/radA同構于有限個域K的直積,則代數A稱為基本(basic)的.一個熟知的結論是所有的有限維基本代數都同構于路代數KQ的商代數.這里Q=(Q0,Q1)是一個quiver,其中點的集合Q0以及箭向的集合Q1都是有限集.路代數KQ中的基是Q中的道路,乘法由道路連接給出.設I為A中所有箭向生成的理想,代數A=KQ/I2稱為二次截面Nakayama代數,其中Q是An型(即由n個點以及n?1個箭向組成的樹),或者是n-圈(即由n個點和n個箭向組成的圈).Nakayama代數A是自內射的充要條件是Q是一個n-圈.

Nakayama代數是一類常見的表示有限代數,這類代數一直是代數學者的研究熱點.例如文獻[9]就對Nakayama代數上的所有Gorenstein投射模進行分類,文獻[10]則考慮了Nakayama代數上的一些同調性質.本文主要給出以下結果.

定理 1.1二次截面Nakayama代數A是McCoy環的充要條件是A是自內射代數.

2 引理

首先給出更一般的結論并加以證明.設

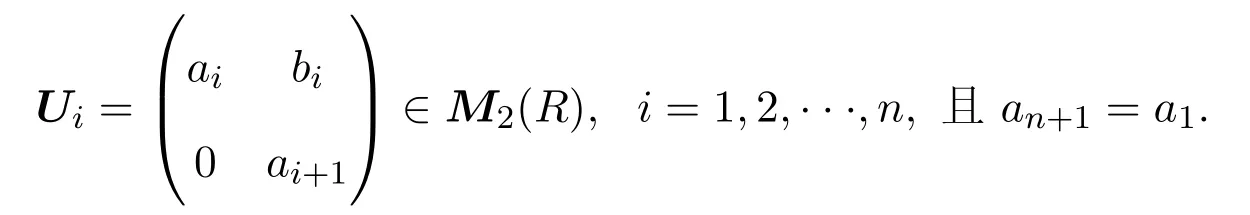
記V2n(R)是形如 Diag(U1,U2,···,Un)的對角分塊矩陣集合.不難證明,V2n(R)是M2n(R)的子環.

引理 2.1設R是有單位元的環,則R是右(或左)McCoy環當且僅當V2n(R)是右 (或左)McCoy環.

證明這里V2n(R)是M2n(R)的子環.我們直接驗證R是右McCoy環的情況,R是左McCoy環的證明方法類似.

(必要性)這里將V2n(R)中第i行,第j列元素為1,其余位置元素全部為0的2n階矩陣記作ei,j.為方便起見,也記ei,i為ei.設

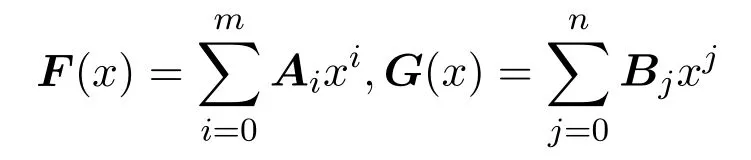
是V2n(R)[x]中的非零多項式,且滿足F(x)G(x)=0,其中

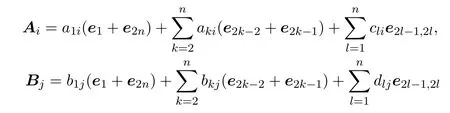
是V2n(R)中的矩陣.其中aki,bkj,cli,dlj是R中的元素,

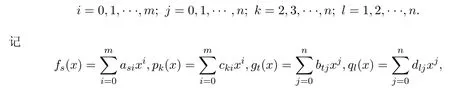
其中整數s,t,k,l=1,2,···,n.那么有

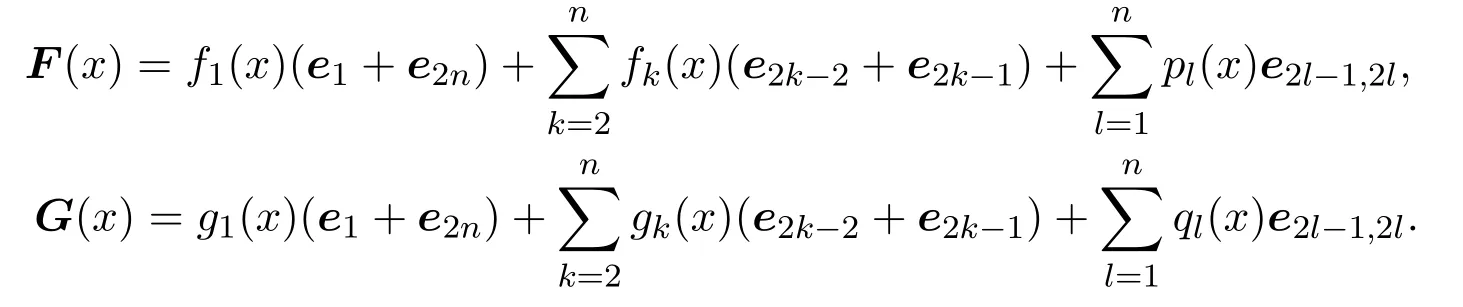
若有某個fs(x)=0.則存在S=e2s?1,2s,使得F(x)S=0.于是設fs(x)0,其中s=1,2,···,n.

情形 1gt(x)0,其中t是 1,2,···,n中的某個整數.

由F(x)G(x)=0,知ft(x)gt(x)(e2t?2+e2t?1)=0,則ft(x)gt(x)=0.這說明存在非零的rt∈R,使得ft(x)rt=0.因此F(x)rte2t?1,2t=0.

情形 2gt(x)=0,其中t是 1,2,···,n中的任意整數.

因為

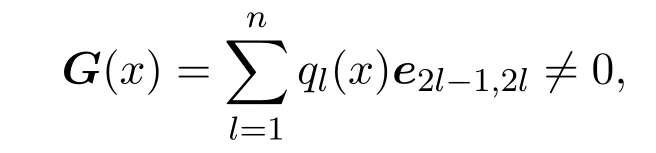
所以必有某個ql(x)0.根據F(x)G(x)=0以及V2n(R)的結構,可得到

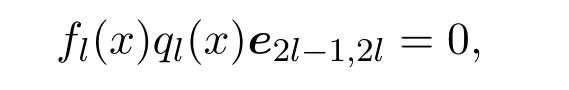
因而fl(x)ql(x)=0.這說明存在非零的rl∈R,使得fl(x)rl=0,因此

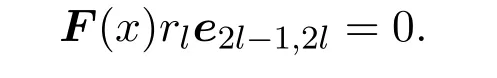
因此,V2n(R)是右McCoy環.

(充分性)設

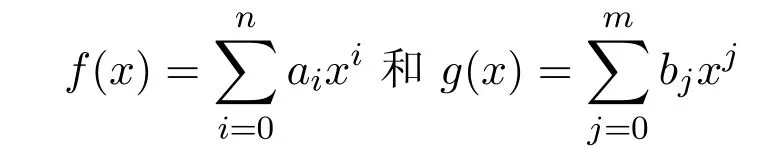
是R[x]中的兩個非零多項式,且滿足f(x)g(x)=0.記

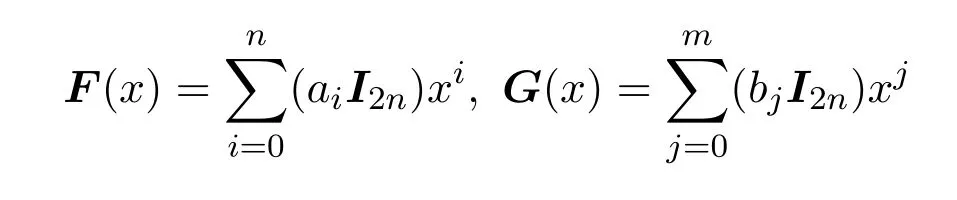
是V2n(R)[x]中的多項式,其中I2n是V2n(R)中的單位矩陣.因為f(x)0,g(x)0,所以F(x),G(x)都是非零多項式.又因為f(x)g(x)=0,所以

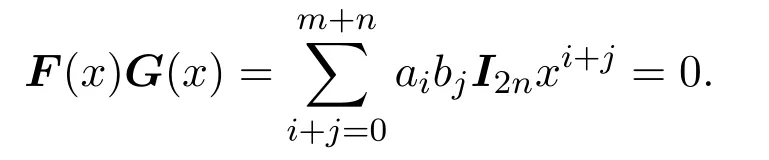
于是,V2n(R)是McCoy環說明了存在非零矩陣

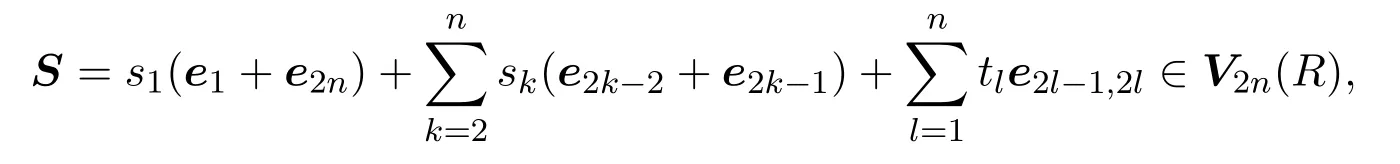
使得F(x)S=0,其中k,l=1,2,···,n是R中元素.若存在某個si0,則f(x)si=0.否則,由于0,則存在某個tj0,使得f(x)tj=0.因此,R是右 McCoy環.

若R是一個域,考慮以下的矩陣集合Tn+1(R).令

并記J為Tn+1(R)的Jacobson根,則有下面的結論.

引理 2.2環V2n(R)和Tn+1(R)/J2是同構的.

證明記ei,j是2n階矩陣V2n(R)中第i行,第j列元素是1,其余元素是0的矩陣.類似地,為方便起見,我們也將ei,i,Ei,i分別記為ei,Ei.

注意到V2n(R)中的所有矩陣可表達為如下形式:

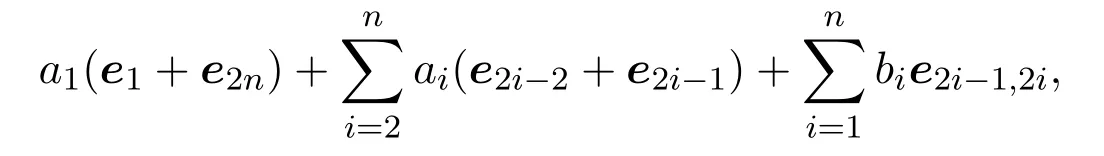
Tn+1(R)/J2中的所有矩陣可表達為如下形式:

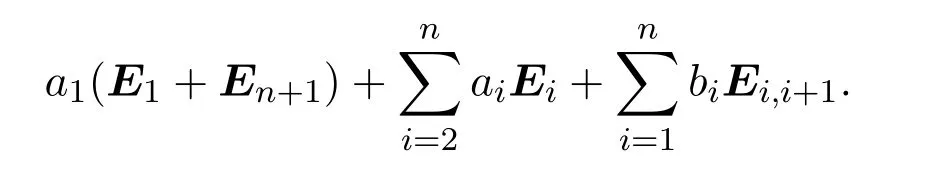
其中ai,bj∈R,i,j=1,2,···,n.

構造映射f:V2n(R)→Tn+1(R)/J2;x 7?→y.顯然,f是雙射.且對V2n(R)中的任意矩陣x,x′,可以直接證明f(x+x′)=f(x)+f(x′),f(xx′)=f(x)f(x′).因此f是環V2n(R)和Tn+1(R)/J2之間的一個同構.

3 定理證明

先證該定理的充分性:

注意到域 K是交換環,從而是 McCoy環.下面證明環Tn+1(K)/J2KQ/I2,Q是n個點的圈,I是由所有箭向生成的理想.記Q={Q0,Q1},Q0={1,2,···,n}是由n個點組成的集合,Q1={α1,···,αn?1,αn}是由所有箭向 (長度為1的道路)組成的集合,即對任意i=1,2,···,n?1,αi:i→i+1以及αn:n→1為Q中的所有箭向.注意到代數KQ/I2中的所有道路恰是長度為0的道路ωi,i∈Q0,以及Q1中的所有道路全體.于是KQ/I2中的元素x可表達為如下形式:

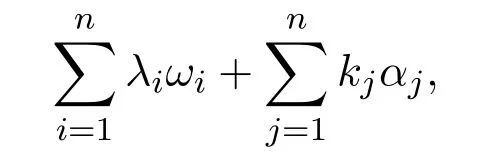
代數Tn+1(K)/J2中的元素y可表達為如下形式:

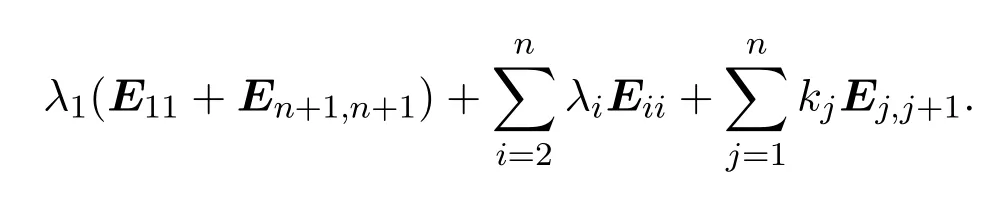
其中系數λ1,···,λn,k1,···,kn∈K.現構造g:KQ/I2?→Tn+1(K)/J2;.顯然g是映射且是雙射.

對于 KQ/I2中的任意元素x,x′,直接驗證知g(x+x′)=g(x)+g(x′).

注意到對 [1,n]中的任意整數i,j,若i=j,則ωiωj=ωi;若,則ωiωj=0,以及ωiαi=αi=αiωi+1.并且在環Tn+1(K)/J2中,Ej,j+1Ej+1,j+2=0.于是

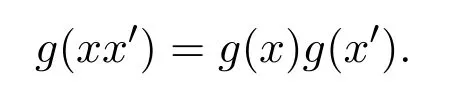
從而g是環KQ/I2到Tn+1(K)/J2的同構.

下證定理的必要性:

假設二次截面Nakayama代數A不是自內射的,則Q是An型的,即Q=(Q0,Q1),其中Q0={1,2,···,n},Q1={αi|αi:i→i+1,1≤i≤n?1}.

記B=KQ/I2,取B[x]中的兩個非零多項式