區間值映射的半連續性與凸性

李娜,包玉娥

(內蒙古民族大學數學學院,內蒙古 通遼 028043)

1 引言

區間值映射是取值為區間數的函數,是區間分析(區間數學)中的重要組成部分.為了建立區間值最優化理論[1-2]、區間值微分方程理論[3-4],人們開始討論區間值映射的可微性及凸性等問題,并建立了相關理論.

最優化理論作為數學的一個重要分支,有著廣泛的應用.然而在現實問題的建模過程中,由于一些數據或信息的不確定性,許多數學規劃中用區間數表示數據或信息的變化范圍[5-6].在討論區間值規劃的KKT最優性條件時區間值映射的凸性及相關性質起著關鍵作用[1,7-8].

文獻 [9-10]討論了區間值映射的極限及可微等問題,并給出了相關性質及其應用.本文在此基礎上,進一步討論區間值映射的半連續性及凸性問題.在第3節中,建立區間值映射的半連續性概念,并給出相關的性質.在第4節中,討論半連續區間值映射的凸性問題.

2 預備知識

本節介紹區間數及區間值映射的一些相關概念.

設 R表示實數集,對任意R且,稱有界閉區間為區間數,記為區間數全體構成的集合記為[R],并稱 [R]為區間數空間.特別是,對a∈R,記為=[a,a],則∈[R].當0時,稱為正區間數,其全體記為[R+],并稱為正區間數空間.下面首先介紹區間數空間[R]上的加法運算、數乘運算及大小關系[8,11].

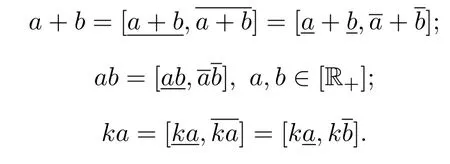
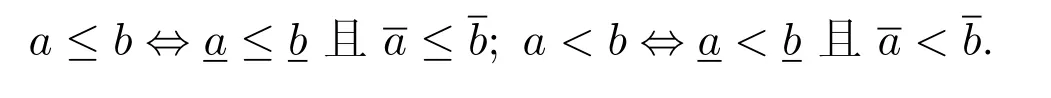
在上述序關系之下,易推出下面的結論.

引理 2.1設a,b,c,d∈[R],則

(1)a≤b?a+c≤b+c.

(2)a≤b?ka≤kb(k≥0).

(3)a≤b,c≤d?a+c≤b+d.

設M是n維歐式空間Rn的一個非空子集,映射F:M→[R]稱為區間值映射,且記為

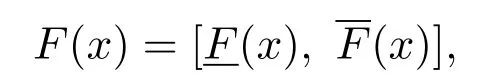
定義2.1[1,11]設M是n維歐式空間Rn的一個非空凸子集,映射F:M→[R]為區間值映射.若對任何α∈(0,1),有F(αx+(1?α)y)≤ αF(x)+(1?α)F(y),?x,y∈M,則稱F為M上的凸區間值映射.

引理 2.2[12]設M是n維歐式空間Rn的一個非空子集,若f是M上的實值函數且存在α ∈(0,1),使得f(αx+(1?α)y)≤ αf(x)+(1?α)f(y),?x,y∈M,則數集

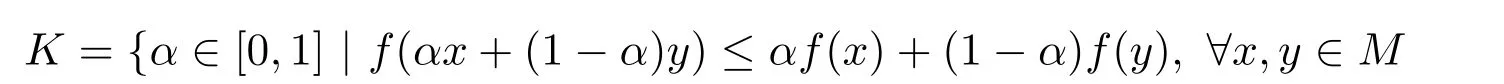
在[0,1]中稠密.

3 區間值映射的半連續性

本節主要引進區間值映射的半連續性概念及相關性質.為此,首先給出區間數空間子集的有界及確界的概念.

定義 3.1設A為區間數空間[R]中的非空子集.若存在區間數a∈[R],使得對任何x∈A,有x≤a,則稱a為A的一個上界,且稱A為有上界的子集.

設a0為A的一個上界,若對A的任何上界a,都有a0≤a,則稱a0為A的上確界,記作a0=supA.同理可以定義A的下界和下確界b0=infA.

若A既有上界又有下界,則稱A為有界集.

定理3.1若A為區間數空間[R]中的有界集,則A的上確界supA和下確界infA都存在,且supA=[supsup],infA=[infinf],其中.

證明設A為區間數空間[R]中的有界集,則存在,使得對任何x=[]∈A,有a≥x≥b,即且.所以由實數集的確界原理,有

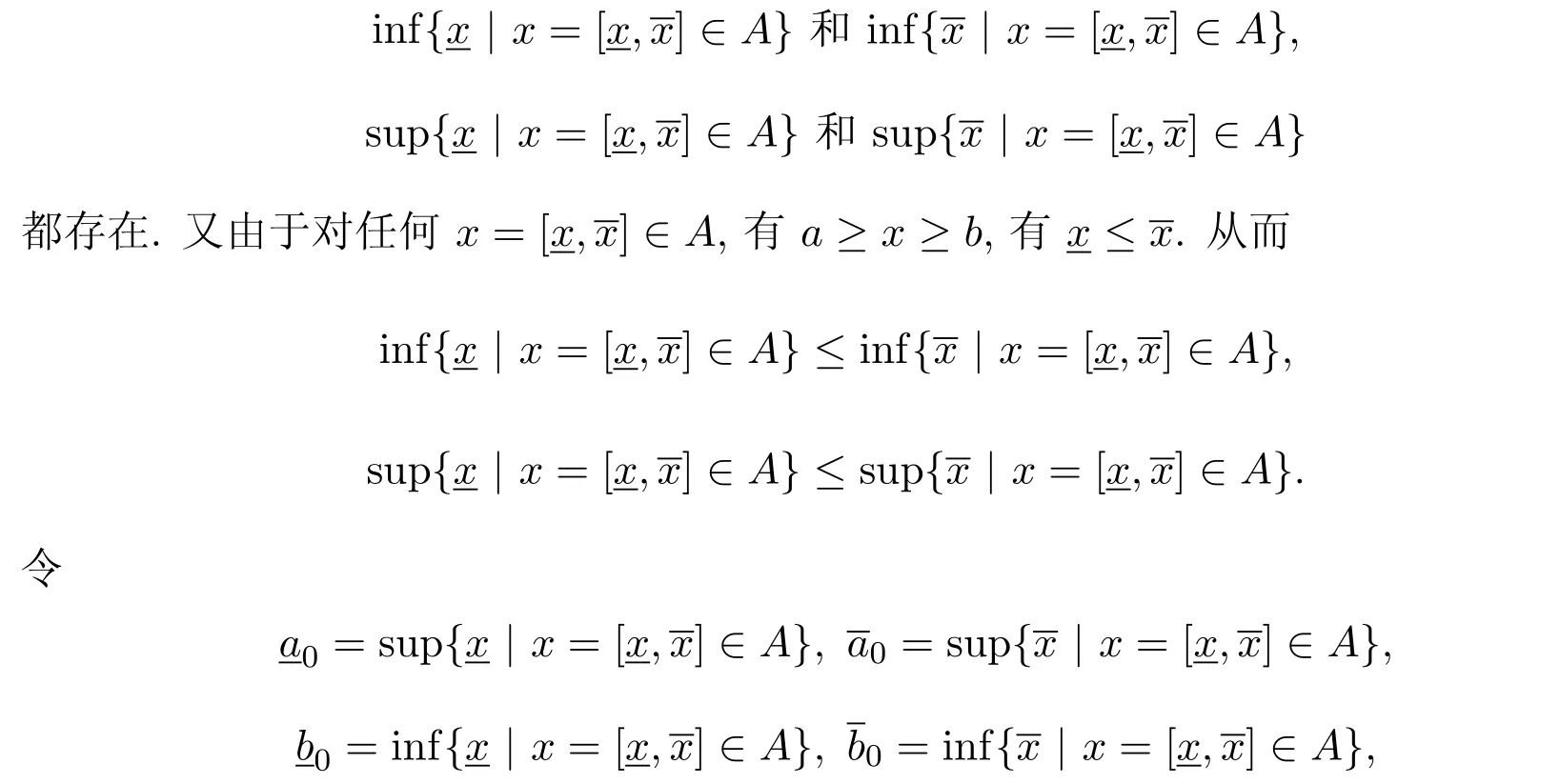
下面證明a0=supA=[supsup],b0=infA=[infinf].

只需證明a0=supA=[supsup]即可,b0=infA=[infinf]的證明類似.

假設a0supA,那么存在A的一個上界a1=[11]∈[R],使得a0>a1.從而01且01.又因為對任何x∈A,有x≤a1,即1且1.所以

這與0及0的定義相矛盾,故a0=supA=[supsup].

定義 3.2設F:M→[R]是一個區間值映射,x0∈M.如果對任意ε>0,存在δ>0,對任何x∈M,當‖x?x0‖<δ時,有,則稱F在點x0處下半連續.

如果F對M中的每一點都下半連續,則稱F在M上下半連續.

定理 3.2設F:M→[R]是下半連續的區間值映射,則實值函數(x)和(x)在M上下半連續.

證明設F:M→[R]是下半連續的區間值映射,x0∈M,則對任意ε>0,存在δ>0,當x∈M且‖x?x0‖<δ時,有F(x0)≤F(x)+.所以

從而由實值函數的半連續性概念,有實值函數(x)和(x)在M上下半連續.

定義 3.3設F是區間值映射,若存在A=[]∈[R],當x∈M時,有F(x)≤A,則稱F為有上界的區間值映射.如果存在B=[]∈[R],當x∈M時,有F(x)≥B,則稱F為有下界的區間值映射.

定理 3.3設M為閉集,F:M→[R]為下(上)半連續區間值映射,則F為有下(上)界的區間值映射.

證明設F:M→[R]為閉集M上的下半連續區間值映射,x0∈M,則對任意ε0>0,存在δ0>0,當x∈M且‖x?x0‖<δ時,有

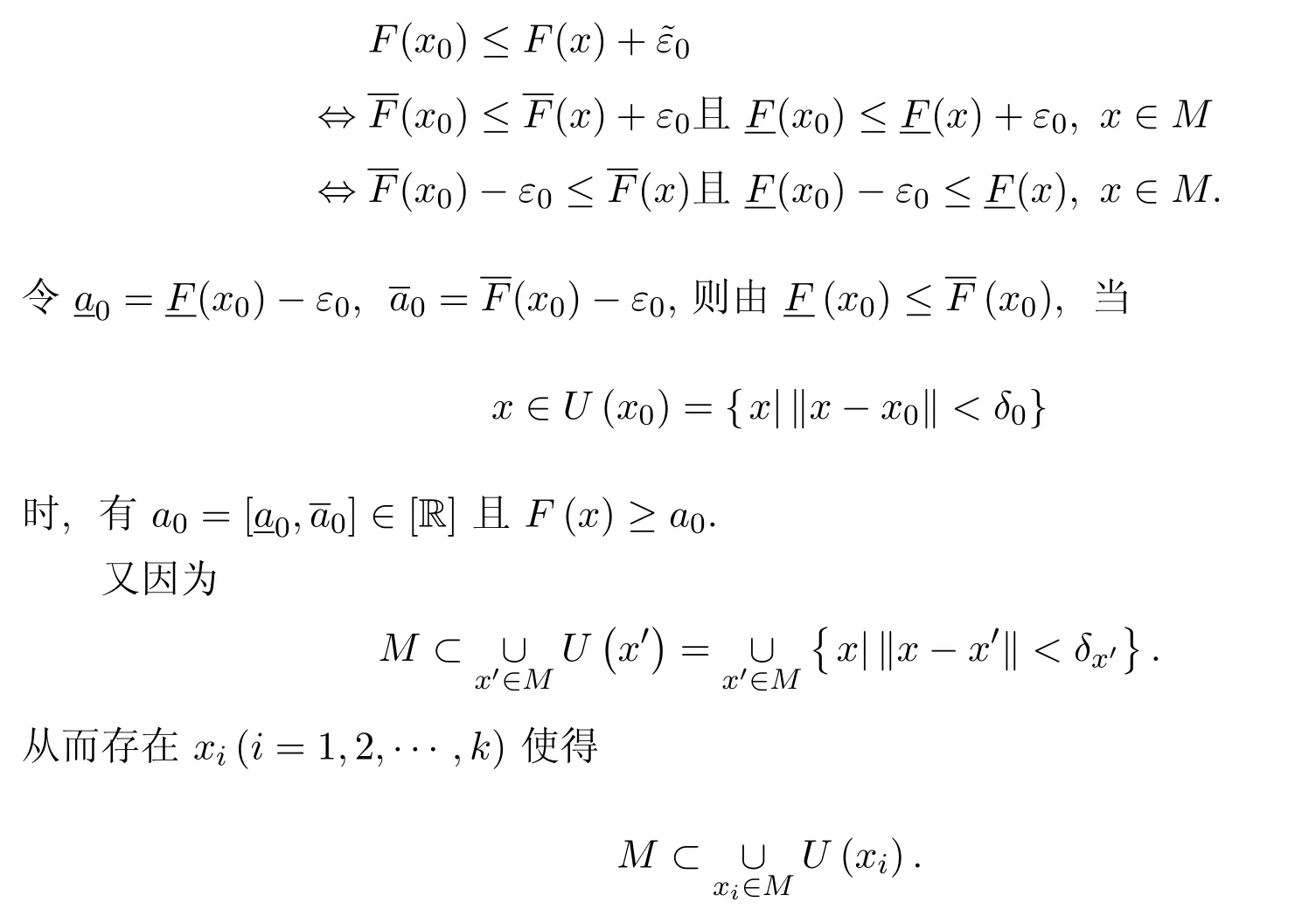
同理可證有界閉集的上半連續區間值映射有上界.

定理 3.4設F和G都是M上的上(下)半連續區間值映射,則F+G是M上的上(下)半連續區間值映射.

證明設F和G都是M上的上半連續區間值映射,x0∈M,則對任意ε>0,存在δ1>0,δ2>0,使得當x∈M且‖x?x0‖<δ1時,有

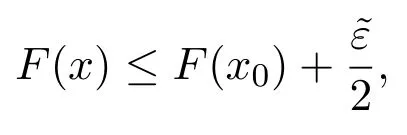
當x∈M且‖x?x0‖<δ2時,有

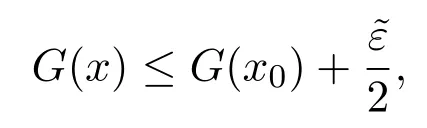
取δ=min{δ1,δ2},則當x∈M且‖x?x0‖<δ時,有

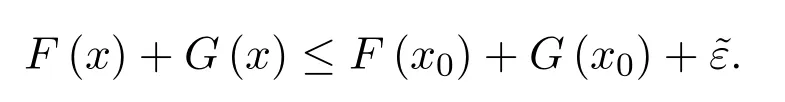
從而(F+G)(x)≤(F+G)(x0)+,即F+G是M上的上半連續區間值映射.

關于下半連續的情況證明類似于上半連續,從略.

稱F:M→[R+]為非負區間值映射,關于非負區間值映射有下面的結論.

定理 3.5設F和G都是M上的非負上半連續區間值映射,則F·G也是M上的上半連續區間值映射.

證明設F和G都是M上的非負上半連續區間值映射,對x0∈M及0<ε<1,令

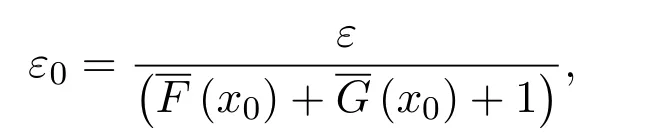
則 0<ε0<1且存在δ1>0和δ2>0使得當x∈M且‖x?x0‖<δ1時,有

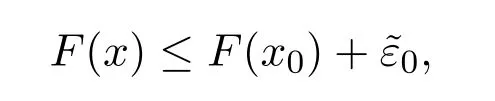
當x∈M且‖x?x0‖<δ2時,有

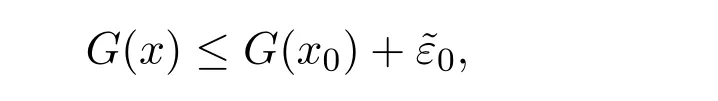
取δ=min{δ1,δ2},則當x∈M且‖x?x0‖<δ時,由F和G的非負性有

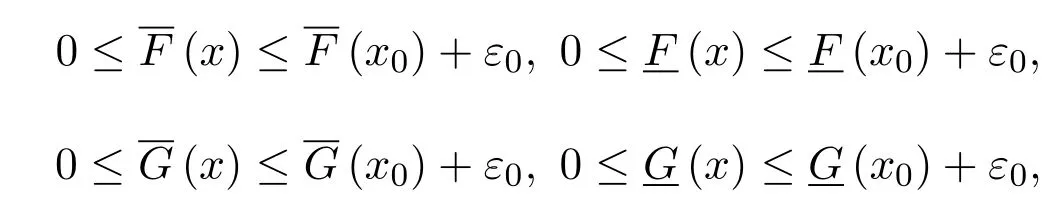
從而

4 區間值映射的凸性

本節討論半連續區間值映射的凸性問題.在本節中設M是n維歐式空間Rn的一個非空凸子集.首先將引理2.2推廣到區間值映射,給出下面的一個引理.

引理 4.1設F:M→[R]是一個區間值映射,如果存在α∈(0,1),使得

則數集

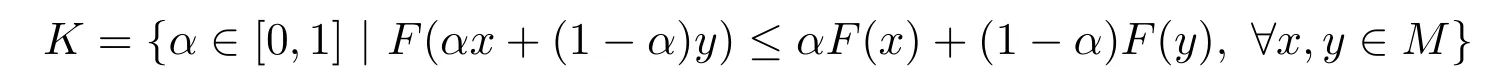
在[0,1]中稠密.

證明證明與文獻[12]中定理2的證明類似,從略.

定理 4.1設F:M→[R]是下半連續區間值映射,如果存在α∈(0,1)使得

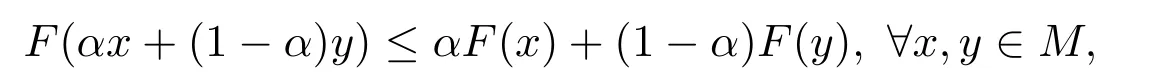
則F是M上的一個凸區間值映射.

證明對λ ∈(0,1),由引理 4.1可知存在點列λn∈K(n=1,2,···),使得

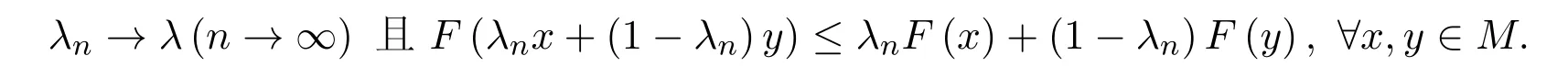
又由F的下半連續性及‖(λnx+(1?λn)y)?(λx+(1?λ)y)‖→0(n→ ∞)可得,對任意ε>0,存在N∈N+,當n>N時,有

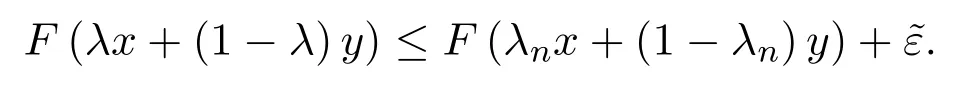
于是由λn∈K,有

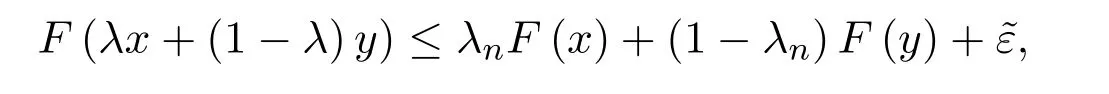
所以

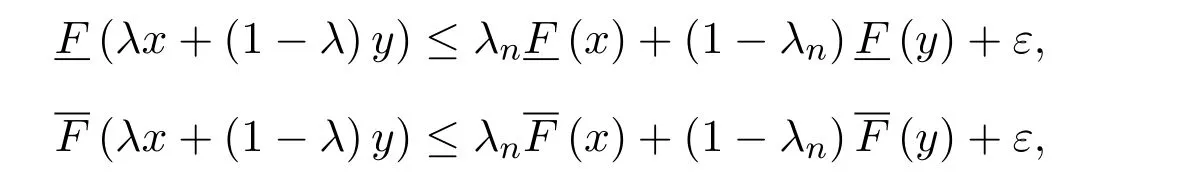
從而由ε的任意性,當n→∞時有

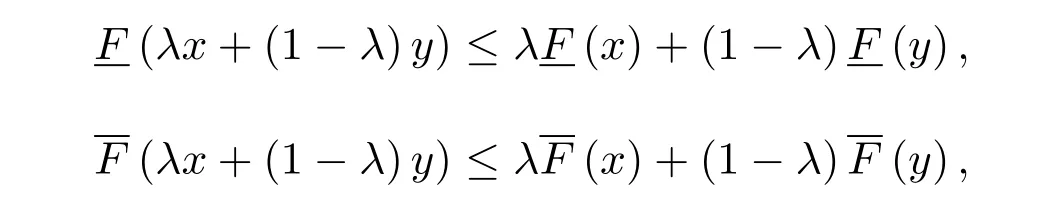
即

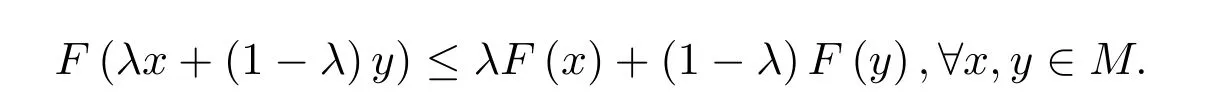
因此F是M上的一個凸區間值映射.

定理 4.2設F:M→[R]是上半連續區間值映射,如果存在α∈(0,1)使得

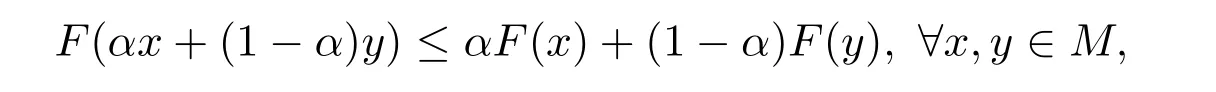
則F是M上的凸區間值映射.

證明對于λ∈(0,1),由引理4.1,可以選取單調遞增點列λn∈K(n=1,2,···),使得λn→λ(n→∞),則

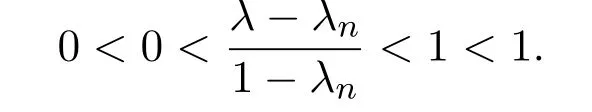
對x,y∈M,令s=λx+(1?λ)y,且

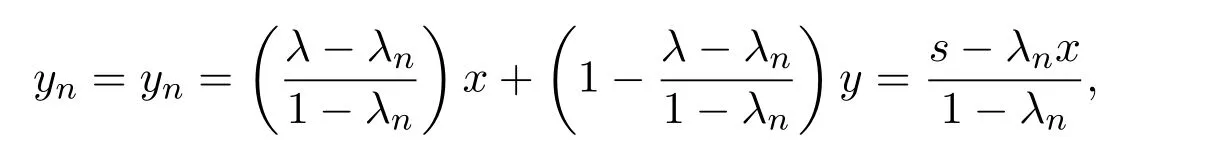
則s,yn∈M且

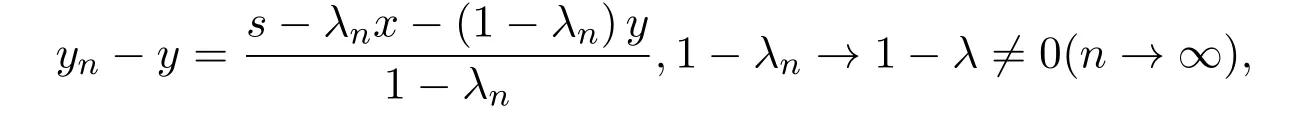
所以

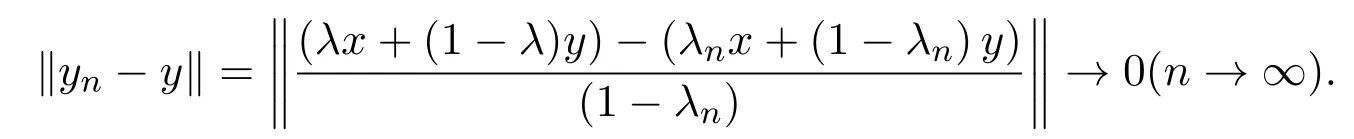
另一方面,對任意ε>0,存在N∈N+,當n>N時,有

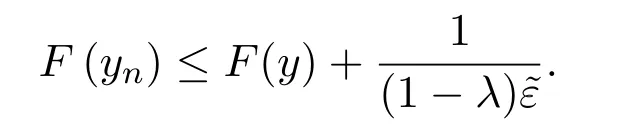
又由λn∈K,有

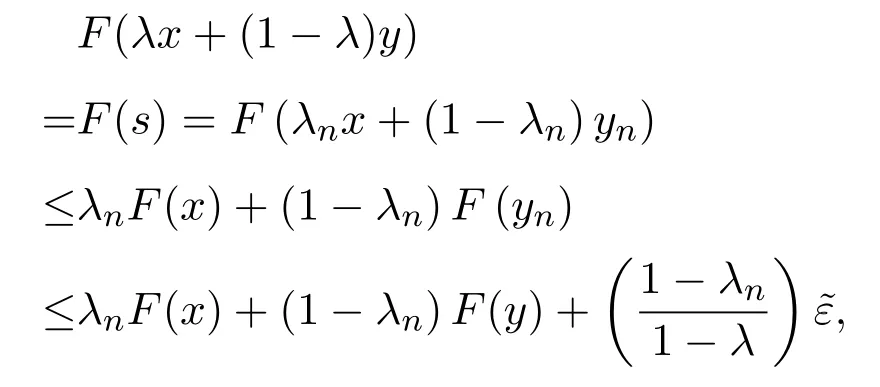
從而

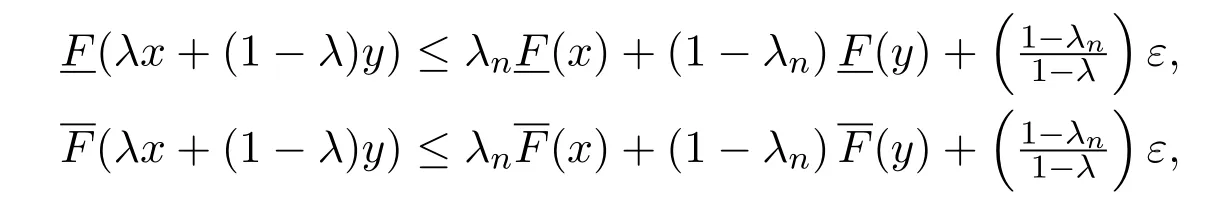
由ε的任意性,當n→∞時有

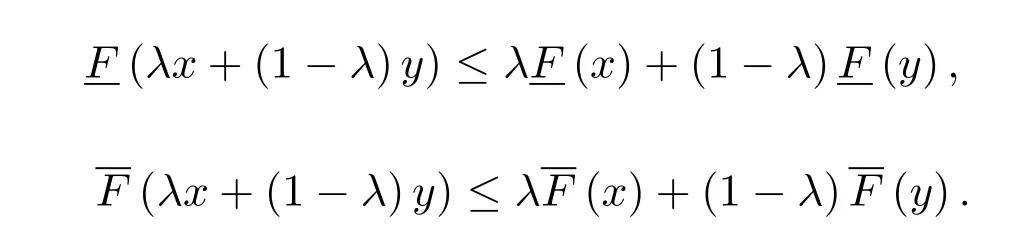
于是由區間數的序關系,有F(λx+(1?λ)y)≤λF(x)+(1?λ)F(y),?x,y∈M.因此F是M上的凸區間值映射.

定理 4.3設M是閉凸集,F:M→[R]是下半連續區間值映射.如果對任何x,y∈M,存在λ ∈(0,1)使得F(λx+(1?λ)y)≤ λF(x)+(1?λ)F(y),則F是M上的凸區間值映射.

證明設F:M→[R]下半連續,則由定理3.2,(x)和(x)是閉凸集M上下半連續的實值函數.于是由實分析的性質,(x)和(x)的上圖

都是Rn+1中的閉集.

如果對任何x,y∈M,存在λ∈(0,1)使得

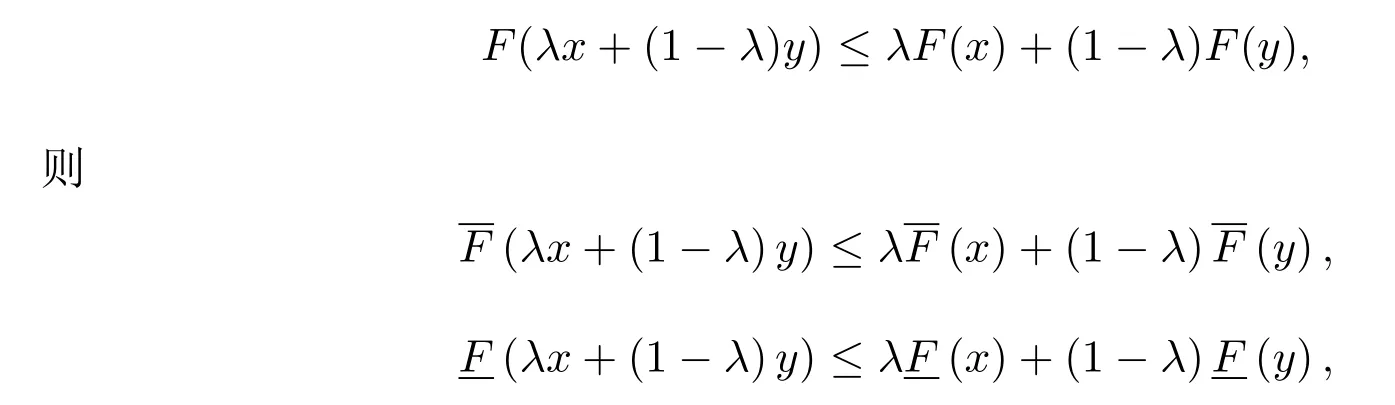
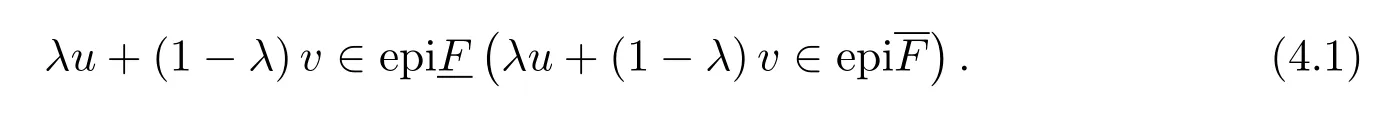
假設F:M→[R]不是凸區間值映射,則存在x,y∈M及λ0∈(0,1)使得

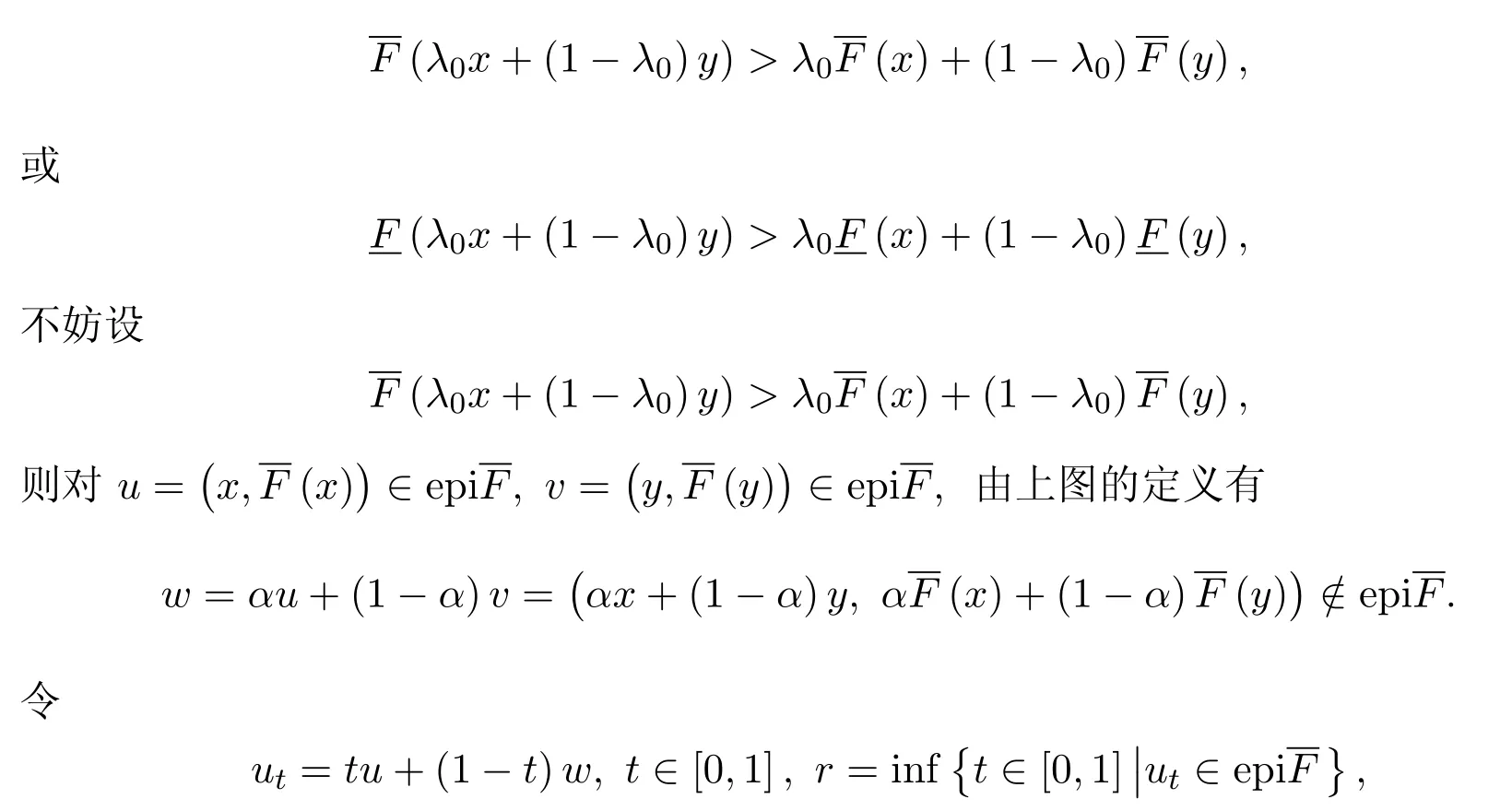
則存在{tn}∈[0,1]使得utn∈epi且tn→r(n→∞).于是由ut在點r∈[0,1]處的連續性及 epi的閉性,有ur∈epi.又由u0=epi,有r>0.從而當t∈[0,r),有utepi.

另一方面,令

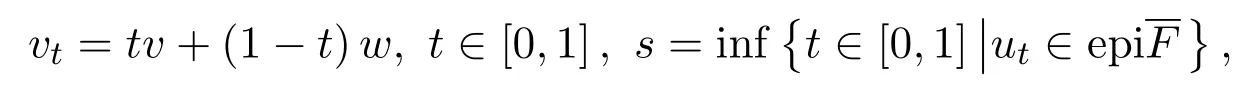
則同樣vs∈epi且s>0,使得當t∈[0,s)時,有vtepi.從而對任何λ∈(0,1),有

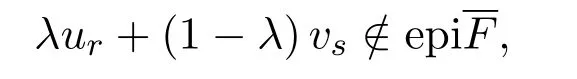
這與(4.1)式相矛盾.即F:M→[R]是凸區間值映射.

注 4.1在定理4.3中,當F:M→[R]是上半連續時,定理的結論也成立.