重溫知識(shí)發(fā)展之路，體驗(yàn)自主探索之趣
——“點(diǎn)到直線的距離”的溯源之旅

陜西

普通高中課程標(biāo)實(shí)驗(yàn)教科書在數(shù)學(xué)內(nèi)容編排上采取了“明確相關(guān)內(nèi)容在不同模塊中的要求及其前后聯(lián)系，注意使學(xué)生在已有知識(shí)的基礎(chǔ)上螺旋上升、逐步提高”的方式，利于學(xué)生學(xué)習(xí)循序漸進(jìn)、逐步發(fā)展，但也導(dǎo)致學(xué)生知識(shí)支離破碎，不利于構(gòu)建完整的知識(shí)體系.因此，教師應(yīng)該引導(dǎo)學(xué)生以居高臨下的態(tài)勢(shì)，以追溯賞析的方式，重溫知識(shí)的發(fā)生發(fā)展過(guò)程，體驗(yàn)自主探索的樂(lè)趣，幫助學(xué)生形成完整的知識(shí)體系.本文僅以“點(diǎn)到直線的距離”為例，談?wù)勔龑?dǎo)學(xué)生經(jīng)歷“溯源之旅”的初步認(rèn)識(shí).

一、“溯源之旅”案例賞析

1.“溯源之旅”的出發(fā)點(diǎn)

在《普通高中課程標(biāo)實(shí)驗(yàn)教科書·數(shù)學(xué)4(必修)》P99第二章平面向量學(xué)習(xí)中，教材給出了點(diǎn)到直線的距離公式的向量法證明，記為證法1.

證法1：如圖所示，P(x0,y0)是直線外一定點(diǎn)，M(x,y)是直線上任意一點(diǎn)，n0是直線l：Ax+By+C=0的法向量n=(A,B)的單位向量，

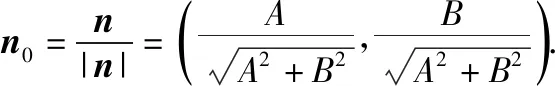
又點(diǎn)M(x,y)為直線l上任意一點(diǎn)，所以C=-(Ax+By),

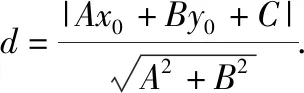
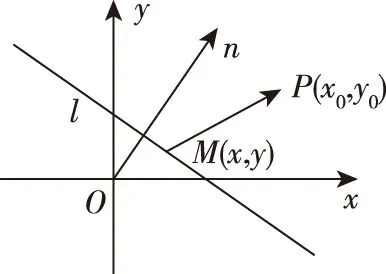
師：這種證法的本質(zhì)是什么呢？它與直線l上任意一點(diǎn)M(x,y)的選取是否有關(guān)呢？

生1：向量法是將點(diǎn)到線的距離問(wèn)題轉(zhuǎn)化成了直線上任意一點(diǎn)M與給定點(diǎn)P連線的向量在直線法向量上的射影的長(zhǎng)度，可簡(jiǎn)單地說(shuō)“射影的長(zhǎng)即距離”，它與直線上點(diǎn)P的位置無(wú)關(guān).

師：既然“射影的長(zhǎng)即距離”是該證法的本質(zhì)，那么是否一定要對(duì)直線的法向量單位化呢？

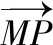
師：能否借助直線l的方向向量，求得點(diǎn)到直線的距離呢？

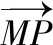
證法2：取直線l的方向向量為v=(B,-A)，則

又點(diǎn)P(x,y)為直線l上任意一點(diǎn)，所以C=-(Ax+By),

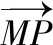
2.“溯源之旅”的追溯點(diǎn)

師：退一步想，求點(diǎn)到直線的距離最樸素、最自然的想法是什么呢？

生4：只需過(guò)點(diǎn)P作PH⊥l,垂足為H，先求直線PH的方程，從而可求出交點(diǎn)H的坐標(biāo)，再用兩點(diǎn)間的距離公式求|PH|.

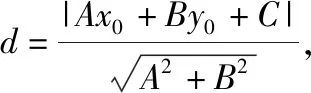
生5：我代表我們小組與大家分享我們組的證明方法，請(qǐng)大家提出寶貴建議.

過(guò)點(diǎn)P作PH⊥l于H(a,b)，則直線PH：Bx-Ay=Bx0-Ay0.

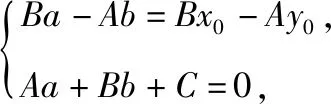
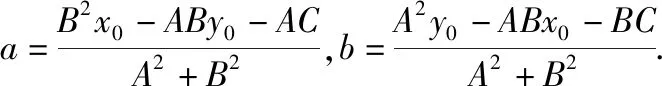
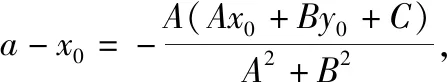
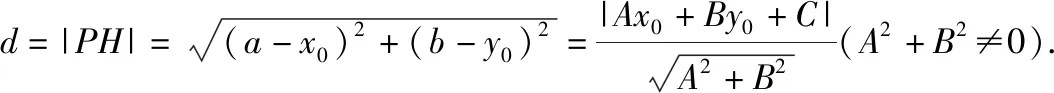
生6：我認(rèn)為用消元法解方程組時(shí)，需要對(duì)A，B是否為0進(jìn)行討論，同時(shí)，只需求得垂足H的橫坐標(biāo)a,再利用A(b-y0)=B(a-x0)直接求得b-y0的表達(dá)式更簡(jiǎn)潔.以下我代表我們組交流我們組的探究成果.

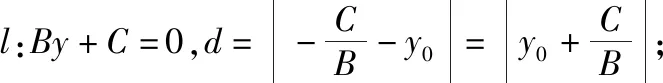
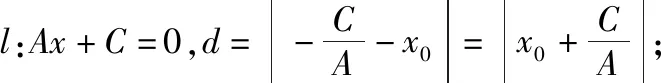
(3)當(dāng)A≠0,B≠0時(shí)，過(guò)點(diǎn)P作PH⊥l于H(a,b)，則直線PH：Bx-Ay=Bx0-Ay0.

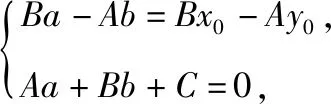
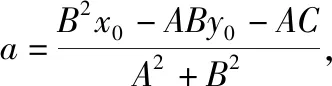
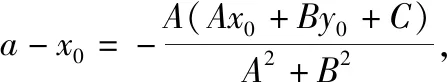
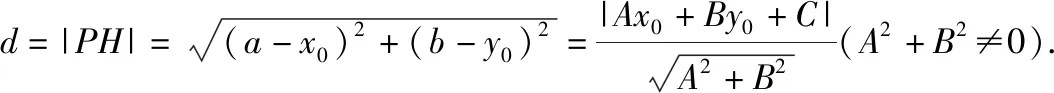
師：上述的方程和計(jì)算雖然稍顯繁瑣，但其中的分類討論、規(guī)范表達(dá)和多字母運(yùn)算的能力訓(xùn)練值得大家重視.當(dāng)然在具體計(jì)算和操作時(shí)，必然會(huì)受到字母參數(shù)過(guò)多及運(yùn)算過(guò)程復(fù)雜的困擾，這也正是大家能力提升的生長(zhǎng)點(diǎn).

師：證法3中導(dǎo)致運(yùn)算繁瑣的成因是什么？能否對(duì)證法作進(jìn)一步簡(jiǎn)化呢？

生7：我們組認(rèn)為，可從條件出發(fā)向(a-x0)和(b-y0)靠攏，于是，對(duì)第三種類型作如下改進(jìn).

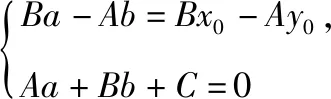
由①2+②2得(A2+B2)(a-x0)2+(A2+B2)(b-y0)2=(Ax0+By0+C)2,

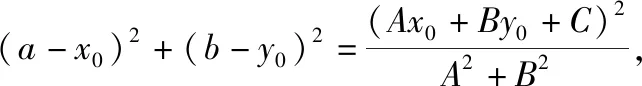
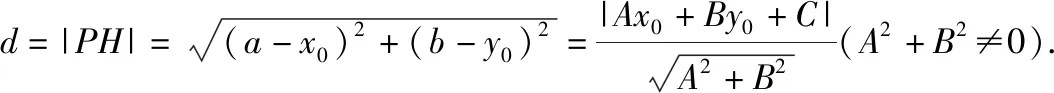
師：我們尤其要注意條件到結(jié)論的目標(biāo)意識(shí)和整體代換，證法4的表達(dá)和計(jì)算方式可能更符合大家的現(xiàn)實(shí)能力和水平，也有助于更好的突出條件到目標(biāo)的指向性，對(duì)提升大家方程變形和整體運(yùn)算能力很有教益.當(dāng)然，在以上的計(jì)算中，也可以利用換元法：

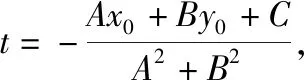
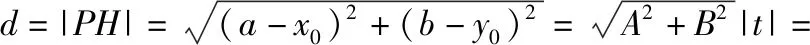
師：證法3、證法4都是利用解析法將幾何問(wèn)題代數(shù)化.我們能否利用直角三角形的面積公式來(lái)解決點(diǎn)到直線距離的求解呢？

證法5：(3)由A·B≠0知直線l必與兩坐標(biāo)軸相交，如圖，作PM∥x軸交直線l于M，作PN∥y軸交直線l于N，作PH⊥l于H，則d=|PH|.

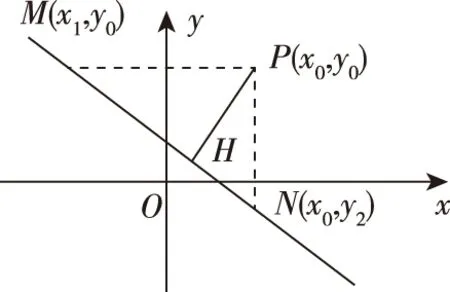
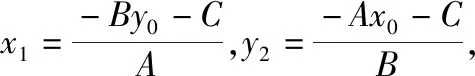
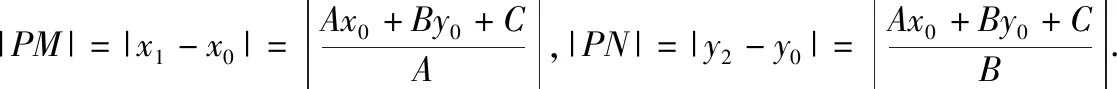
3.“溯源之旅”的生長(zhǎng)點(diǎn)

生8：老師，空間點(diǎn)到平面的距離有沒(méi)有類似公式呢？

師：生8這個(gè)“節(jié)外生枝”的類比聯(lián)想問(wèn)的好！解決了平面內(nèi)點(diǎn)到線的距離問(wèn)題，大家自然想到區(qū)別于《選修2-1》中向量法求空間點(diǎn)到面的距離的公式.

師：大家能否大膽想想平面方程是什么樣？空間點(diǎn)到平面的距離公式是什么樣？

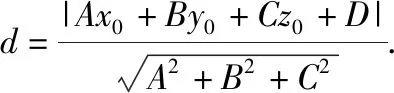
師：很好，這個(gè)僅依賴初等方法，根據(jù)《必修2》立體幾何初步中平面的確定條件、《選修2-1》空間向量等知識(shí)可得到證明.

平面內(nèi)點(diǎn)到線的距離可推廣到空間點(diǎn)到面的距離，并有如下基本結(jié)論：

(1)在空間直角坐標(biāo)系中，平面α的一般方程為Ax+By+Cz+D=0(A,B,C,D是不全為0的實(shí)數(shù))，則平面α的一個(gè)法向量n=(A,B,C).

證明：設(shè)平面α內(nèi)不共線三點(diǎn)為(xi,yi,zi)(i=1,2,3)，則

Ax1+By1+Cz1+D=0， ①

Ax2+By2+Cz2+D=0， ②

Ax3+By3+Cz3+D=0， ③

①-②

得A(x1-x2)+B(y1-y2)+C(z1-z2)=0， ④

①-③

得A(x1-x3)+B(y1-y3)+C(z1-z3)=0， ⑤

由④，⑤可知，(A,B,C)·(x1-x2,y1-y2,z1-z2)=0且(A,B,C)·(x1-x3,y1-y3,z1-z3)=0，

所以n=(A,B,C)是平面α的法向量.

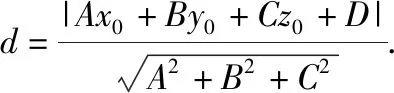
又點(diǎn)P(x,y,z)為平面α內(nèi)任意一點(diǎn)，所以D=-(Ax+By+Cz),

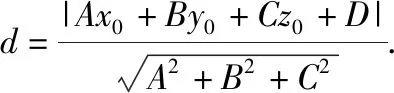
師：空間點(diǎn)到面的距離公式雖然涉及高等數(shù)學(xué)空間解析幾何知識(shí)，但我們?cè)诤锨橥评淼幕A(chǔ)上，用初等方法易于求出平面方程，得到了空間點(diǎn)到平面的距離公式.不難看出，空間點(diǎn)到面的距離公式是平面內(nèi)點(diǎn)到線距離公式的推廣，平面內(nèi)點(diǎn)到線距離公式是空間點(diǎn)到面距離公式的特例.

4.“溯源之旅”的落腳點(diǎn)

對(duì)于空間距離除幾何法、向量法、體積法外，公式法不失為一種有效的途徑.以下僅就點(diǎn)到平面的距離舉例，讓學(xué)生在自主探索中賞析品味用初等方法解決有高等數(shù)學(xué)背景問(wèn)題的樂(lè)趣.

例1.在底面邊長(zhǎng)與高都為2的正四棱錐P-ABCD中，試求底面中心O到側(cè)面的距離.

簡(jiǎn)析1：如圖，以底面中心O為原點(diǎn)建立空間直角坐標(biāo)系O-xyz，則A(1,1,0),B(-1,1,0),P(0,0,2),設(shè)平面PAB的方程為Ax+By+Cz+D=0，則將以上3個(gè)點(diǎn)的坐標(biāo)代入計(jì)算得A=0,B=-D,2C=-D，

所以平面PAB的方程為2y+z-2=0,

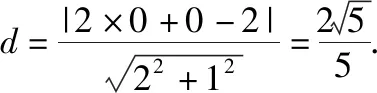
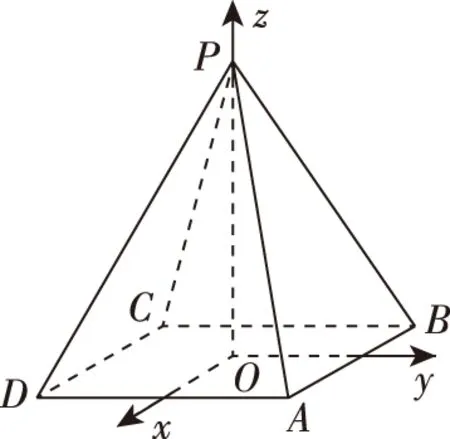
簡(jiǎn)析2：如圖，以底面中心O為原點(diǎn)建立空間直角坐標(biāo)系O-xyz，A(1,1,0),B(-1,1,0),P(0,0,2),設(shè)平面PAB內(nèi)任意一個(gè)動(dòng)點(diǎn)Q(x,y,z),則

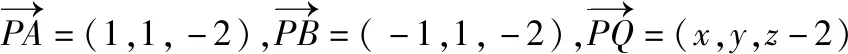
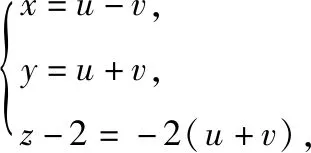
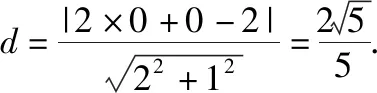
簡(jiǎn)析3：如圖，以底面中心O為原點(diǎn)建立空間直角坐標(biāo)系O-xyz，A(1,1,0),B(-1,1,0),P(0,0,2),設(shè)平面PAB內(nèi)任意一個(gè)動(dòng)點(diǎn)Q(x,y,z),則

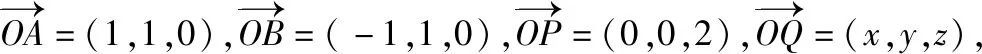
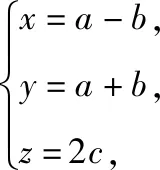
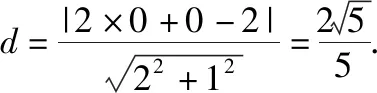
【評(píng)析】利用點(diǎn)到平面的距離公式求解，只需先求得平面的方程，然后用待定系數(shù)法、共面向量定理、空間向量基本定理等初等方法求平面方程運(yùn)算都很簡(jiǎn)便.

例2.如圖，在空間直角坐標(biāo)系中有單位正方體A1B1C1D1-ABCD.

(2)求點(diǎn)C1到平面A1BD的距離.

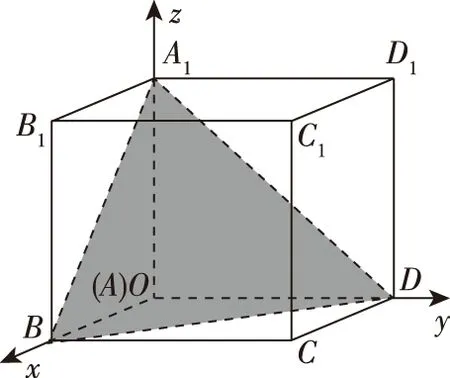
簡(jiǎn)析：(1)由題意有A1(0,0,1),B(1,0,0),D(0,1,0),C1(1,1,1).設(shè)平面A1BD的方程Ax+By+Cz+D=0，則將A1(0,0,1),B(1,0,0),D(0,1,0)三個(gè)點(diǎn)的坐標(biāo)代入計(jì)算得A=B=C=-D,

所以平面A1BD的方程為x+y+z-1=0,其法向量n=(1,1,1),

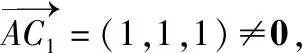
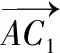
【評(píng)析】此解要用待定系數(shù)法求得平面A1BD的方程，本題兩問(wèn)可利用結(jié)論及距離公式同時(shí)解決.

例3.已知點(diǎn)M(-1,1,-2)，平面α過(guò)原點(diǎn)，且垂直于向量n=(1,-2,2),求點(diǎn)M到平面α的距離.

簡(jiǎn)析：由題意可設(shè)平面α的方程為Ax+By+Cz=0,則由n⊥平面α,可知

(A,B,C)=λn=(λ,-2λ,2λ)，

所以平面π的方程為x-2y+2z=0,

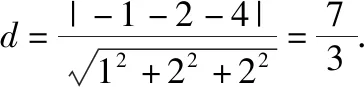
【評(píng)析】待定系數(shù)法求得平面方程，再利用點(diǎn)到平面的距離公式十分簡(jiǎn)捷.

二、“溯源之旅”的感悟

距離問(wèn)題是培養(yǎng)學(xué)生直觀想象、邏輯推理和數(shù)學(xué)運(yùn)算素養(yǎng)的很好載體.中學(xué)的距離問(wèn)題包括點(diǎn)到點(diǎn)的距離、點(diǎn)到線的距離、點(diǎn)到面的距離、線到線的距離、線到面的距離、面到面的距離和球面上兩點(diǎn)間的距離七大類型，它們之間可以相互轉(zhuǎn)化，其證明方法既可以用幾何法，也可以用向量法.對(duì)平面內(nèi)點(diǎn)到線的距離問(wèn)題，我們以向量法證明為出發(fā)點(diǎn)，追溯其最自然的算法，體驗(yàn)其中的解題思想，并將其推廣到空間，相關(guān)結(jié)論在解決空間距離中發(fā)揮了重要作用.經(jīng)歷了“點(diǎn)到直線的距離”的溯源之旅，學(xué)生對(duì)距離問(wèn)題的整體認(rèn)識(shí)有了進(jìn)一步的提高，對(duì)其中的數(shù)學(xué)思想和方法有了深刻的領(lǐng)悟.

荷蘭著名數(shù)學(xué)教育家弗萊登塔爾曾說(shuō)：“算法意味著鞏固,意味著由一個(gè)平臺(tái)向更高點(diǎn)的跳躍.”“溯源之旅”是引導(dǎo)學(xué)生對(duì)所學(xué)知識(shí)進(jìn)行“算法化”的思維躍升過(guò)程.因此，要立足提升學(xué)生的核心素養(yǎng)，遵循以下原則開(kāi)展有效的探索活動(dòng)：

1.發(fā)展性原則：通過(guò)探本溯源、理清聯(lián)系、明晰方向、預(yù)知未來(lái)，進(jìn)一步明確知識(shí)的發(fā)生、發(fā)展過(guò)程.

2.主體性原則：以學(xué)生為主體自主探究，引導(dǎo)學(xué)生經(jīng)歷探索全程，享受其中的樂(lè)趣.

3.完整性原則：選擇適宜的時(shí)機(jī)，保證一定的時(shí)間和空間，讓學(xué)生完整體驗(yàn)知識(shí)發(fā)生、發(fā)展過(guò)程，保證學(xué)生對(duì)知識(shí)模塊有一個(gè)較完整的認(rèn)識(shí).

溯源之旅中，隨著學(xué)生自主探究活動(dòng)的不斷展開(kāi)，新問(wèn)題不斷產(chǎn)生，教學(xué)成果往往超乎預(yù)設(shè)之外.這就需要教師靈活機(jī)智地、有針對(duì)性地指導(dǎo)、點(diǎn)撥、督促，讓學(xué)生在自主探索中充分經(jīng)歷知識(shí)的發(fā)生、發(fā)展過(guò)程，獲得最優(yōu)化的課堂學(xué)習(xí)效益.同時(shí)，教師對(duì)教材的理解和感悟，在很大程度上影響著預(yù)設(shè)水平和生成質(zhì)量，因而，教師的功底，也是一種體現(xiàn)教材和課標(biāo)指向的隱性預(yù)設(shè)，而這種最大的、全方位的預(yù)設(shè)成為教師引領(lǐng)溯源之旅的關(guān)鍵所在.