透視高考中的“平面折疊型”問題

安徽

所謂“平面折疊型”問題，即將平面圖形通過折疊變成立體圖形,讓靜止問題動態化,有效考查空間線線、線面、面面的關系，更有效考查空間角、空間距離、空間幾何體的體積與表面積，考查直觀想象、邏輯推理和數學運算等核心素養，使得對立體幾何的考查顯得更加豐富多彩.“平面折疊型”問題是近幾年高考和模考考查立體幾何的熱點，比如2016年和2018年全國卷解答題就有考查.下面結合典型試題予以介紹，供參考.

1.正方形中的折疊

【例1】如圖，在一個邊長為a的正方形S1S2S3S4內，有一個小正方形和四個全等的等邊三角形.將四個等邊三角形折起來，使S1，S2，S3，S4重合于點S,且折疊后的四棱錐S-ABCD的外接球的表面積是16π，則a=________.

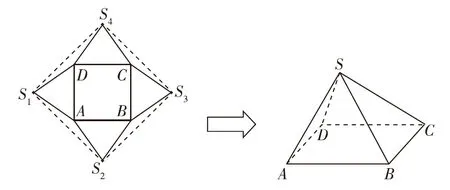
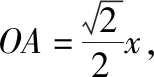
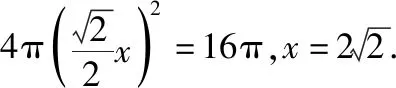
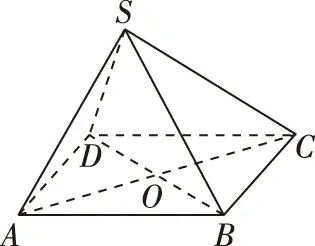
【評注】本題對正方形中的圖形進行折疊，形成一個所有棱都相等的特殊四棱錐.主要考查折疊問題的特征、特殊四棱錐外接球及其表面積計算等.注意所有棱都相等的特殊四棱錐，可以補成一個正八面體，其外接球的球心就是正方形ABCD對角線的交點.

2.等腰梯形中的折疊

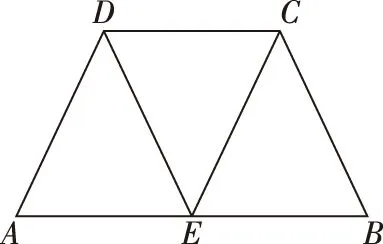
【例2】如圖，在等腰梯形ABCD中，AB∥CD,AB=2DC，E為AB的中點，將△ADE與△BEC分別沿ED，EC向上折起，使A，B重合于點P.

(Ⅰ)在折后的三棱錐P—DCE中，證明：PE⊥CD;

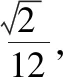
【解析】(Ⅰ)折后的三棱錐P—DCE如圖所示.取線段CD的中點F,連接PF,EF.在△PDC中，PD=PC,F是CD的中點，所以PF⊥CD.

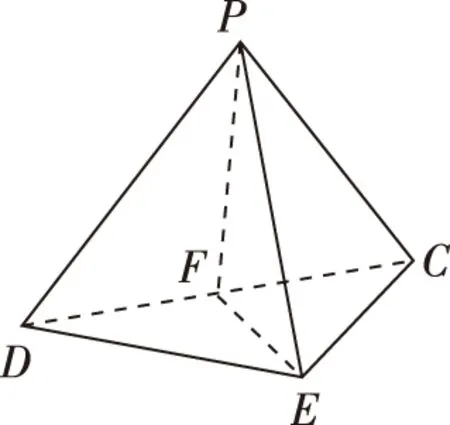
在△EDC中，ED=EC,F是CD的中點，

所以EF⊥CD.因此CD⊥平面PEF.

而PE?平面PEF，所以PE⊥CD.

(Ⅱ)當∠DEC=60°時，三棱錐P—DCE是正四面體，設其棱長為a.

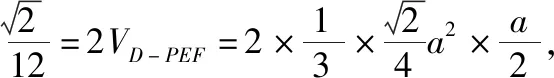
【評注】證明線線垂直、多面體的體積與表面積的計算，在平面折疊型問題中常常出現.

本題主要考查等腰梯形折疊成立體圖形、空間直線與直線、直線與平面、平面與平面之間的位置關系、由三棱錐的體積求表面積和平面幾何相關知識，體現對直觀想象、邏輯推理和數學運算三種核心素養的考查.本題折疊前后，不變的有ED=EC,PD=PC,△PDE全等于△PEC,但△PDE與△PEC的位置發生了變化.

3.正三角形中的折疊

【例3】如圖，正三角形ABC的邊長為a，將它沿平行于BC的線段PQ折起(其中P在AB邊上，Q在AC邊上)，使平面APQ⊥平面BPQC.D,E分別是PQ,BC的中點.

(Ⅰ)證明：PQ⊥平面ADE；

(Ⅱ)若折疊后，A，B兩點間的距離為d，求d的最小值.

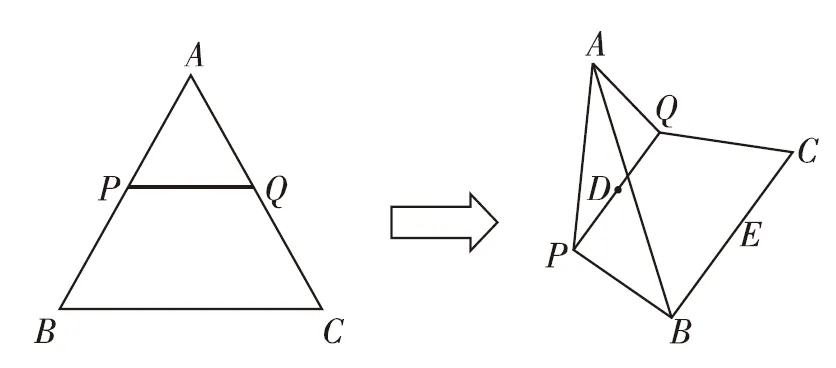
【解析】(Ⅰ)連接AD,DE,AE.在△APQ中，AP=AQ，D是PQ的中點，所以AD⊥PQ.又因為DE是等腰梯形BPQC的對稱軸，所以DE⊥PQ.

而AD∩DE=D,所以PQ⊥平面ADE.

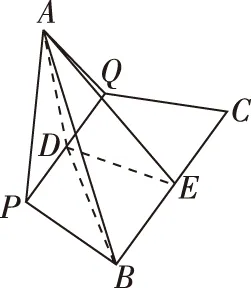
(Ⅱ)因為平面APQ⊥平面BPQC,AD⊥PQ，所以AD⊥平面PBCQ.連接BD，則d2=AD2+BD2.

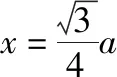
【評注】證明線面垂直、求點與點的距離在平面折疊型問題中常常出現.本題主要考查正三角形折疊成立體圖形、線面垂直的判定、面面垂直的性質、建立目標函數求最值，在圖形變化中考查直觀想象，在推理證明與建立函數中考查邏輯推理和數學運算.本題將正三角形折成了一個直二面角，折疊后的△APQ、梯形BPQC與折疊前的不變，只是位置發生了改變(垂直).A，B兩點間的距離發生了變化，且隨平行線PQ位置的變化而變化.因此要建立d關于x的目標函數，利用函數求d的最小值.

4.平行四邊形中的折疊

【例4】如圖，在平行四邊形ABCD中，4AB2+2BD2=1，AB⊥BD，沿BD將四邊形折成直二面角A-BD-C.

(Ⅰ)證明：AB⊥BC，CD⊥AD；

(Ⅱ)求三棱錐A—BCD外接球的體積.

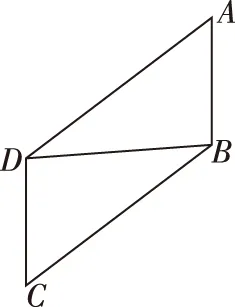
【解析】(Ⅰ)因為平面BDC⊥平面ABD，AB⊥BD，二面角A-BD-C是直二面角，

平面BDC∩平面ABD=BD,所以AB⊥平面BDC.

而BC?平面BDC,所以AB⊥BC.同理可得CD⊥AD.

(Ⅱ)取AC的中點O,則O是直角三角形ABC和直角三角形ADC斜邊的中點，

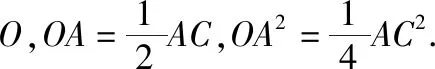
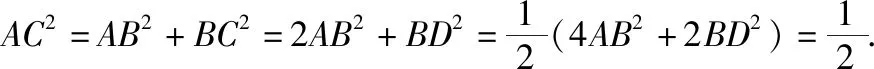
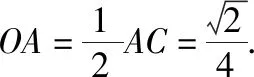
【評注】本題以特殊的平行四邊形為載體，主要考查折疊問題的特征、線線垂直的判定、線面垂直的判定與性質、面面垂直的性質、四面體外接球的體積計算等.這里的平行四邊形的一條對角線與一邊垂直，先注意正確畫圖，再利用折疊前后垂直不變性和度量不變性處理證明問題.通過觀察折疊前后位置關系與度量關系的變化情況,尋找三棱錐A—BCD外接球的球心是解題的關鍵.多面體的外接球問題是近幾年高考的熱點，常常與相關知識融合，具有背景新、結構新、解法新的特點，要引起足夠重視.

5.直角三角形中的折疊

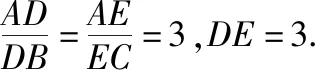
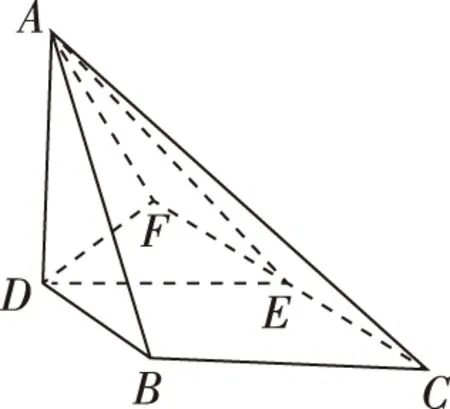
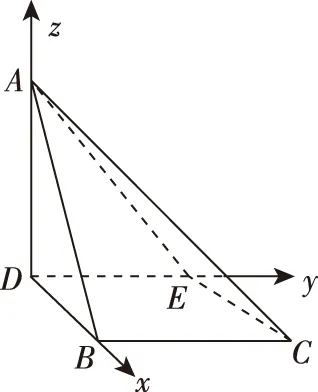
(Ⅰ)證明：AD⊥平面DBCE；

(Ⅱ)求二面角A-EC-B的余弦值.

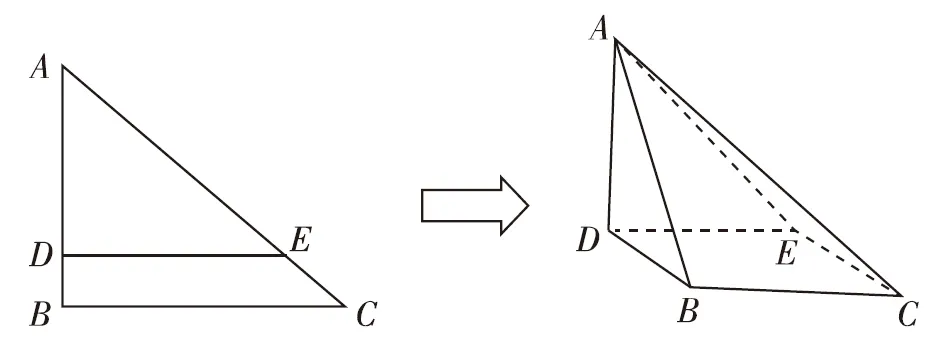
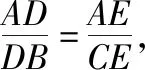
即∠ADB=90°,AD⊥DB.

而平面ADE∩平面DBCE=DE,所以AD⊥平面DBCE.

(Ⅱ)解法1(幾何法)：過D作DF⊥CE,交CE的延長線于F，連接AF.

易知AF⊥FC,因此∠AFD為二面角A-EC-B的平面角.

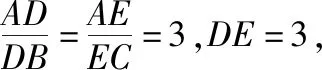
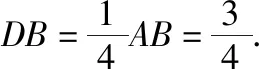
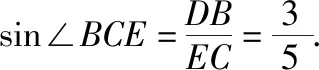
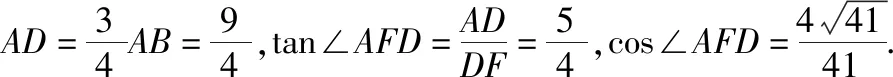
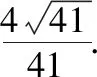
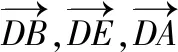
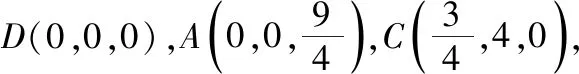
設平面AEC的法向量為m=(x,y,z),

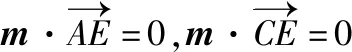
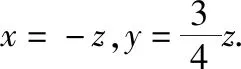
取m=(-4,3,4).又因為底面DBCE的一個法向量為n=(0,0,1),

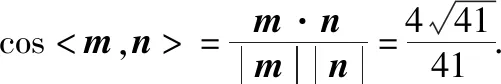
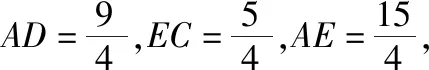
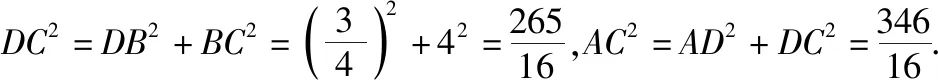
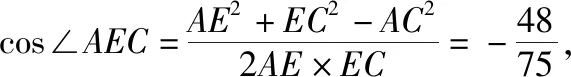
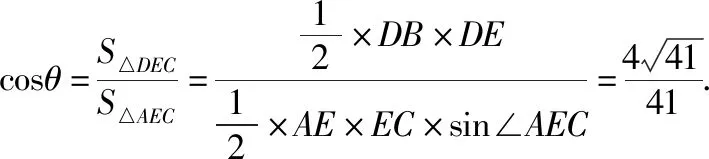
6.矩形中的折疊

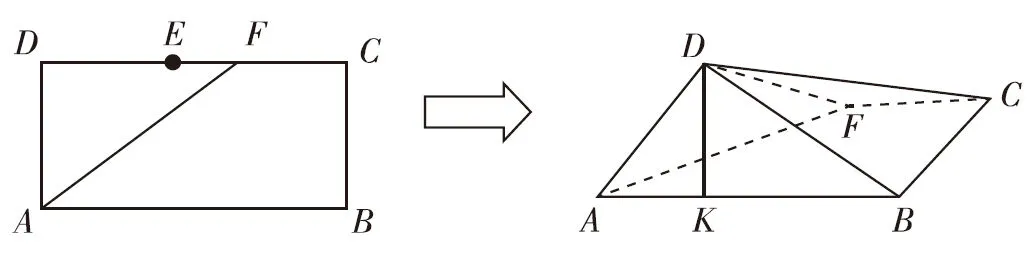
【例6】如圖，在矩形ABCD中，AB=2，BC=1，E為DC的中點，F為線段EC(端點除外)上一動點.現將△AFD沿AF折起，使平面ABD⊥平面ABC.在平面ABD內過點D作DK⊥AB，K為垂足.

(Ⅰ)證明：DK⊥AF；

(Ⅱ)設AK=t，EF=x,求t=f(x)的解析式，并確定f(x)的值域.

【解析】(Ⅰ)因為平面ABD⊥平面ABC,

平面ABD∩平面ABC=AB,DK⊥AB,AB?平面ABC,

所以DK⊥平面ABC.

又因為AF?平面ABC,所以DK⊥AF.

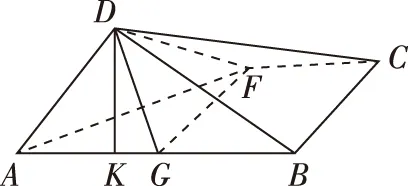
(Ⅱ)如圖，作FG⊥AB于G.因為EF=x,所以DF=1+x.

因為平面ABD⊥平面ABC,所以FG⊥平面ADB.

連接DG,則∠DGF=90°.

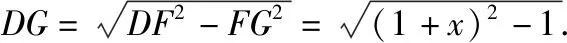
在Rt△DKG中,KG=AG-AK=DF-AK=1+x-t,

于是AD2-AK2=DG2-KG2,

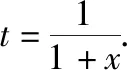
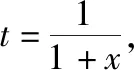
【評注】本題主要考查矩形折疊成立體圖形、空間直線與直線、直線與平面、平面與平面之間的位置關系、構建方程、建立目標函數等，有一定的難度.這里AB⊥BC，FC⊥BC不變,四邊形ABCF，三角形ADF各邊長不變，AD，BC，DC的位置有變化，線段DB，DC的長度有變化.