活用二級結論，巧解選填試題

湖南

通過基本性質、定理、公式推導出來并廣泛應用的結論性質被稱為“二級結論”.二級結論把程序性知識固化為結果性知識，形成知識組塊.二級結論的核心在于幫助學生在考試中迅速的利用一些“快準狠”的結論來解答一些問題，以實現分數快速提高.在高考數學復習中筆者發現，及時歸納并總結一些常用的二級結論，對于學生提高解題成功率、縮短運算時間非常有幫助.下面將高考試題中經常出現而且教材上有所體現的部分二級結論呈現給大家,部分結論對學生的解題有很好的指導作用,同時對演算結果有精準的驗證作用,以便同學們在解答高考題時做到準確、快捷.

一、函數問題中常用二級結論

結論一 奇函數的最值性質

已知函數f(x)是定義在集合D上的奇函數,則對任意的x∈D,都有f(x)+f(-x)=0.特別地,若奇函數f(x)在D上有最值,則f(x)max+f(x)min=0,且若0∈D,則f(0)=0.

【答案】2

【點評】奇函數的圖象關于原點對稱，那么它的最大值和最小值點肯定也關于原點對稱，也就是最大值和最小值互為相反數.本題型的解題方向就是設法將函數解析式進行分解，盡量分離出一個奇函數和常數或者具有單調性的部分，以達到速解目的.

結論二 抽象函數的對稱性

已知函數f(x)是定義在R上的函數.

【例2】已知函數y=f(2x+1)是定義在R上的奇函數，函數y=g(x)的圖象與函數y=f(x)的圖象關于直線y=x對稱，則g(x)+g(-x)的值為

( )

A.2 B.1

C.0 D.不能確定

【答案】A

結論三 周期函數問題

已知定義在R上的函數f(x),若對任意的x∈R,總存在非零常數T,使得f(x+T)=f(x),則稱f(x)是周期函數,T為其一個周期.

常見的與周期函數有關的結論如下:

1.如果f(x+a)=-f(x)(a≠0),那么f(x)是周期函數,其中的一個周期T=2a.

3.如果f(x+a)+f(x)=c(a≠0),那么f(x)是周期函數,其中的一個周期T=2a.

4.如果f(x)=f(x+a)+f(x-a)(a≠0),那么f(x)是周期函數,其中的一個周期T=6a.

5.若函數f(x)具有對稱軸x=a，x=b(a≠b)，則f(x)為周期函數且一個正周期為|2a-2b|.

6.若函數f(x)具有對稱中心(a,0)，(b,0)(a≠b)，則f(x)為周期函數且一個正周期為|2a-2b|.

7.若函數f(x)具有對稱軸x=a和對稱中心(b,0)(a≠b)，則f(x)為周期函數且一個正周期為|4a-4b|.

【答案】A

所以f(x)為偶函數.

于是f(1)+f(2)+f(3)=1+1-2=0，

所以f(1)+f(2)+…+f(2 019)=673×(f(1)+f(2)+f(3))=0.

【點評】函數的對稱性與周期性結論因為相似度高，運用時容易混淆.區分的關鍵是括號內x的系數符號“同號看周期，異號看對稱”.本題給出了對稱性和周期性的條件，需要分別利用對稱性和周期性結論，發現f(x)的奇偶性和周期性，進而得到問題的解答.

二、空間立體幾何中常用二級結論

結論四 多面體的外接球和內切球

2.已知三棱錐P-ABC，PA⊥平面ABC，若PA=a，△ABC的外接圓半徑為r，則該三棱錐P-ABC的外接球半徑R滿足(2R)2=(2r)2+a2.

3.棱錐的兩個側面互相垂直，已知兩個相互垂直的面的外接圓半徑的長及其公共棱的長度的情形：已知三棱錐A-BCD中，面ABD⊥面BCD，且△ABD，△BCD的外接圓半徑分別記為r1,r2，公共棱BD=a，則該三棱錐的外接球半徑R滿足：(2R)2=(2r1)2+(2r2)2-a2.

【例4】在《九章算術》中，將四個面都為直角三角形的三棱錐稱之為鱉臑.已知在鱉臑M-ABC中，MA⊥平面ABC，MA=AB=BC=2，則該鱉臑的外接球與內切球的表面積之和為________.

【解析】設MC的中點為O，如圖，

由AB=BC=2，且△ABC為直角三角形，得∠ABC=90°.

【點評】求多面體的外接球和內切球的策略不同，外接球盡量通過補形法或直接利用已有結論計算半徑(或者直徑)，而內切球常常利用等體積法來求.本題由條件不難看出球的直徑就是三棱錐的側棱MC，也可直接將三棱錐補形成正方體.而內切球的半徑由割補法，把三棱錐切割成以各面為底，球心為頂點的四個三棱錐，再利用三棱錐體積相等求半徑.

三、解析幾何中常用二級結論

結論五 焦點三角形的面積公式

( )

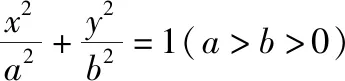
C.3 D.2

【答案】A

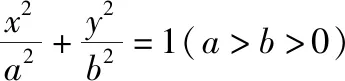
【點評】本題的巧妙之處在于利用橢圓與雙曲線的焦點三角形面積公式，得到橢圓的半短軸與雙曲線的半虛軸之間關系，再利用焦距相等，轉化成兩種曲線的離心率之間的關系，通過三角函數換元，進而求出橢圓和雙曲線的離心率的倒數之和的最大值.

結論六 圓錐曲線的切線問題

2.已知點M(x0,y0),拋物線C:y2=2px(p≠0)和直線l:y0y=p(x+x0).

(1)當點M在拋物線C上時,直線l與拋物線C相切,其中M為切點,l為切線.

(2)當點M在拋物線C外時,直線l與拋物線C相交,其中兩交點與點M的連線分別是拋物線的切線,即直線l為切點弦所在的直線.

(3)當點M在拋物線C內時,直線l與拋物線C相離.

【例6】已知拋物線C:x2=4y,若點P為拋物線C的準線上的任意一點，過點P作拋物線C的兩條切線PA,PB,其中A,B為切點,直線AB恒過定點為________.

【答案】(0,1)

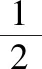
【點評】探究直線恒過定點問題，常常利用題設條件寫出目標直線的含參方程，由參數的任意性可得定點.利用圓、橢圓、拋物線已有切線結論，往往可以化繁為簡，達到速解目的.

結論七 圓錐曲線的中點弦問題

【例7】設直線l與拋物線C:y2=4x相交于A,B兩點，與圓(x-5)2+y2=r2(r>0)相切于點M，且M為線段AB的中點.若這樣的直線l恰有4條，則r的取值范圍是________.

【答案】2

【解析】當直線l的斜率不存在時，必有兩條垂直于x軸的直線和圓相切且滿足線段AB的中點為切點；

當直線l的斜率存在時，設斜率為k，A(x1,y1),B(x2,y2),x1≠x2,M(x0,y0),由上述結論得ky0=2.