凸顯聯系溝通構建數學模型

徐彬

【摘 ? 要】小學數學“解決問題”教學中，“回顧”即再現研究歷程，關注思路與結果的合理;“反思”即思考研究過程中的問題和策略，積累活動經驗，形成良好的認知結構。“回顧與反思”板塊的教學視角，分別是檢驗解決問題的結果、審視解決問題的思考過程、溝通方法之間的聯系、構建不同問題的數學模型。

【關鍵詞】解決問題;回顧與反思;聯系溝通;構建模型

一、背景陳述

人教版小學數學教材將“解決問題”分為三個教學板塊，即“閱讀與理解”“分析與解答”和“回顧與反思”。在日常教學中，教師往往重視閱讀與理解、分析與解答，而對于“回顧與反思”板塊，教學過程中則是簡略帶過，似乎可有可無。百度百科中，對于回顧、反思的解釋是：回顧指回想過去，思考過去發生的事件;反思指思考過去的事情，從中總結經驗教訓。而在小學數學“解決問題”教學中，“回顧”可以理解為再現研究歷程，關注思路與結果的合理;“反思”即進一步思考研究中的問題和策略，積累活動經驗，以形成良好的認知結構。

筆者曾執教《用方程解決問題》（人教版五年級上冊第五單元《簡易方程》P79例5）一課，特別關注“回顧與反思”板塊的設計與實施。為更好地了解學生的基礎，筆者對杭州市江干區220名五年級學生進行檢測（已學習過《用方程解決問題》一課）。

（一）檢測內容和目的

測試內容：甲地到乙地相距3000米，小王和小明兩人相向而行，小明每分鐘走80米，小王每分鐘走120米，問兩人幾分鐘后相遇？（請你把完整的解決過程表示出來）

測試目的：換一種問題情境，要求學生表示出用方程解決問題的完整過程，主要考查學生如何思考，能否解決問題。

（二）檢測數據和典型錯誤

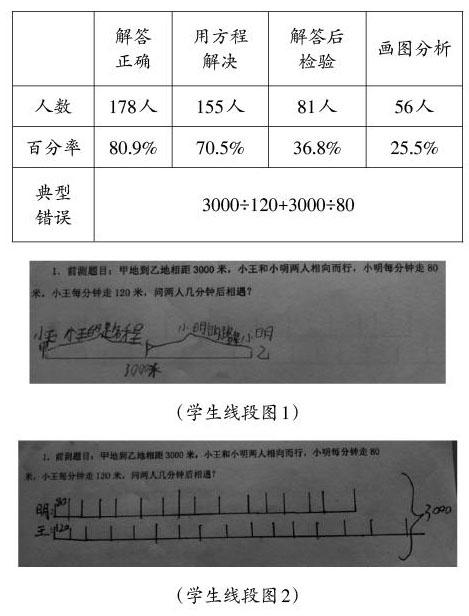
（三）檢測分析

關于“回顧與反思”的情況，分析可知：（1）學生缺乏檢驗的意識，題目明確要求表示完整解決問題的過程，僅有36.8%的學生進行了檢驗。（2）學生缺乏檢驗的方法，典型錯誤3000÷120+3000÷80，一個人行走都只需要25分鐘或37.5分鐘，兩人相向而行怎么會需要更多的時間，求出的答案明顯不合理。（3）情境改變后，部分學生沒有形成解決這類問題的模型，采用畫圖分析和檢驗的學生更是寥寥無幾。

基于上述分析思考，筆者在省、市、區教研員的指導下，重點對《用方程解決問題》“回顧與反思”環節展開教學研究，幾易其稿后，最終在研討活動中呈現了一個比較好的課堂結構，廣受好評。

二、實踐探究與反思

（一）檢驗解決問題的結果

在教材編寫上，對于解決問題檢驗的習慣培養是非常重視的，從低段開始，一年級上冊P46，就第一次呈現了“圖里有什么，怎么解答，解答正確嗎”。因此，在教學中，要有意識地培養學生檢驗的習慣，以提升學生解決問題的能力。常見的檢驗方法有3種：（1）估算，看看解決的結果是否合乎情理;（2）代入，把結果當成已知條件，檢驗結果是否與已知條件相符;（3）另解，用另一種方法解決問題，檢驗答案是否一致。

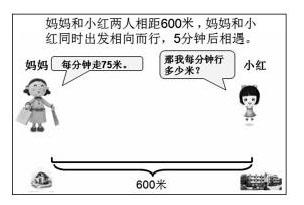
出示題目：“媽媽和小紅兩人相距600米，媽媽和小紅同時出發相向而行，5分鐘后相遇。媽媽每分鐘行75米，問小紅每分鐘行多少米？”學生在用多種方法解決問題后，教師這樣引導。

師：用方程解決問題，我們怎樣可以保證求得的結果一定是正確的？

生：檢驗。

師：是的，檢驗是必不可少的。怎么檢驗？

生：把45代入原方程進行檢驗。

生：這樣能保證這個方程的解正確，但不能保證問題解決是否正確。

生：把問題當成條件代入原來的題目中來算一算。

生：把小紅每分鐘行45米這個問題當成條件，求兩人相距多少米。

師：那就請你們自己動手來檢驗一下。

生：75×5+45×5=600（米），和原來條件兩人相距600米相一致。

生：（75+45）×5=600（米），和原來條件兩人相距600米相一致，前面解決問題的結果是正確的。

（二）審視解決問題的思考過程

張丹教授在《“問題解決”目標的內涵及實現》一文中提到，學生在問題解決中的失敗常常不是由于他們缺乏數學知識，而是由于他們不能有效地應用所學知識。好的問題解決者常常監控并調整他們解決問題的過程。

在“回顧與反思”環節，就要引導學生不斷去回顧解決問題的步驟和解決問題的策略。當然，這時候的回顧主體要明確，不是教師來回顧梳理，而應該是學生在經歷解決問題的基礎上通過反思，進一步明晰思考程序。

如在例題教學后，教師通過2個問題的驅動，引導學生回顧用方程解決問題的整個過程和加深對解決問題策略的感知，見以下教學片段。

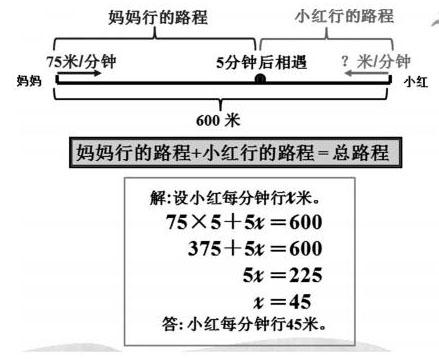
師：同學們很厲害，用兩種不同的方法解決了這個問題。我們來回顧一下，剛才是怎樣用方程解決問題的？

生：用方程解決問題，首先要找到等量關系—根據等量關系，設未知數列方程—解答并檢驗。

師：那有什么好辦法可以幫助我們找到等量關系呢？

學生通過回顧線段圖和等量關系的聯系，感受通過畫線段圖可以清楚地分析數量之間的相等關系，初步形成“畫圖分析—找等量關系—列方程”的一般過程，進一步深化畫圖解決問題的策略。

（三）溝通方法之間的聯系

眾所周知，用方程解決問題的關鍵是正確理解題意，快速有效地找到等量關系，然后根據等量關系列出方程。在平時教學中，學生常常對復雜的題目無從下手，因為他們不會主動去寫出等量關系，對于等量關系的重要性感受不夠。本課巧用“回顧與反思”環節，讓學生把結果當成條件代入原題進行編題檢驗，形成多個問題。通過變式編題討論，既進行了基本練習鞏固，更讓學生通過每個問題2種方法的比較和4個問題方法之間的溝通，感受到用方程解決問題的等量關系的一致性。

1.變式改編

師：前面檢驗中，同學們把小紅的速度每分鐘45米當成已知條件，可以算出總路程，你覺得還能解決什么問題？

學生編出：“媽媽和小紅相距600米，媽媽和小紅同時出發相向而行，5分鐘后相遇，小紅每分鐘行45米，問媽媽每分鐘行多少米？”

“媽媽和小紅相距600米，媽媽和小紅同時出發相向而行，媽媽每分鐘行75米，小紅每分鐘行45米，問幾分鐘后相遇？”

2.嘗試解決，基本鞏固

學生解決問題后，全班交流，通過列方程得出媽媽的速度是75米/分鐘，相遇的時間是5分鐘，和原來的條件是一樣的，也可以檢驗出我們前面解決問題的結果是正確的。

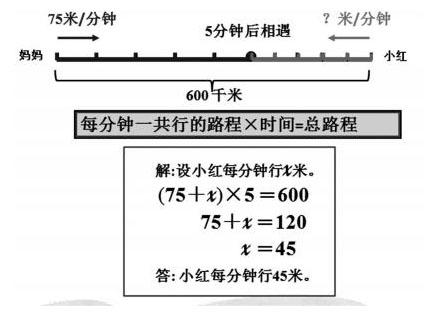
3.觀察比較，感受等量關系的重要性

師：我們剛才解決的這些不同的問題，有什么是相同的？

學生討論交流后，進一步理解每個問題的2種方法，明確各自的數量關系。還發現，同一情境下的4個問題，它們的基本等量關系是相同的，都是利用“媽媽的路程+小紅的路程=總路程”或“速度和×相遇時間=總路程”。一個等量關系可以解決這么多問題，讓學會體會到用方程解決問題的優越性。

（四）回顧與反思，構建不同問題的數學模型

周玉仁教授指出，小學生在解決問題的過程中，實際上完成了認識上的兩個轉化。第一個轉化指從紛亂的實際問題中，收集、觀察、比較、篩選有用的信息，抽象成數學問題。第二個轉化是根據已抽象出來的數學問題，分析其中的數量關系，探究解決問題的方法并求解，進而在實踐中檢驗，必要時還能反思自己解決問題的全過程。

在教學中，教師往往會重視第二個轉化，忽略第一個轉化，也就是我們所呈現的問題已經從實際問題中抽象出來，沒有無效信息和多余信息，指向性明確。而以上兩者轉化的能力在解決問題中是相輔相成、缺一不可的。本課在新課和練習環節中，創設了5個不同的生活情境，以期讓學生能在用方程解決問題中，嘗試進行這兩個轉化。并且讓學生在解決散步問題、挖隧道問題、購物問題、面積問題后（問題見下圖），與前面的行程問題進行回顧溝通。

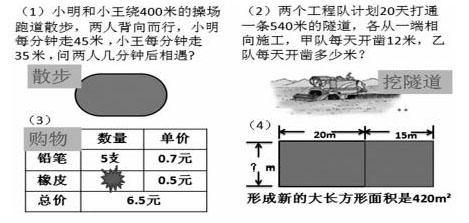
師：這些問題好像都不一樣，有沒有相同的地方？

生：用方程解決問題的步驟和方法是一樣的。

生：這幾個問題所列的等量關系都差不多。

師：既然說這5個問題都是相同的，那你能不能用一個含有字母的式子來表示我們今天學的所有的方程？

生：ax+bc=d。

即使購物問題中鉛筆和橡皮的數量不同，學生也能感受到這一系列問題內在的等量關系是一致的，都可以用一個含有字母的式子來表示。這能幫助學生找到這些題目之間的內在聯系，讓學生初步體會兩積之和逆解問題的基本模型，建立起解決這一類問題的數學模型。

總而言之，“回顧與反思”的意識和水平，在學生解決問題能力的培養上起著很大的作用，“回顧與反思”其實就是對于學生“元認知”的培養，教師要在解決問題教學中引導學生從不同的角度進行“回顧與反思”，從而提升解決問題的能力。

參考文獻：

[1]陳美潔.淺談小學數學解決問題中的回顧與反思[J].新課程（上），2018（5）.

[2]朱向明.在回顧與反思中提升數學思維——蘇教版教材“回顧與反思”的內容編排與教學建議[J].小學數學教育，2015（Z4）.

[3]張丹.“問題解決”目標的內涵及實現[J].江蘇教育，2014（11）.

[4]周玉仁.從“應用題”到“解決問題”[J].小學數學教師，2010（7-8）.

（浙江省杭州市東城第二實驗學校 ? 310020）