解析“雞兔同籠”問題中存在的“慣性假設思想”

范 敏

(安徽省銅陵市愛國小學 244000)

“雞兔同籠”問題是我國民間廣為流傳的數學趣題，最早出現在《孫子算經》中.是具備趣味性、挑戰性及培養學生思維能力、邏輯能力的典型題型.常見的解法有：列表法、假設法、圖示法、解方程法、金雞獨立法、抬腳法、砍腳法、安腳法、面積法.

案例呈現

例1雞兔同籠，有5個頭，14只腳，問雞、兔各幾只？

師：請同學們讀一讀，你從題里知道了幾個條件？分別是什么？籠子里有多少只雞和兔，我們一起來猜一猜好嗎？

師：如果遇到數目大的時候，這種方法行嗎？怎么辦呢？(過渡到假設法)

生：假設全是雞：

5×2=10(只)……如果把兔全當成雞一共就有10只腳.

14-10=4(只)……每只兔就少了2只腳，4只腳是少算了兔的腳數.

4-2=2(只)……1只兔當成1只雞就要少算2只腳.

4÷2=2(只) ……那把多少只兔當成雞算就會少4條腿呢？就看4里面有幾個2就是把幾只兔當成了雞來算，所以4÷2=2就是兔的只數.

師：除了假設全是雞還可以怎么假設？

生：假設全是兔……

在執教”雞兔同籠”問題時，老師們常常運用猜測和列表，初步感知發現形成規律，進而過渡到假設全是雞或兔的情況，在老師提出讓學生假設時，學生馬上能給出假設全是雞或兔的情況.筆者認為這是教師主觀的“慣性假設思想”.首先學生不了解什么是假設法，他可以怎樣假設，其次是不理解為什么選擇假設全部都是雞或兔.

策略呈現 例1雞兔同籠，有5個頭，14只腳，問雞、兔各幾只？

師：籠子里有多少只雞和兔，我們一起來猜一猜好嗎？

生1：可能有1只雞4只兔.

……

生5：可能有5只雞0只兔.

師：咱們可以將剛才猜測的不同情況列出表格.

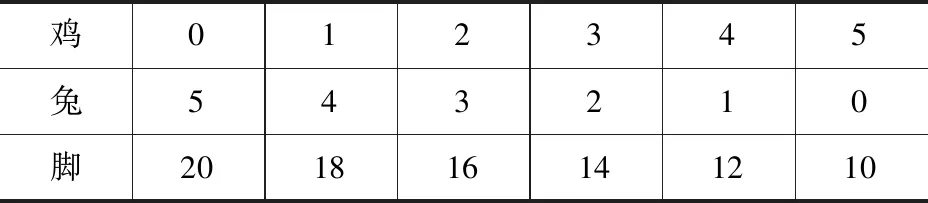
雞012345兔543210腳201816141210

師：你有什么發現么？誰猜對了？

生：我發現×××猜得很準確：3只雞2只兔剛好14只腳.

師：他是不是每次都能猜對呢？

生：不能每次都能猜到準確答案.

師：仔細觀察表格你還有什么發現嗎？

生1：我發現雞的只數越多總腳數就越少，反之兔的只數越總腳數就越多.

生2：雞和兔的總頭數都是不變的.

生3：從左往右看每增加一只雞，減少一只兔，總腳就減少2只.從右往左看每減少1只雞，增加1只兔，總腳數就增加2.

師：你的發現真了不起.根據你的發現前面猜錯的同學可以補救調整得出正確結果么？

生4：哦，我知道了.剛才我猜的是4只雞1只兔，總腳數比實際腳數少2只.那我就可通過減少1只雞，增加1只兔總腳數就會增加2.就能得出3只雞2只兔共14只腳.

師：能聽懂么？覺得他這種調整的思路怎么樣？

生5：我覺得非常好，這個方法我也會了.我剛才猜的是1只雞4只兔，總腳數多了4只.我可以增加2只雞，減少2只兔子.總腳數就減少4只.得出正確結果是：3只雞2只兔.

師：看來這個方法很不錯.你們能根據這種調整的思路列出算式么？

生1：假設1只雞，4只兔

2×1+4×4=18(只) 18-14=4(只) 4÷2=2(只)

1+2=3(只雞) 4-2=2(只兔)

生2：假設2只雞，3只兔

2×2+3×4=16(只) 16-14=2(只) 2÷2=1(只)

2+1=3(只雞) 3-1=2(只兔)

生3：假設4只雞，1只兔

2×4+4×1=12(只) 14-12=2(只) 2÷2=1(只)

4-1=3(只雞) 1+1=2(只兔)

生4：假設全是雞

2×5=10(只) 14-10=4(只)

4÷2=2(只兔) 5-2=3(只雞)

生5：假設全是兔

4×5=20(只) 20-14=6(只)

6÷2=3(只雞) 5-3=2(只兔)

師：比較一下這幾種不同的假設，你有什么發現么？

生1：這些都是沒有猜對答案，通過調整后得出結果的.

生2：我發現假設全是雞或兔的這2種情況在計算時更容易理解計算起來也更方便.……

蘇聯教育家贊可夫說過:凡是兒童自己能夠理解和感受的一切，都應當讓他們自己去理解和感受.

教師首先引導學生從列表法觀察發現蘊含的規律，讓學生在這一過程中體會到：根據表實際的總腳數與自己猜想的總腳數差，來調整數據，對假設法的探究起到了鋪墊作用，進而讓學生大膽嘗試采用各種可能性進行假設發現每一種可能性均可通過假設—計算—推理—解答得出正確結果.最后讓學生觀察對比不同假設方案進而得出假設都是雞或都是兔這兩種方案計算起來會更簡便算式也更容易理解，優化了解題策略.從引導認識到優化假設方案循序漸進，水到渠成.

雖然本節課研究的內容有些抽象，但這些抽象的東西其實都來源于現實生活.因此，真正的知識是來源于感性經驗的，我們的數學教學不能脫離學生的經驗，簡單枯燥的講解已經遠遠不能滿足現在學生的需要.所以數學課越來越注重加入動手操作、小組討論、合作學習等活動，希望通過活動讓學生獲得更多數學經驗.直接的活動經驗可以通過猜想、繪畫、交流探討中獲得，而間接的經驗可以在構建數學模型中所獲得，思考的活動經驗需要通過分析、歸納等方法獲得數學經驗，如預測結果、探究成因等等.