鋼彈簧損傷對地鐵列車-浮置板軌道振動性能的影響

魏新江， 史文超， 蔣吉清， 張佳斌， 丁 智

(1.浙江大學城市學院 工程學院，杭州 310015；2.安徽理工大學 土木建筑學院，安徽 淮南 232001)

鋼彈簧浮置板軌道在城市軌道交通中得到了廣泛應用[1]，相比其他軌道結構具有更優良的減振降噪作用[2-3]。浮置板軌道結構的原理是：在軌道和基礎間插入固有頻率遠低于激振頻率的線性諧振器，借以減小傳入基礎的振動，降低下部結構傳振和傳聲。國內外對于浮置板軌道的振動響應研究已相當成熟，王瀾等[4]基于MSC/DYTRAN軟件建立了浮置板軌道結構與列車耦合系統的有限元模型，對比分析了浮置板軌道與普通道床軌道的振動響應，對浮置板軌道的隔振效果進行了評價。李增光等[5]研究了浮置板軌道參數激勵振動的形成機理和影響因素，并提出了減少參數激勵振動的控制措施。Hussein等[6]對連續型浮置板軌道結構進行了研究，利用傅里葉變換得到計算得到簡諧荷載下的位移響應。

上述研究均針對完整軌道結構展開。然而，隨著軌道交通運營年限的增加，可能出現部分鋼彈簧隔振器失效等情況，由于鋼彈簧隔振器數量較多且浮置板自身剛度較大，因此，個別鋼彈簧隔振器失效一時很難被發現[7]。對浮置板軌道而言，隔振器是保障軌道結構減振降噪作用的關鍵，如果鋼彈簧受到損傷，將影響軌道系統剛度均勻性和完整性，甚至威脅地鐵列車的安全運營。因此，研究浮置板軌道鋼彈簧損傷對車軌振動性能的影響具有重要的意義。國內外學者對浮置板軌道結構損傷做了大量研究[8-12]，但現有研究大多關注扣件失效對軌道振動的影響，對于鋼彈簧損傷的研究相對較少。余關仁等采用等效輪軌作用力來模擬列車荷載，建立了浮置板軌道的ANSYS有限元模型，并分析了扣件和鋼彈簧結構在完全失效情況下的浮置板振動性能，包括鋼彈簧失效數量及失效位置對軌道系統振動性能的影響。本文建立了浮置板鋼彈簧損傷情況下的地鐵列車-浮置板軌道-襯砌-地基整體分析模型，基于理論分析和數值積分算法探討了鋼彈簧損傷數量、損傷程度、損傷位置、列車速度等因素對于車軌系統振動的影響，旨在為地鐵車軌的安全運營和后期維護提供參考。

1 車軌模型及平衡方程

1.1 車軌系統模型

根據車輛-軌道耦合動力學原理[13]，建立二維車軌系統模型。列車采用由一、二系懸掛的車體、轉向架及輪對組成的10自由度多剛體模型，其中，車體、轉向架考慮豎向平動及點頭兩個自由度，輪對僅考慮豎向平動。地鐵的兩根鋼軌視作整體，采用兩端簡支的Euler梁進行模擬；浮置板則采用兩端自由的Timoshenko梁模型，由于相鄰浮置板之間的空隙很小，在計算中近似取為0；基底墊層及襯砌視作整體，采用Timoshenko簡支梁進行模擬。鋼軌扣件和浮置板鋼彈簧均視為離散分布的彈簧阻尼系統，其中扣件分布間隔為0.625 m，鋼彈簧間隔為1.25 m；地基土體對地鐵隧道的影響采用均布彈簧阻尼模型近似模擬。為簡化起見，輪軌互相作用采用近似的線彈性接觸，且只考慮單節車廂作用，如圖1所示。

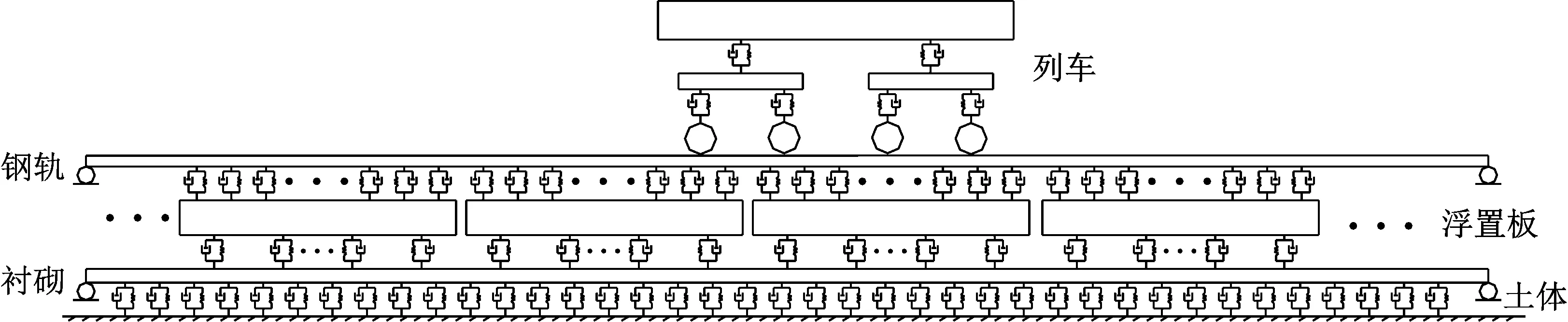
圖1 地鐵列車-軌道-襯砌-地基耦合模型

1.2 動力平衡方程

首先，依據達朗貝爾原理建立列車振動的微分方程，其矩陣表達式為

(1)

式中：Mv，Cv和Kv分別為車輛的質量矩陣、阻尼矩陣及剛度矩陣；yv為列車的豎向位移向量，上標“˙”、“˙˙”分別表示位移關于時間的一階、兩階導數；Fv為列車各部分所受外力，包括自重及豎向輪軌接觸力(兩根鋼軌之和)。

其次，建立鋼軌的振動方程。鋼軌采用兩端簡支的Euler梁進行模擬，其動力學方程為

(2)

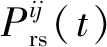
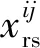
浮置板及襯砌均采用Timoshenko梁模型，動力控制方程如下

(3)

式中：κAG為修正剪切剛度；ρA為梁的分布質量；EI為梁的抗彎剛度；y(x,t)和φ(x,t)分別為梁的豎向位移和轉角；f(x,t)和T(x,t)分別為作用在梁上的豎向分布外力及分布彎矩。

基于模態疊加法的思路，可假設鋼軌豎向位移表達式為

(4)

式中：yrk(x)=sinkπx/lr為鋼軌第k階自振模態，lr為鋼軌長度；qrk(t)為鋼軌振動的廣義函數；mr為鋼軌模態階數。

同樣根據模態疊加法并結合動力控制方程式(3)，可得到浮置板豎向位移和轉角的模態表達式如下

(5)

式中：ms為浮置板模態階數；qsp(t)為浮置板振動的廣義函數；ysp(x)和φsp(x)分別為浮置板第p階豎向位移及轉角自振模態，具體形式可結合兩端自由的邊界條件求解得到。

襯砌豎向位移和轉角的模態表達式可類似表示為

(6)

式中：mh為襯砌模態階數；qhp(t)為襯砌振動的廣義函數；yhp(x)和φhp(x)分別為襯砌第p階豎向位移及轉角自振模態。

將鋼軌、浮置板和襯砌的位移表達式分別代入各自的結構動力學方程，經正交解耦后即可得鋼軌、浮置板和襯砌的第k階振動常微分方程。

2 鋼彈簧損傷模擬及數值計算方法

根據上文推導，聯立列車方程與鋼軌、浮置板、襯砌等軌道結構的模態常微分方程，即可得到列車-軌道-襯砌-地基耦合振動方程。

為考慮鋼彈簧損傷，引入損傷系數α表示損傷后的鋼彈簧剛度，即Ks=(1-α)Ksh，其中Ksh為完好時的鋼彈簧剛度。當α為0時，鋼彈簧沒有損傷，當α為1時，鋼彈簧完全失效。將損傷鋼彈簧剛度Ks代替方程中的Ksh，即可求解鋼彈簧損傷情況下的車軌振動，而列車-軌道-襯砌-地基耦合方程的形式保持不變。

需指出的是，軌道系統理論上具有無窮多階模態，但在實際數值計算中只能取前面有限階進行分析。對于車軌振動系統而言，中低階模態起主導作用，而高階模態影響較小。本文計算中，鋼軌和襯砌分別取前500階模態，浮置板取前20階模態，結合模態分析法和Newmark-β數值計算方法，并取計算步長為0.000 5 s，經數值驗證可得到相對穩定和精確的計算結果。

3 鋼彈簧損傷對車軌振動性能的影響

3.1 計算參數及損傷模型

鋼軌和襯砌長度取為325 m，單塊浮置板長25 m，在計算長度內，共有13塊浮置板。單塊浮置板上扣件數量為40個，扣件間隔為0.625 m；單塊板下鋼彈簧為20個，間隔為1.25 m。地鐵隧道參數取自杭州地鐵1號線，為圓形盾構隧道，管片外徑6.2 m，厚350 mm，管片采用C50混凝土澆筑，彈性模量為34.4 GPa，考慮到管片連接等影響，對地鐵隧道剛度進行折減，折減系數取為0.2[14]。地鐵車輛考慮B型列車，浮置板軌道采用常見參數組合，車軌系統的動力計算參數見表1。其中，地基彈簧系數和地基阻尼系數取值參考了杭州市某地鐵區段的地勘報告資料，輪軌接觸剛度由Hertz非線性接觸公式推導等效而得[15]。

為考慮初始振動的影響，列車的起始位置取為浮置板前80 m，但數值計算的初始時刻t=0取為列車第一輪對剛進入鋼軌(即x=0)的時刻。

圖2為地鐵車軌系統的局部模型圖。圖中所示為軌道計算長度內第6、7兩塊浮置板(距離鋼軌左端點125 m至175 m區段)，圖中數字為浮置板下的鋼彈簧編號。下文的鋼彈簧損傷分析中，以該數字編號表示損傷鋼彈簧的位置。考慮到浮置板軌道的周期性變化，鋼彈簧損傷主要探討板端損傷和板中損傷兩種形式。

3.2 鋼彈簧損傷數量對車軌振動的影響

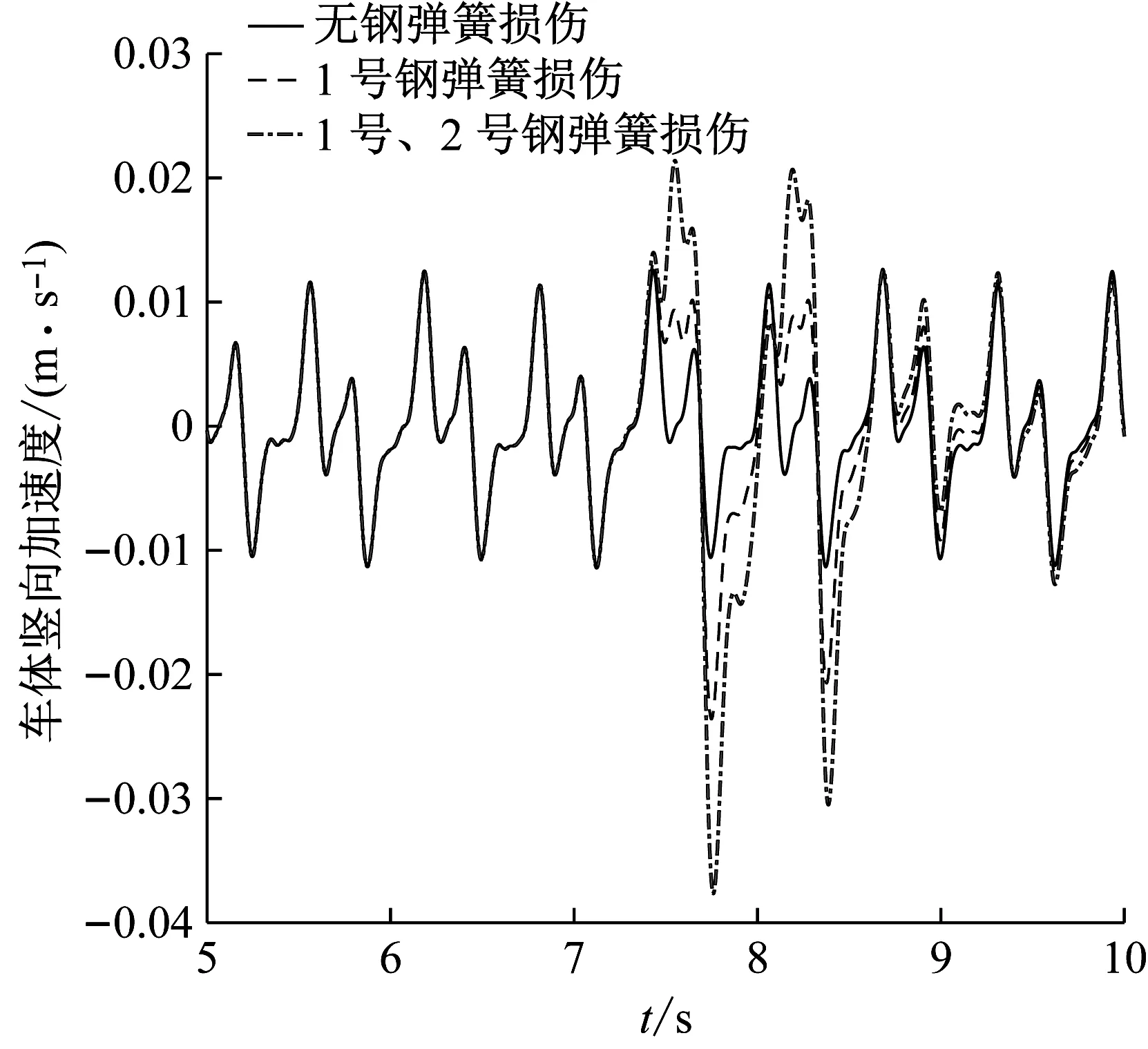
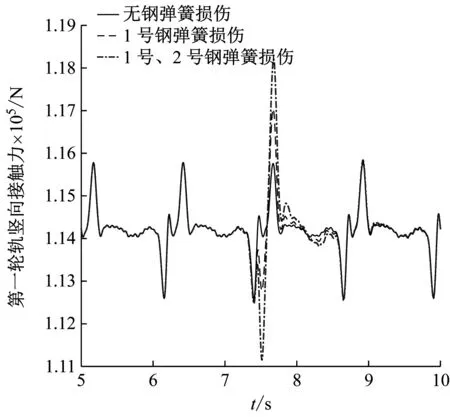
為研究鋼彈簧損傷數量對車軌系統振動性能的影響，分別探討無鋼彈簧損傷、1號鋼彈簧損傷、1號和2號兩個鋼彈簧損傷等三種工況下的車軌振動性能。損傷系數α取為0.9，當列車速度為72 km/h時，車軌系統的振動時程曲線如圖3所示。

由圖3可知，當列車到達鋼彈簧損傷區域附近時，車軌系統的各項動力響應都不同程度地增大。當t=7.5 s時，列車第一輪對剛好到達第7塊浮置板板端，即1號損傷鋼彈簧上方區域附近，此時，車軌系統豎向的車體加速度、輪軌接觸力、輪下鋼軌位移、襯砌中點加速度等振動響應增幅顯著。從影響范圍來看，車體豎向加速度、襯砌豎向加速度受鋼彈簧損傷的影響范圍較大，而豎向輪軌接觸力和輪下鋼軌豎向位移只在損傷鋼彈簧附近有振動變化。

表1 車軌系統計算參數

圖2 鋼彈簧損傷區域的車軌系統局部模型圖

(a) 車體豎向加速度

(b) 首對輪軌的豎向接觸力

(c) 輪下鋼軌豎向位移

(d) 襯砌中點豎向加速度

圖3 不同鋼彈簧損傷數量下的車軌振動時程曲線

Fig.3 Dynamic curves of train-track system under different number of damaged steel springs

此外，由圖3(a)可知，隨著鋼彈簧損傷數量的增加車體豎向加速度幅值也隨之增加，2個鋼彈簧損傷較無鋼彈簧損傷情況車體加速度幅值增加了2.3倍。我國國家標準GB 5599—1985關于乘車舒適性評判標準是以Sperling舒適度指標為基礎制定的，車體加速度越大，乘車舒適性越差，由此可知當列車經過有鋼彈簧損傷位置時，乘車舒適性和平穩性將受顯著影響。

輪對豎向接觸力也隨著鋼彈簧損傷數量的增加而增大，較大的輪軌接觸力會增加踏面的磨耗，加大鋼軌表面的損傷，對鋼軌使用壽命和維護產生不利影響。此外，根據圖3(c)和3(d)，在1號和2號鋼彈簧同時損傷情況下，輪下鋼軌豎向位移較完好工況增加了40%，而襯砌中點豎向加速度幅值相應增大了1.13倍。襯砌振動會影響周邊土體乃至鄰近建筑的振動，綜上可見，鋼彈簧損傷對地鐵系統的運營維護及周邊環境振動都將產生不利影響，應注意及時排查和更換損傷的鋼彈簧。

3.3 鋼彈簧損傷程度對車軌振動的影響

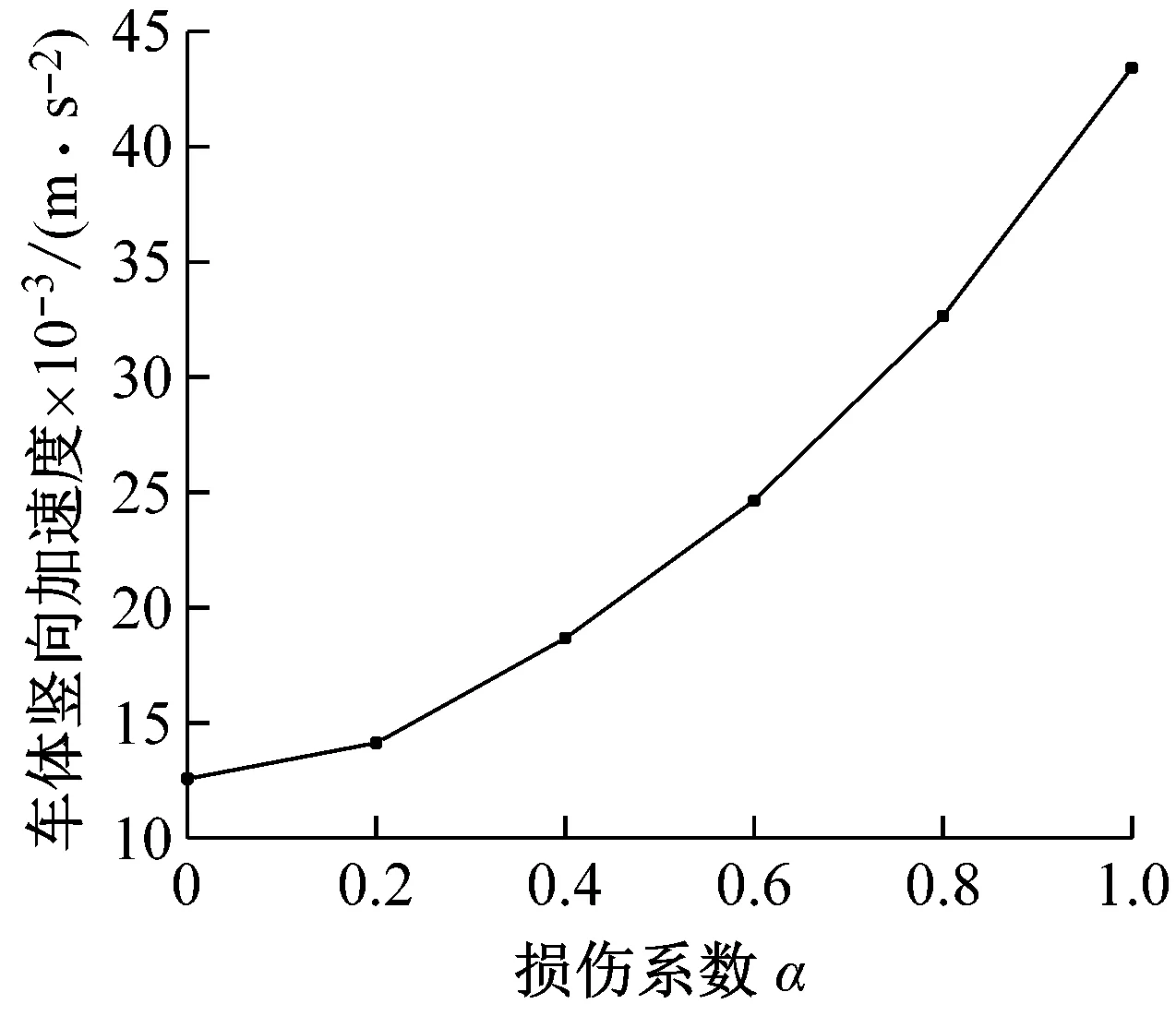
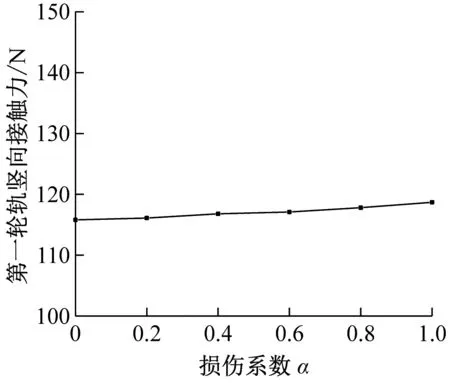
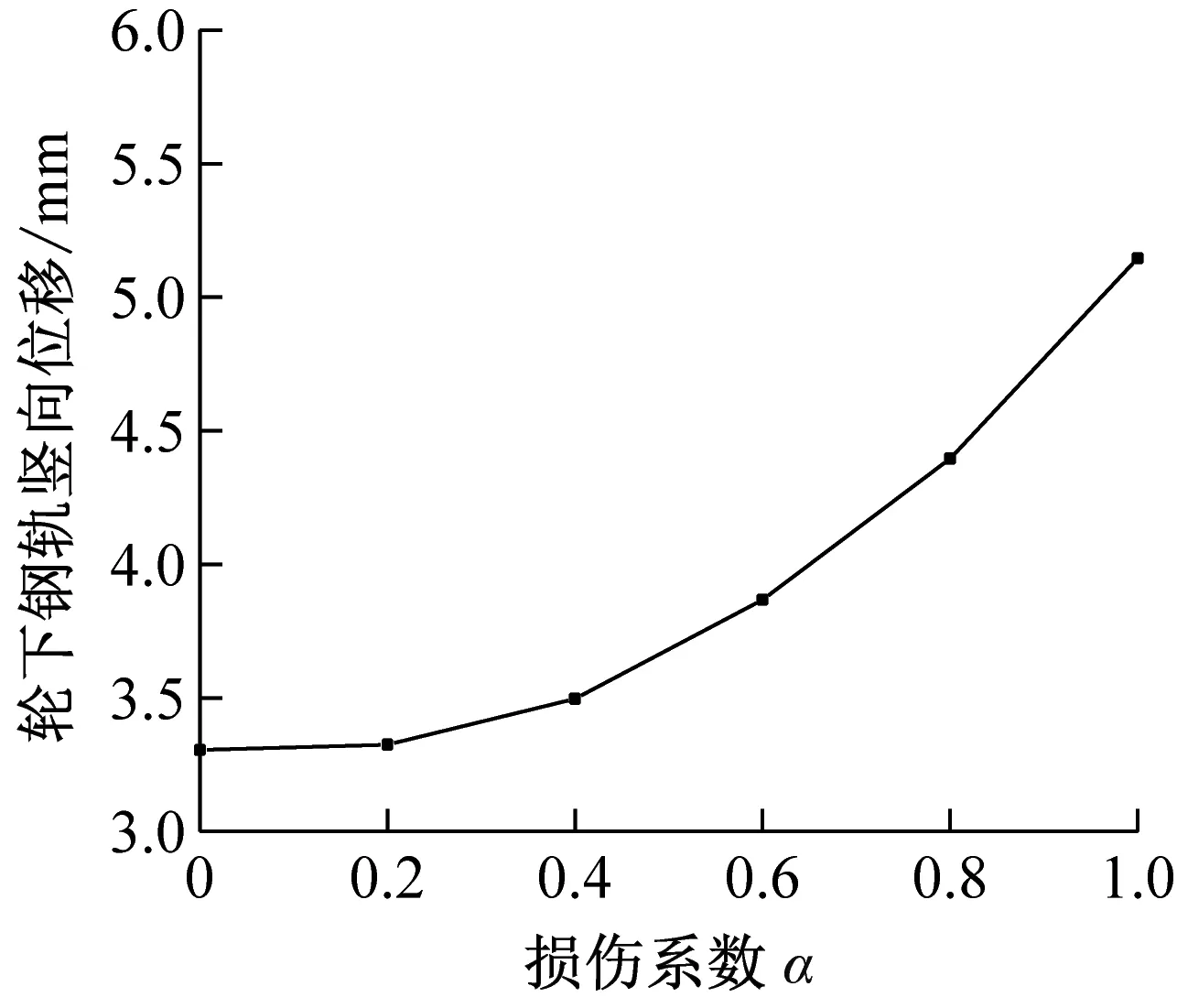
考慮1號和2號鋼彈簧同時損傷的情況，在不同鋼彈簧損傷程度下車軌系統的振動響應如圖4所示，列車速度仍取為72 km/h。

(a) 車體豎向加速度

(b) 首對輪軌的豎向接觸力

(c) 輪下鋼軌豎向位移

(d) 輪下浮置板豎向位移

(e) 軌中豎向加速度

(f) 襯砌中點豎向加速度

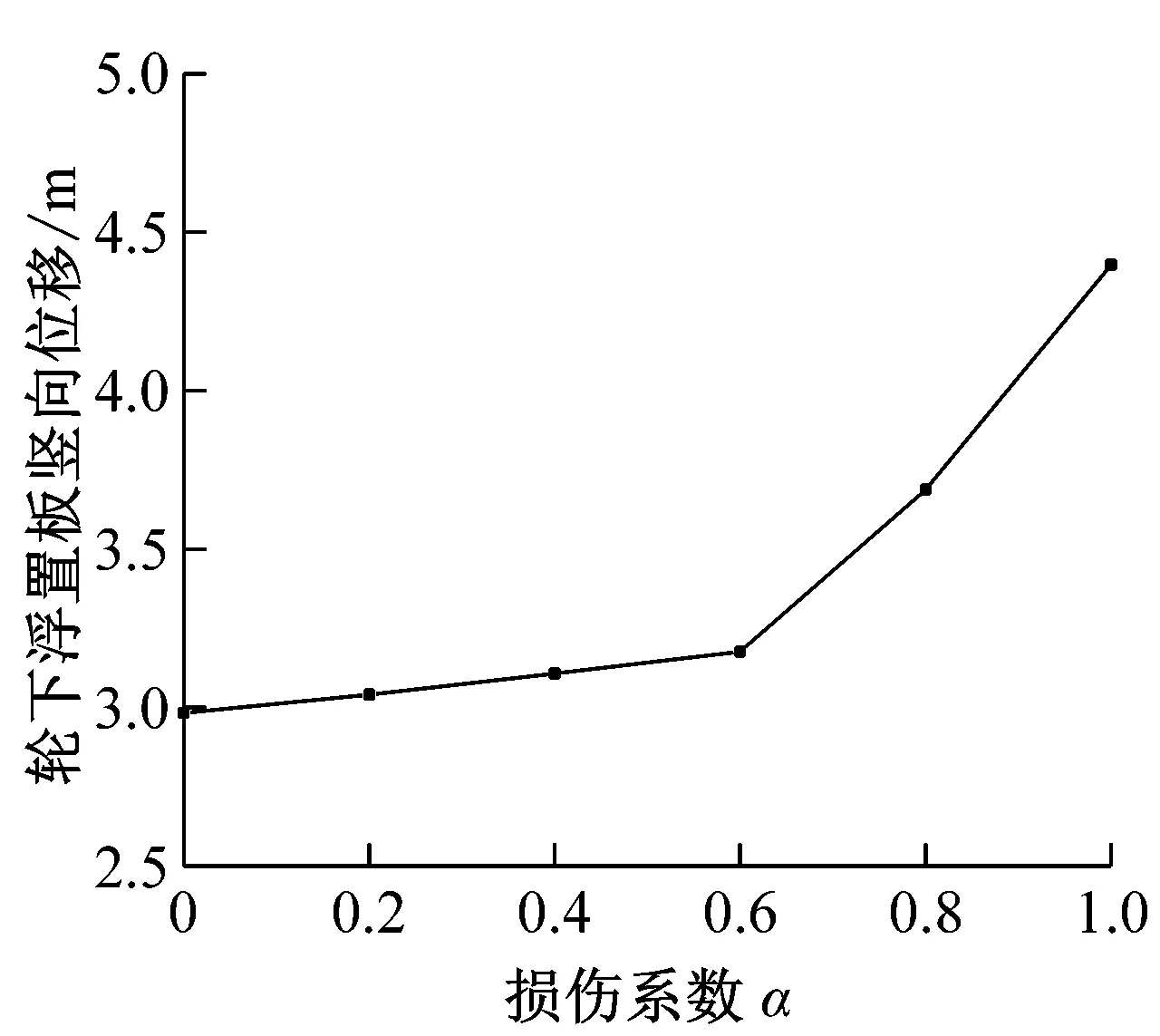
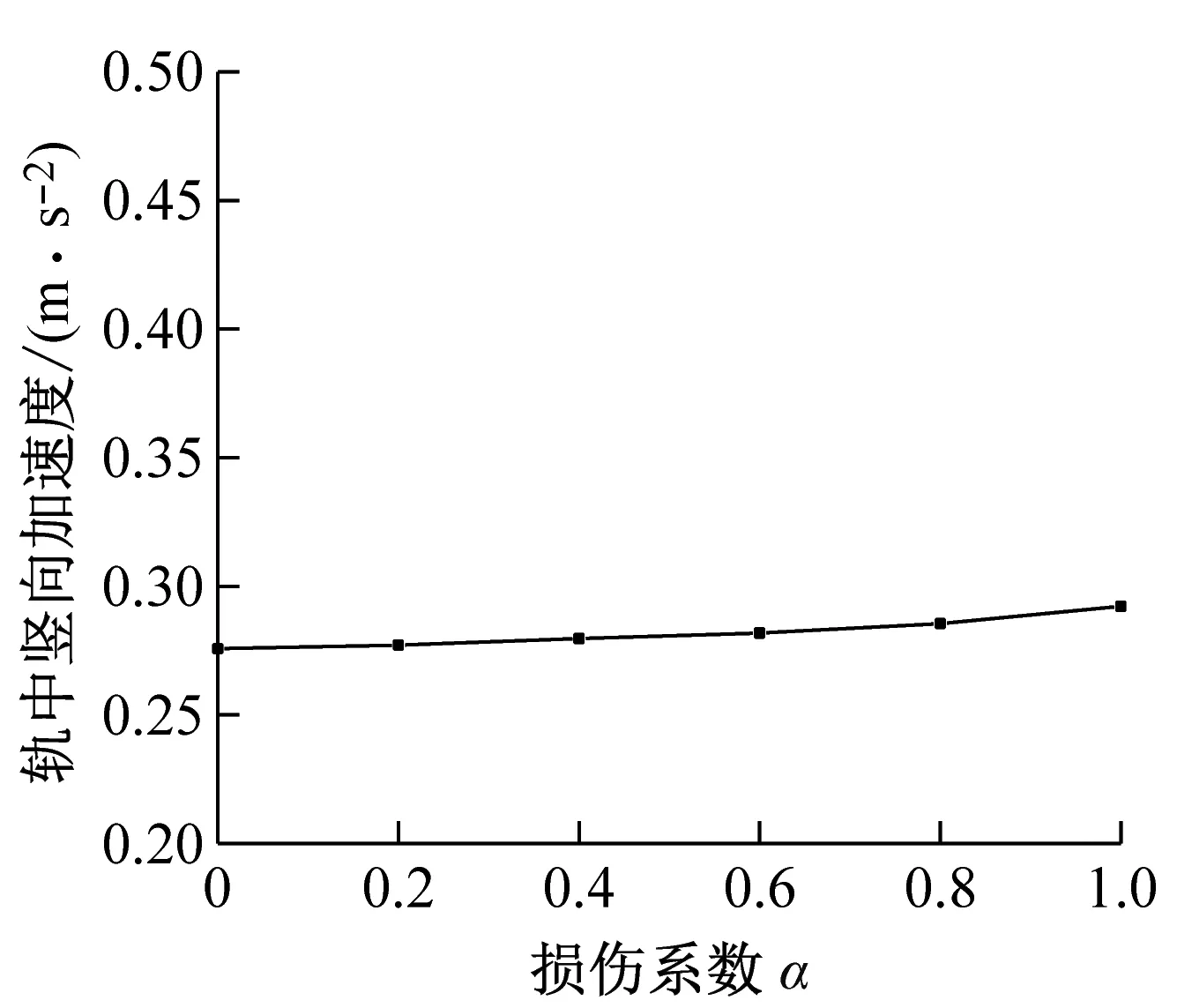
圖4 車軌振動幅值隨鋼彈簧損傷系數的變化曲線

Fig.4 Dynamic curves of train-track system versus damage coefficient of steel springs

由圖4可知，隨著鋼彈簧損傷系數α的增加，各項車軌振動均呈現增大的趨勢，其中車體豎向加速度、輪下鋼軌豎向位移、輪下浮置板豎向位移和襯砌中點豎向加速度增幅顯著，且變化曲線呈現越來越陡的趨勢。其中，隨著損傷系數α由0變化到1，車體豎向加速度增大了2.46倍，襯砌中點豎向加速度增大了1.4倍。

3.4 鋼彈簧損傷位置對車軌振動的影響

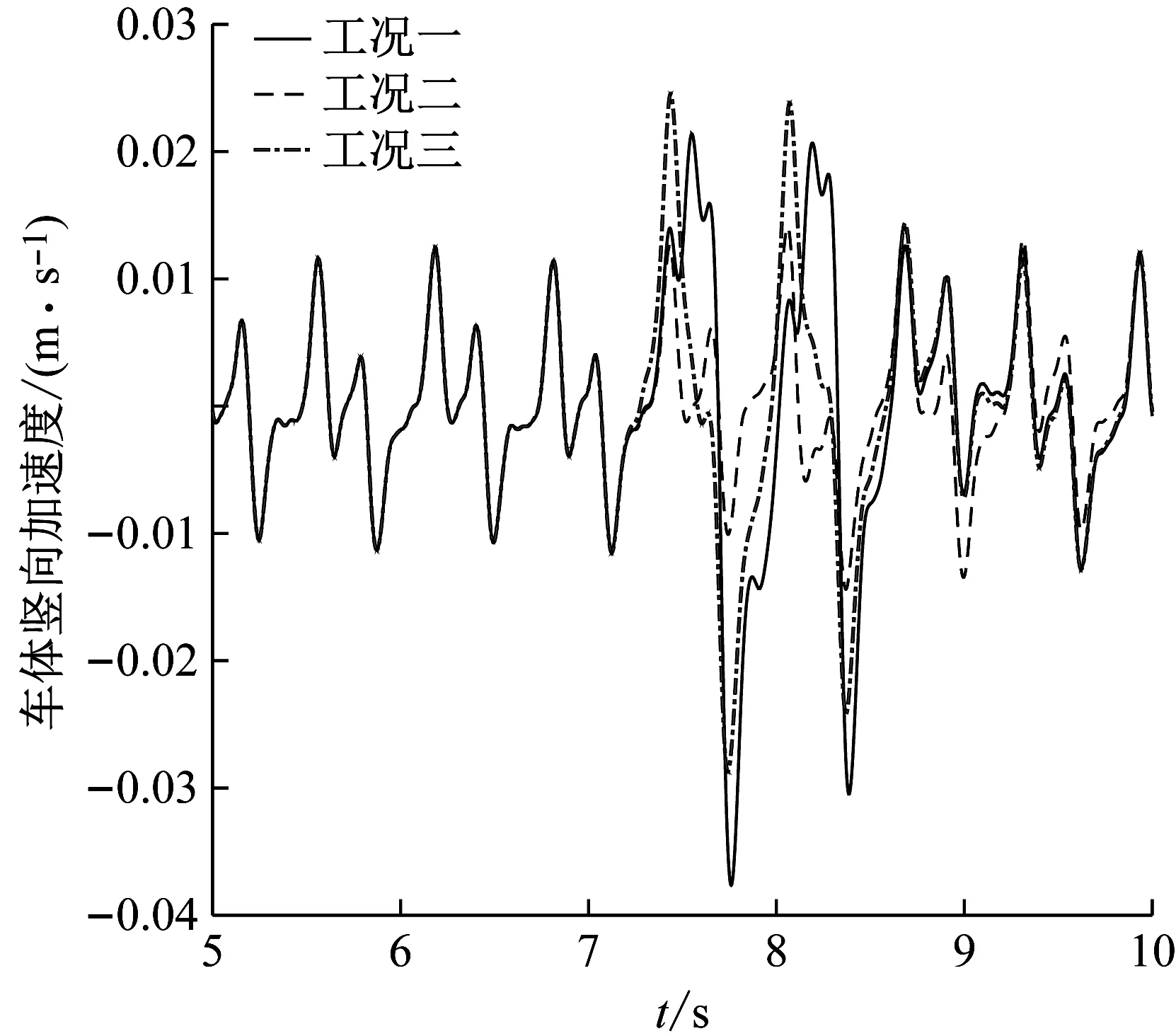
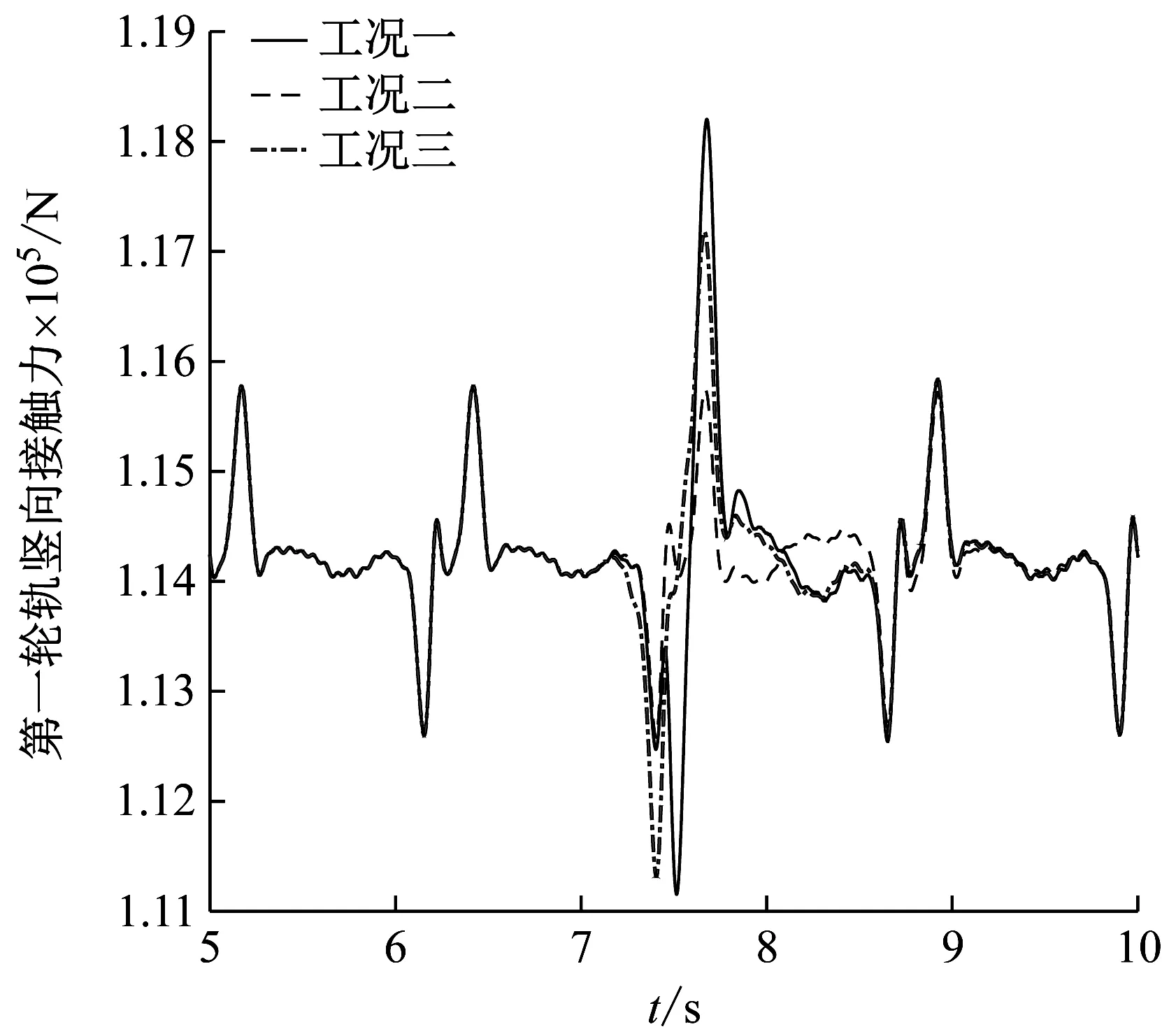
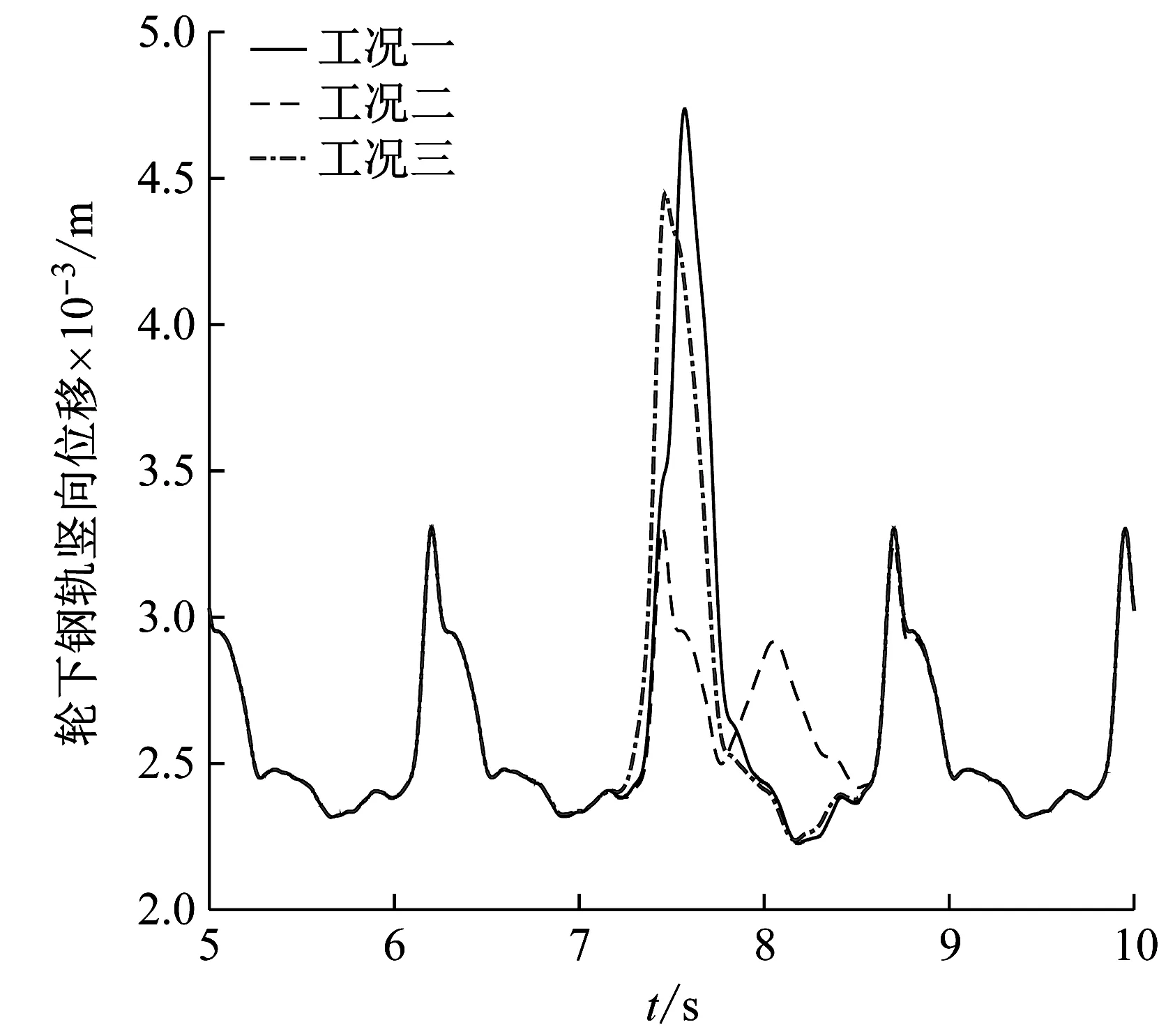
為研究鋼彈簧損傷位置對車軌振動性能的影響，將圖2的鋼彈簧損傷分為以下三種工況，工況一：1號和2號鋼彈簧損傷(同一塊浮置板的板端)，工況二：10號和11號鋼彈簧損傷(浮置板板中)，工況三：1號和-1號剛彈簧損傷(相鄰浮置板的板端)。鋼彈簧損傷系數α統一取為0.9。圖5所示為72 km/h列車速度下對應于三種工況的車軌系統動力響應時程曲線。

由圖5可知，鋼彈簧損傷位置對不同類型的車軌振動響應影響不同。在相同鋼彈簧損傷數量情況下，鋼彈簧損傷發生在浮置板中間時，對車軌各項振動響應的影響很小，而當損傷位置處于同一塊浮置板板端時，對各項振動指標的影響最大。對車體豎向加速度而言，工況一較無損傷情況增大了2.3倍；對于輪下鋼軌豎向位移，工況一較無損傷鋼軌位移增大了43.5%。由此可以得出，對于浮置板板端鋼彈簧的質量我們要更加關注，其狀態的好壞對車軌振動性能的影響較大，應及時檢查和維修，避免造成車軌系統的進一步損傷。

(a) 車體豎向加速度

(b) 首對輪軌的豎向接觸力

(c) 輪下鋼軌豎向位移

(d) 襯砌中點豎向加速度

圖5 三種工況下車軌系統的振動時程曲線

Fig.5 Dynamic curves of train-track system under three working conditions

3.5 鋼彈簧失效時列車速度對車軌振動的影響

圖6所示為在1號和2號鋼彈簧失效時，列車速度變化對車軌各項動力響應的影響。

(a) 車體豎向加速度

(b) 首對輪軌的豎向接觸力

(c) 輪下鋼軌豎向位移

(d) 襯砌豎向加速度

圖6 鋼彈簧損傷情況下列車速度對車軌系統振幅的影響

Fig.6 Influence of vehicle speed on vibration amplitudes of train-track system with damaged steel springs

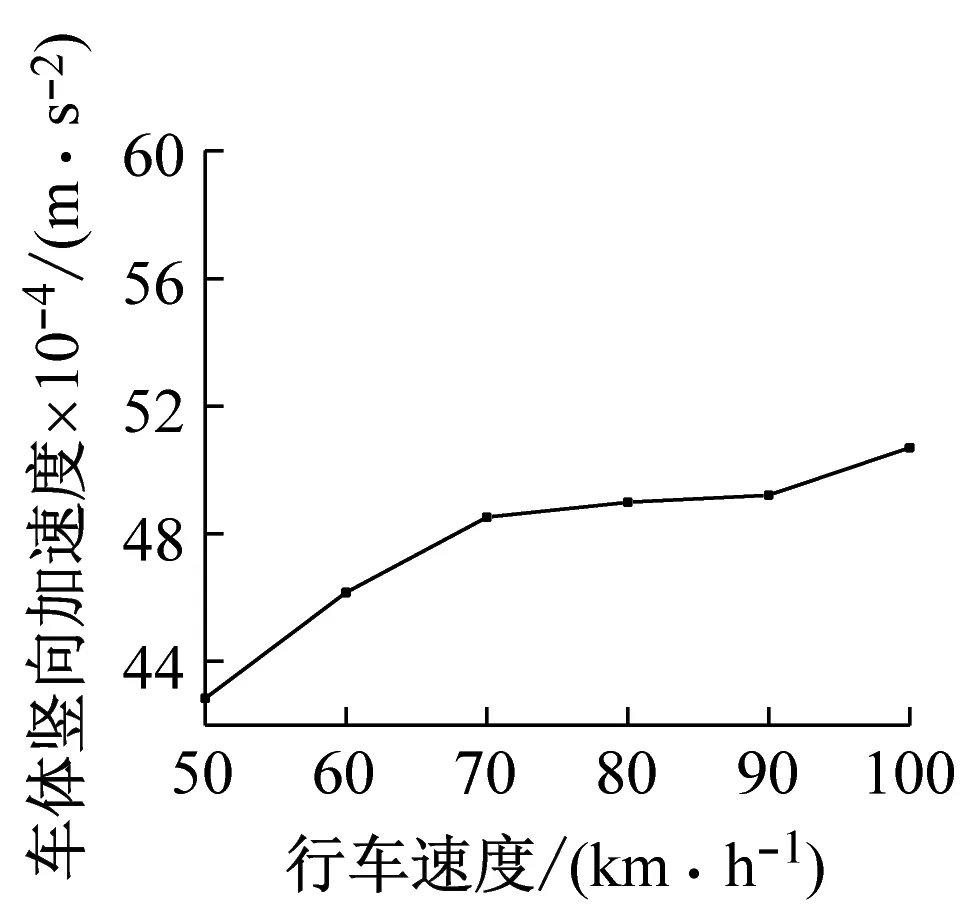
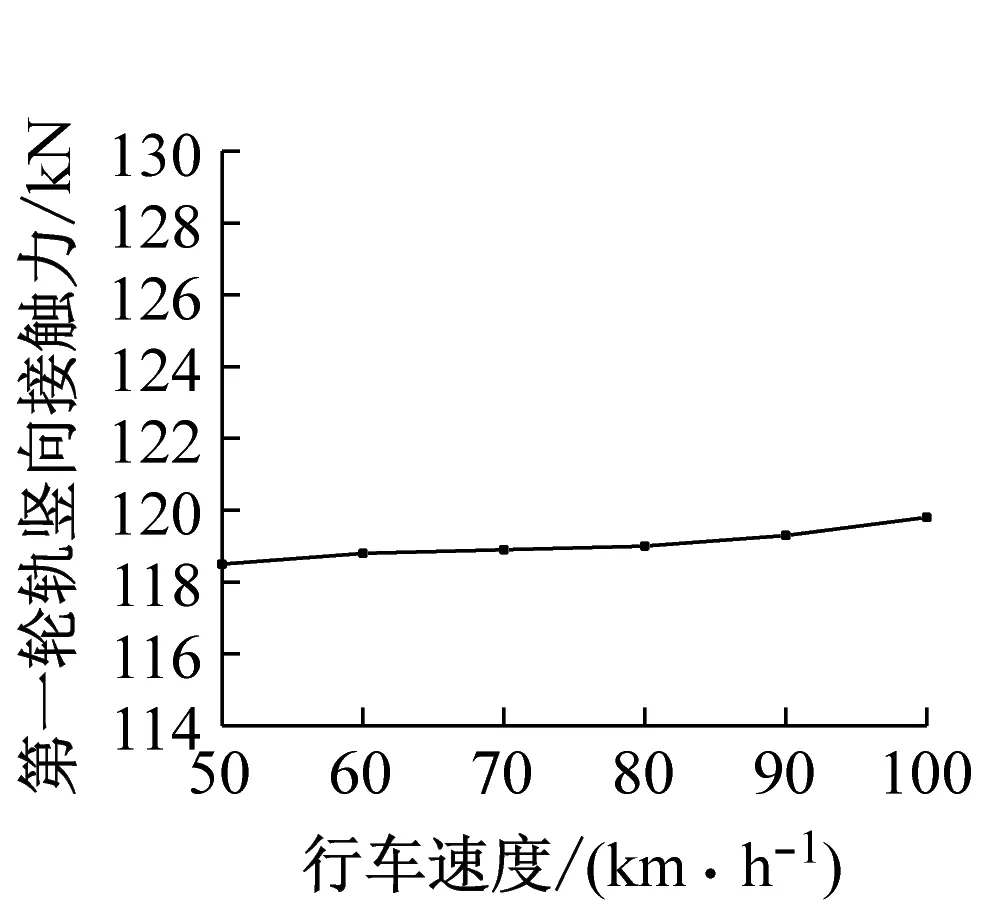
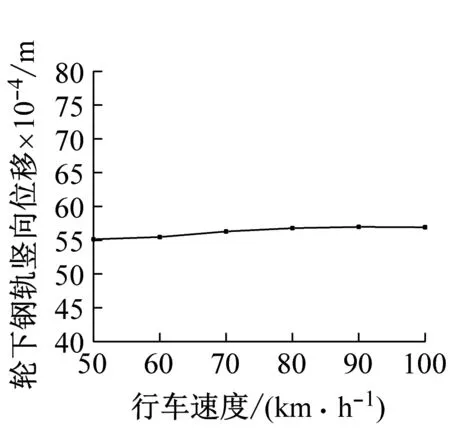
由圖6可知，在鋼彈簧損傷情況下，列車速度變化對車體豎向加速度、襯砌豎向加速度影響較大，豎向輪軌接觸力和輪下豎向鋼軌位移則基本不受影響。當列車速度由50 km/h增加到100 km/h時，車體加速度增加了18.3%，襯砌加速度增加了4.46倍。由此可知，列車速度的變化對鋼彈簧損傷情況下的乘車舒適性和周邊環境振動有較大影響，尤其是后者，應格外重視。

4 結 論

(1) 由于地鐵浮置板軌道的鋼彈簧剛度損傷導致軌道系統結構剛度不平順，加強了車軌系統的相互作用，對豎向的車體加速度、輪下鋼軌位移、輪軌接觸力、襯砌中心加速度都將產生重要影響，且振動幅值隨著鋼彈簧損傷數量的增加而增大。

(2) 鋼彈簧損傷程度對車軌系統的各項動力響應影響顯著，隨著損傷程度的增加各項振動幅值均持續增大，尤其是車體豎向加速度、輪下鋼軌豎向位移、襯砌中點豎向加速度等。

(3) 在相同鋼彈簧損傷數量情況下，損傷發生在同一塊板板端對車軌振動影響最大，損傷發生在浮置板中間時對車軌系統幾乎沒有影響。

(4) 在鋼彈簧損傷情況下，車軌各項振動均隨列車速度的增大而增大，其中車體豎向加速度和襯砌豎向加速度的增幅最為顯著。

總結而言，本文基于結構動力學理論和二維模型探討了浮置板鋼彈簧失效對車軌振動性能的主要影響和一般規律，通過分析發現車體豎向加速度和襯砌豎向加速度對鋼彈簧損傷最為敏感，可利用這兩項振動指標及時排查損傷，避免對地鐵乘車舒適性、周邊環境振動造成進一步不利影響，為地鐵長期運營維護服務。考慮到地鐵車軌系統的復雜性及浮置板單側鋼彈簧失效等情況，后續可建立更加精確的地鐵車軌三維空間模型，并考慮軌道不平順等影響，以進一步改進現有的研究工作。