一種基于極值-留數的高背景噪聲測試信號降噪方法研究

李 穎， 盧洪超， 周 琳， 陳文文， 齊聰山， 劉福順

(1. 浙江科技學院 中德工程師學院， 杭州 310023； 2. 中國海洋大學 工程學院， 青島 266100；3. 海洋石油工程(青島)有限公司， 山東 青島 266520)

對結構實測振動響應信號進行分析是獲取結構動力特性的重要手段。然而，在土木工程、海洋工程領域，測試設備、環境等因素導致測試的結構振動信號中不可避免的包含各種噪聲。信號中的噪聲不僅使結構模態識別的精度降低，還會產生“噪聲模態”[1]。當實測信號中包含可能淹沒結構固有模態的高背景噪聲時，結構模態參數識別十分困難。為此，在對工程結構進行模態參數識別、結構損傷診斷和健康檢測時，為了保證分析結果的正確性，往往需要采取合理的技術手段降低測試噪聲的影響[2]。

目前，已經有許多信號消噪技術應用于工程實踐。Cadzow[3]提出了基于奇異值分解(Singular Value Decomposition, SVD)的低秩逼近算法，該方法運用結構響應數據構建Hankel矩陣，進行SVD分解，認為較小的奇異值對應噪聲，將其置為零并重構Hankel矩陣，從而達到消噪的目的。該方法對信噪比(Signal-Noise Ratio, SNR)較小的信號消噪效果較好，當噪聲能量較大時，噪聲成分對應的奇異值可能比結構固有成分對應的奇異值更大，從而表現出消噪局限性；另外，當響應數據較大時，導致Hankel矩陣的維數較大，進行SVD分解會消耗大量計算機資源[4]，甚至無法完成計算。Shumway等[5]對時域平均法作了詳細闡述，時域平均法用一段數據的平均值代替中心點的數值，進行平均的方式包括直接平均、多項式平均和周期回歸平均等方法，并將各種方法應用于時間序列，對時間序列進行光滑。時域平均法具有一定的消噪效果，但各種平均方法的選取缺乏參照，沒有對消噪效果進行定量討論，另外運用該方法還需要時標信息，而且要有足夠的數據量。Kim等[6]在頻域內對頻響函數(Frequency Response Function, FRF)運用小波分解進行消噪，并將該方法運用于2自由度質量-彈簧-阻尼系統，能夠有效消除信號中添加的高斯白噪聲，但小波消噪算法對小波核函數的選擇有較大依賴性，在實際運用中受到一定局限。Wu等[7-8]對經驗模態分解(Empirical Mode Decompositon, EMD)的研究表明，白噪聲經EMD分解得到的固有模態函數(Intrinsic Mode Function, IMF)分量的統計特征滿足正態分布，IMF的能量密度與對應的平均周期的積為常量，這些研究結果為EMD消噪提供了理論基礎。對含噪聲的信號進行EMD分解，得到頻率從高到低的IMF，高頻部分受噪聲影響較大，低頻部分受噪聲影響較小，而信號的能量也主要集中在低頻段，使用低頻段的IMF進行重構完成消噪過程[9]。基于EMD分解的消噪方法對模擬的高信噪比信號具有較好的消噪效果，但該方法可能舍棄部分有用信號的能量，而且無法準確判定選取有效IMF的個數。另外，近年來還有學者運用EMD分解方法對非平穩信號的消噪進行消噪研究，并應用于轉子振動信號的去噪，取得了較好效果[10]。

本文將從信號分解的角度出發，提出一種基于極值-留數的信號分解消噪方法，該方法提取代表信號中固有信息的極值和留數，并根據這些信息進行重構，從而達到消噪目的。與傳統方法相比，本文方法避免反復進行SVD分解運算，具有較高的計算效率。另外，進行信號分解時，無需積分變換的核函數，便于實施。該方法能夠解決實際工程中在遭遇高背景噪聲時，其結構固有信息往往被當做環境噪聲而剔除的問題。文中將首先應用一質量-彈簧-阻尼模型進行驗證，然后應用實測海洋平臺加速度響應數據進一步研究新方法在實際工程中的應用效果。

1 信號分解方式

1.1 傅里葉序列

連續函數y(t)的周期為T，其傅里葉分解為

(1)

(2)

對于實測的離散數字信號yk(k=0,2,…,N-1)，其傅里葉分解為

(3)

其中xn=ei(2πn/N)。

1.2 Prony序列

連續信號y(t)分解成復指數的形式為[11]

(4)

式中:p為分解階次;λn為極值，由于y(t)為實數，λn必須為實數或為共軛復數對。令λn≡-αn+iωn，αn為阻尼系數，ωn為角頻率。系數γn為留數，它與λn成對出現，或為實數，或為共軛復數。令γn≡Aneiθn，其中An為各個成分的幅值，θn為對應相位。

等間隔采樣離散信號yk，其復指數分解為

(5)

式中:zn=eλnΔt。

2 基于極值-留數的信號降噪方法

對信號進行Prony分解，得到一系列極值和留數，每個極值和對應的留數表示信號中的一個成分。通過式(4)進行疊加，即可用極值和留數表示實測信號。當信號中包含噪聲成分時，噪聲成分也有對應的極值和留數，本文方法就是通過剔除噪聲成分的極值和留數，從而達到消噪的目的。因此本文消噪方法的關鍵在于準確求解信號所對應的極值和留數。

為了求解式(4)中的極值和留數，引入高階微分方程

(6)

(7)

式(4)為式(6)的通解，其中λn為式(6)對應特征方程式(7)的根。

對于實測的等間隔采樣離散數據yk(k=0,1,…,N-1)，式(6)高階微分方程變為差分方程

(8)

式中:bn為常系數。令bn=1，式(9)對應的特征方程為

(9)

通過以下步驟求解極值和留數

步驟1將式(8)寫成矩陣形式，由于Y和y′已知，可求出向量b，即系數bk(k=0,1,…,p-1)

Yb=-y′

(10)

其中

(11)

(12)

(13)

步驟2將bk代入式(9)中，求得特征值zk(k=1,2,…,p)

步驟3將特征值zk代入式(5)中，即可求得對應的留數γk。

2.1 一階差分方程求解方法

由于求解方程式(10)時，存在病態問題，很小的誤差會使結果產生較大的偏差。為了解決病態問題，本文將高階差分方程轉化為一階差分方程，即令

x1,k=yk,x2,k=yk+1,…,xp,k=yk+p-1

(14)

則

(15)

式(8)可以寫成

xk+1=Fxk

(16)

其中

(17)

式(16)表明，其特征值即是方程式(7)的根。故可由響應數據yk構建Hankel矩陣

(18)

式中:ξ、η分別為Hankel矩陣的行數和列數，為了提高計算效率，ξ和η的值都取最接近于數據序列長度一半的整數。當k分別取0和1時，對H(0)進行奇異值分解，得

(19)

(20)

由式(21)得到系統矩陣A

(21)

對A進行特征值分析，得到特征值zn，則響應信號的極值λn=ln(zn)/Δt，將λn代入式(5)即可求得對應的留數γn。

2.2 噪聲信號分離與剔除

海洋結構實測振動數據y(n)可以看作由兩部分組成[12]

y(n)=yreal(n)+ynoise(n)

(22)

式中:yreal(n)為結構的真實響應信號;ynoise(n)為實測信號中的噪聲信號。

對實測信號進行極值-留數分解，得到極值和留數

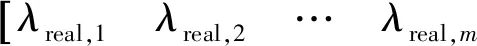
(23)

(24)

去除噪聲對應的極值和留數后，得到實真響應信號的極值和留數

(25)

(26)

根據式(5)重構響應信號，得到真實信號

(27)

極值-留數分解消噪算法步驟如下：

步驟1對海洋結構實測振動信號y(n)進行傅里葉變換，得到響應信號的頻譜；

步驟2根據頻譜找到峰值對應的頻率，并以此頻率為中心頻率設置頻率窗口；

步驟3對實測信號y(n)進行極值-留數分解，取極值的絕對值，將復頻率轉化為實頻率，選出步驟二頻率窗口中的實頻率對應的極值和留數；

步驟4通過式(5)，將步驟三得到極值和留數重構成時域信號，完成消噪過程。

3 數值算例

為了驗證本文方法的有效性，構建一個6自由度質量-彈簧-阻尼模型，如圖1所示。系統中各質量塊的質量為mi=100 kg，剛度為ki=5×107N/m，阻尼系數為ci=50 N·s/m，各質量塊的位移分別為xi，其中i=1,2,…,6。

圖1 6自由度質量-彈簧-阻尼模型

根據上述模型的系統狀態空間方程，利用MATLAB軟件的impulse函數生成離散脈沖響應數據。脈沖響應的采樣頻率設為500 Hz，信號序列包含2 048個點。對于不同的激勵點，整個6自由度系統會產生36個響應序列，為了便于分析，選取在質量m1處輸入、m1處輸出的脈沖響應數據進行研究，其時程如圖2所示。

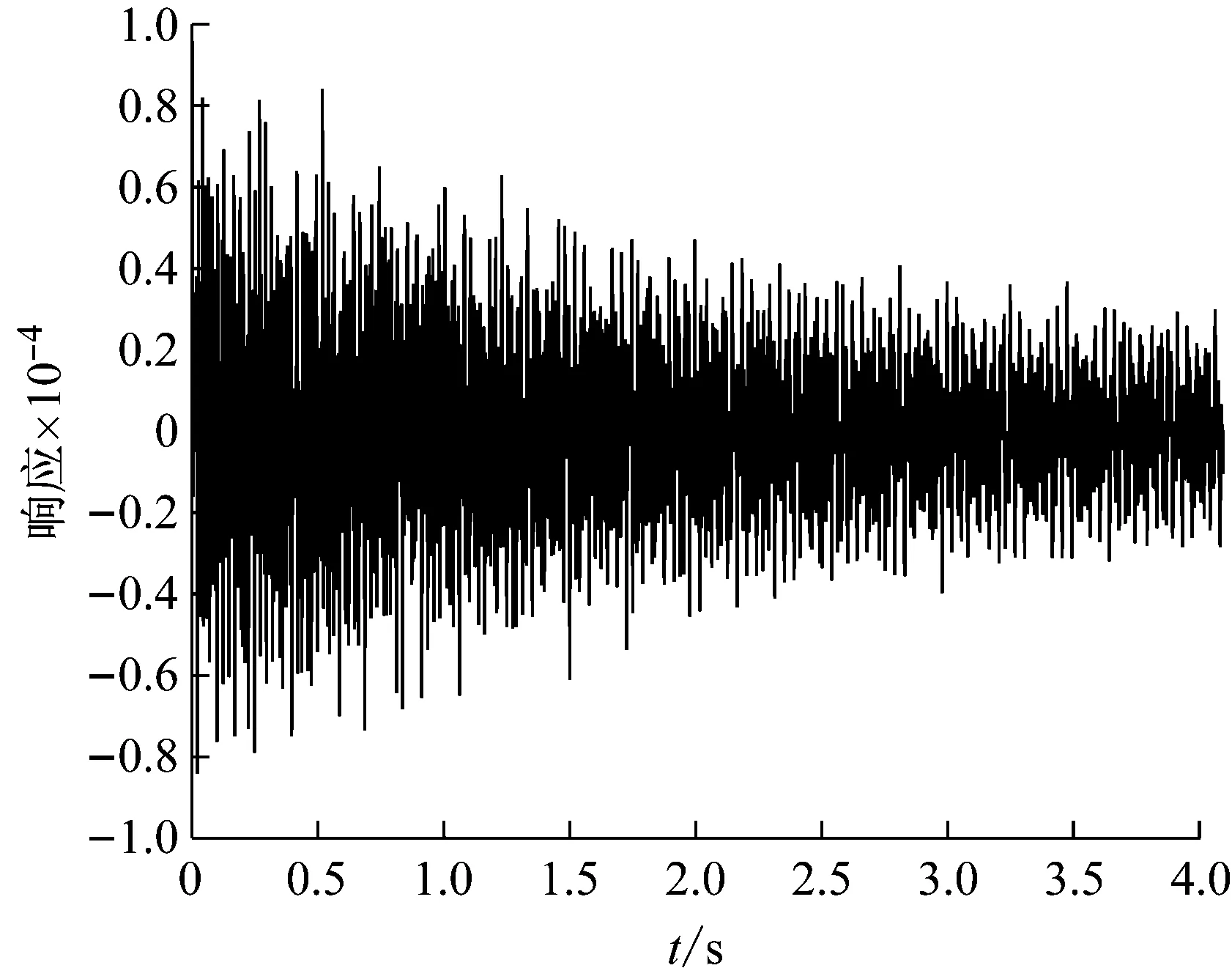
圖2 分析數據的時程圖

為了研究消噪效果，在信號中添加白噪聲模擬實測信號中的噪聲。使用SNR來描述噪聲水平，SNR為信號功率Ps與噪聲功率Pn之比，即SNR=10lg(Ps/Pn)。對分析數據分別添加不同信噪比的白噪聲，模擬實測信號中的不同強度噪聲。

對含信噪比為40 dB噪聲的信號和不含噪聲的信號進行傅里葉分析，得到信號的頻譜，它們的時程和頻譜對比如圖3所示。

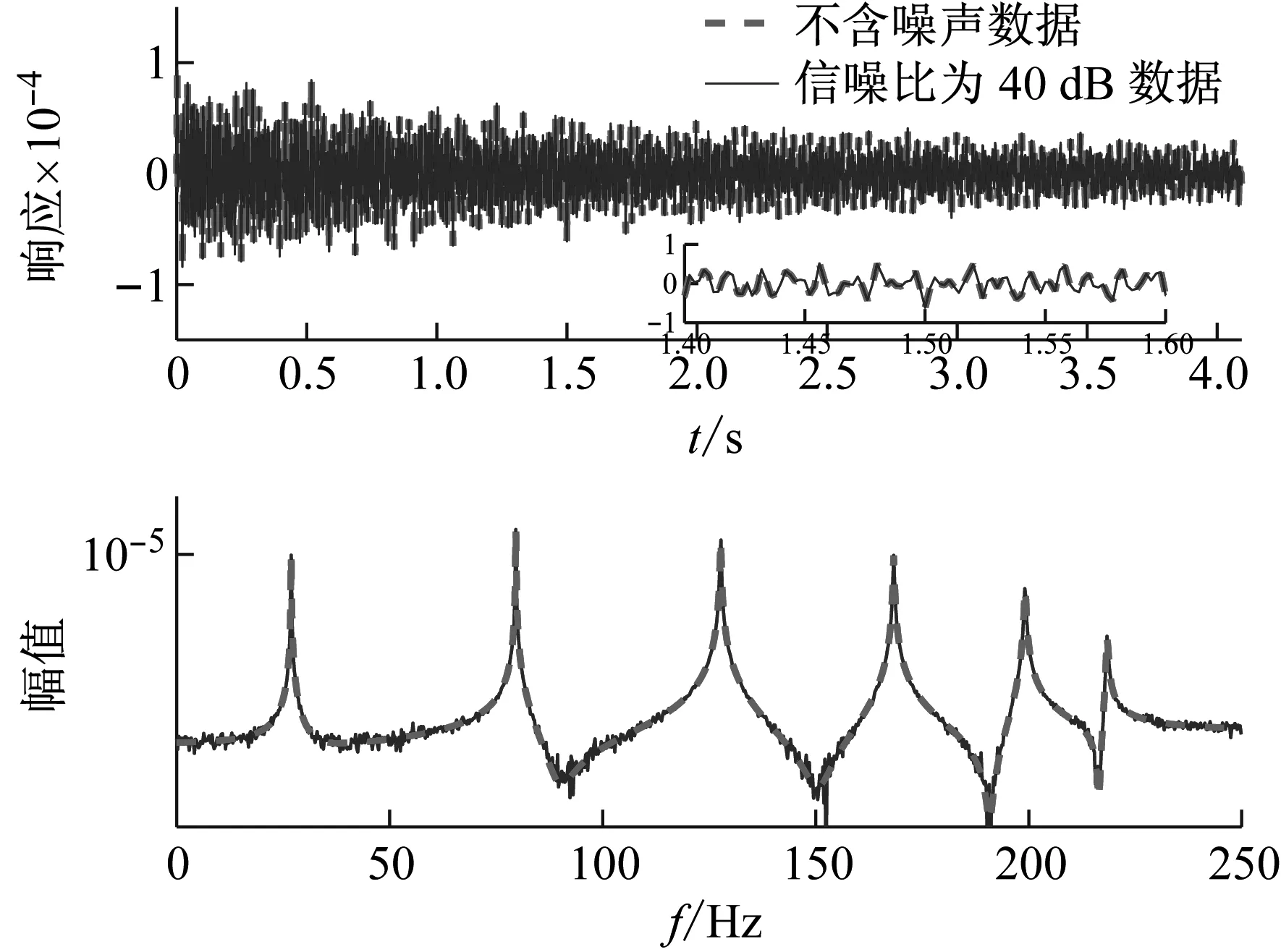
圖3 不含噪聲信號與含信噪比40 dB噪聲的信號時程與頻譜對比

Fig.3 The time domain and frequency spectrum comparison between clear signal and signal containing SNR 40 dB noise

根據頻譜的峰值，分別設置頻率范圍(26.5，27.5)、(79，80)、(127，128)、(168，169)、(198.5，199.5)和(218，219)，6個峰值分別包含于6個頻率范圍之內。將信噪比為40 dB的信號代入式(18)構建Hankel矩陣，根據式(21)得到系統矩陣A，進而計算極值和留數。對極值取模獲得實頻率，根據實頻率選取各頻率范圍內對應的極值和留數，代入式(5)中進行重構，得到消噪后信號。消噪后信號與不含噪聲信號的時程和頻譜對比,如圖4所示。結果表明本文方法能有效消除信噪比為40 dB的噪聲。

為了進一步驗證本文方法消噪效果，將該方法應用于噪聲水平較高的信噪比為10 dB的信號，消噪前后的時程和頻譜如圖5和圖6所示。消噪前第六階頻率幾乎淹沒于噪聲中，消噪后得到的頻譜與不含噪聲的頻譜重合較好，表明本文方法對高噪聲水平的信號也有較好的消噪效果。

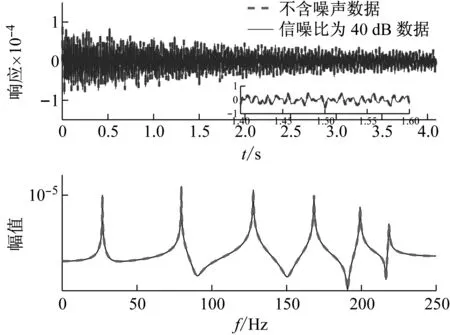
圖4 不含噪聲信號與含信噪比40 dB噪聲的信號消噪后的時程與頻譜對比

Fig.4 The time domain and frequency spectrum comparison between clear signal and signals eliminated noise

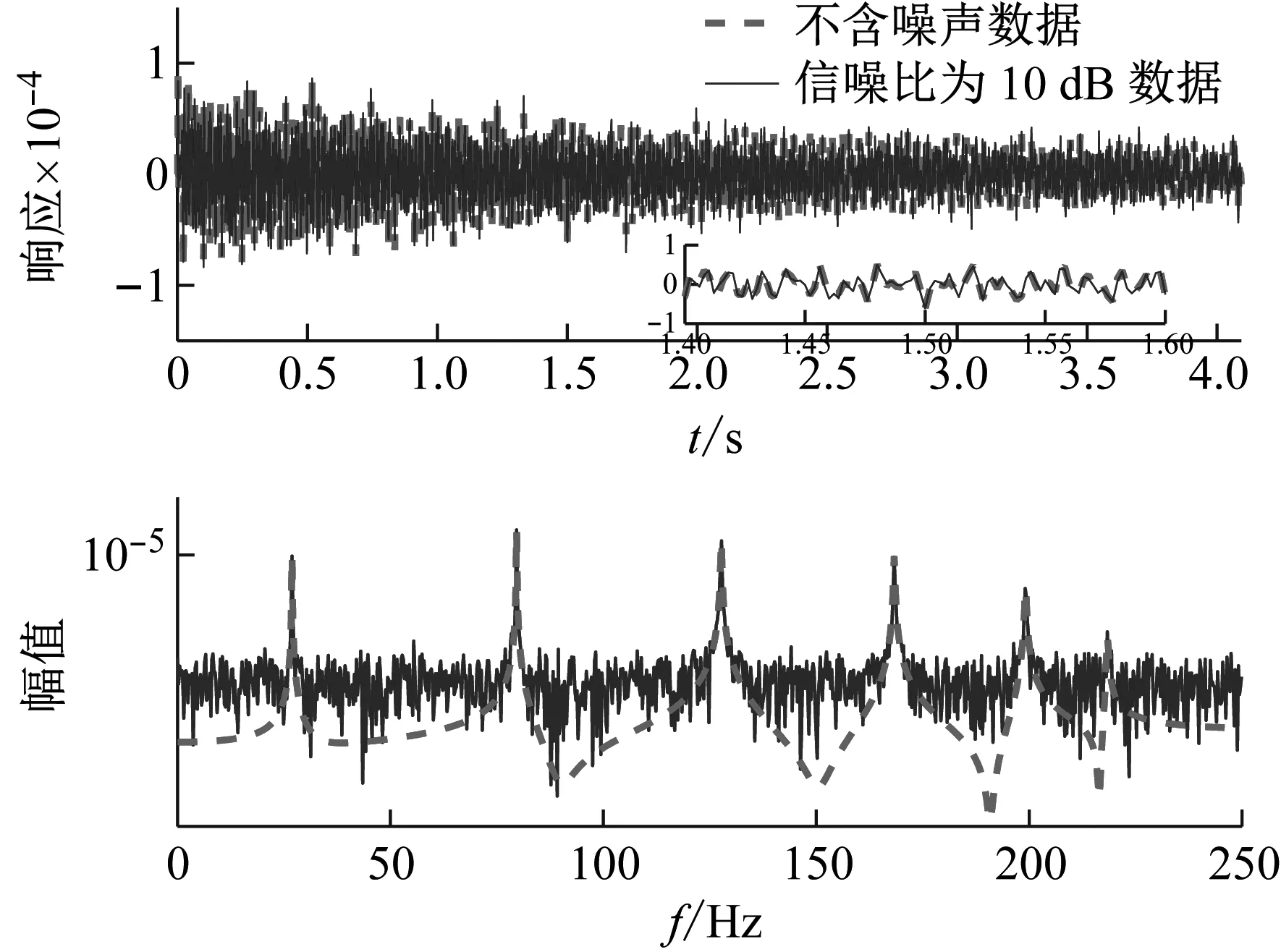
圖5 不含噪聲信號與含信噪比10 dB噪聲的信號時程與頻譜對比

Fig.5 The time domain and frequency spectrum comparison between clear signal and signal containing SNR 10 dB noise

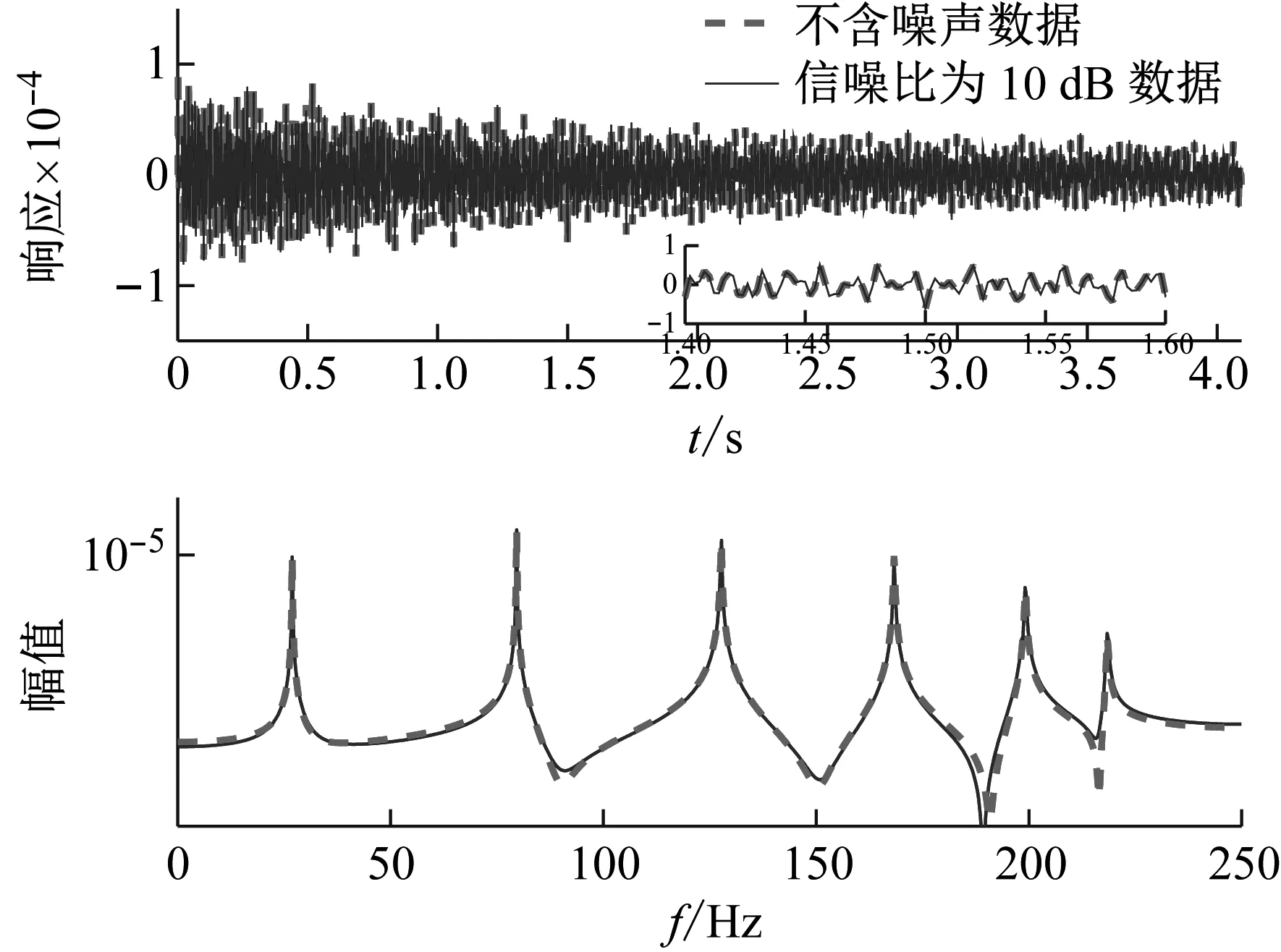
圖6 不含噪聲信號與含信噪比10 dB噪聲的信號消噪后的時程與頻譜對比

Fig.6 The time domain and frequency spectrum comparison between clear signal and signals eliminated noise

為了定量分析本文方法的消噪效果，引入噪聲抑制率(Noise Suppression Ration, NSR)、信號失真率(Signal Distortion Ratio, SDR)[13]和決定系數(Coefficient of Determination)三個指標。

NSR=

(28)

(29)

式中：s(n)為不含噪聲信號；f(n)為添加噪聲后f′(n)為消噪后信號。

(30)

對于信噪比為40 dB的信號，本文消噪方法消噪后的噪聲抑制率為0.797 8，信號失真率為0.002 008 4，決定系數為0.999 96。運用本文方法分別對含信噪比為30 dB、20 dB和10 dB噪聲的信號進行消噪，其噪聲抑制率和信號失真率列于表1中，消噪前后的決定系數如圖7所示。對比文獻[13]，其提出的消噪方法的噪聲抑制率為0.872 7，信號失真率為0.174 4。本文方法消噪后得到不同噪聲水平的噪聲抑制率都約為0.8，信號失真率隨著噪聲的增大而逐漸增大，但總都維持在比較低的水平；消噪后的決定系數R2都大于0.995，隨著噪聲水平的提高，決定系數R2逐漸減小。三個指標的分析結果表明本文的消噪方法消噪效果較好。

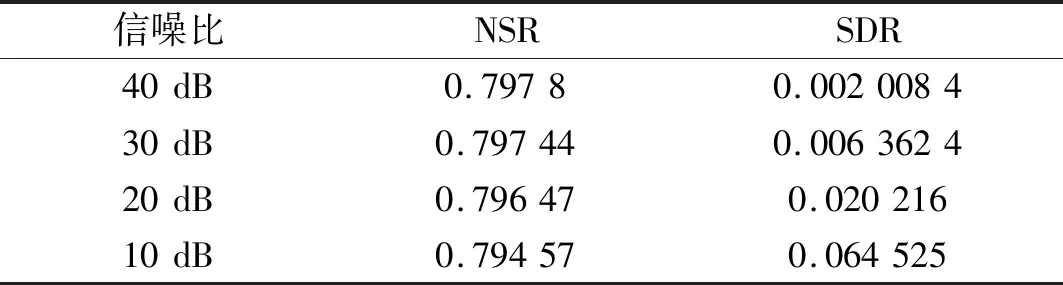
表1 不同信噪比信號的噪聲抑制率(NSR)和信號失真率(SDR)

4 實測數據應用

海洋結構物實測振動響應信號往往含有較高水平的背景噪聲，尤其環境激勵下其結構固有模態往往淹沒于噪聲之中，導致結構動力特性識別困難。為研究方法的有效性，選用冰擊激勵作用下的某海洋石油平臺(見圖8)實測數據進行研究。結構振動測試時，使用三向加速度傳感器采集其加速度響應信號,傳感器安裝位置如圖9所示。采樣頻率為200 Hz。選取主振動方向300～320 s的實測數據進行分析，其加速度響應時程如圖10所示。對加速度響應數據進行傅里葉分析，得到頻譜如圖11所示。由于海洋平臺實際環境激勵情況比較復雜，激勵能量較弱，得到頻譜非常復雜，包含大量噪聲成分。這些噪聲使響應信號的進一步分析面臨很大困難。

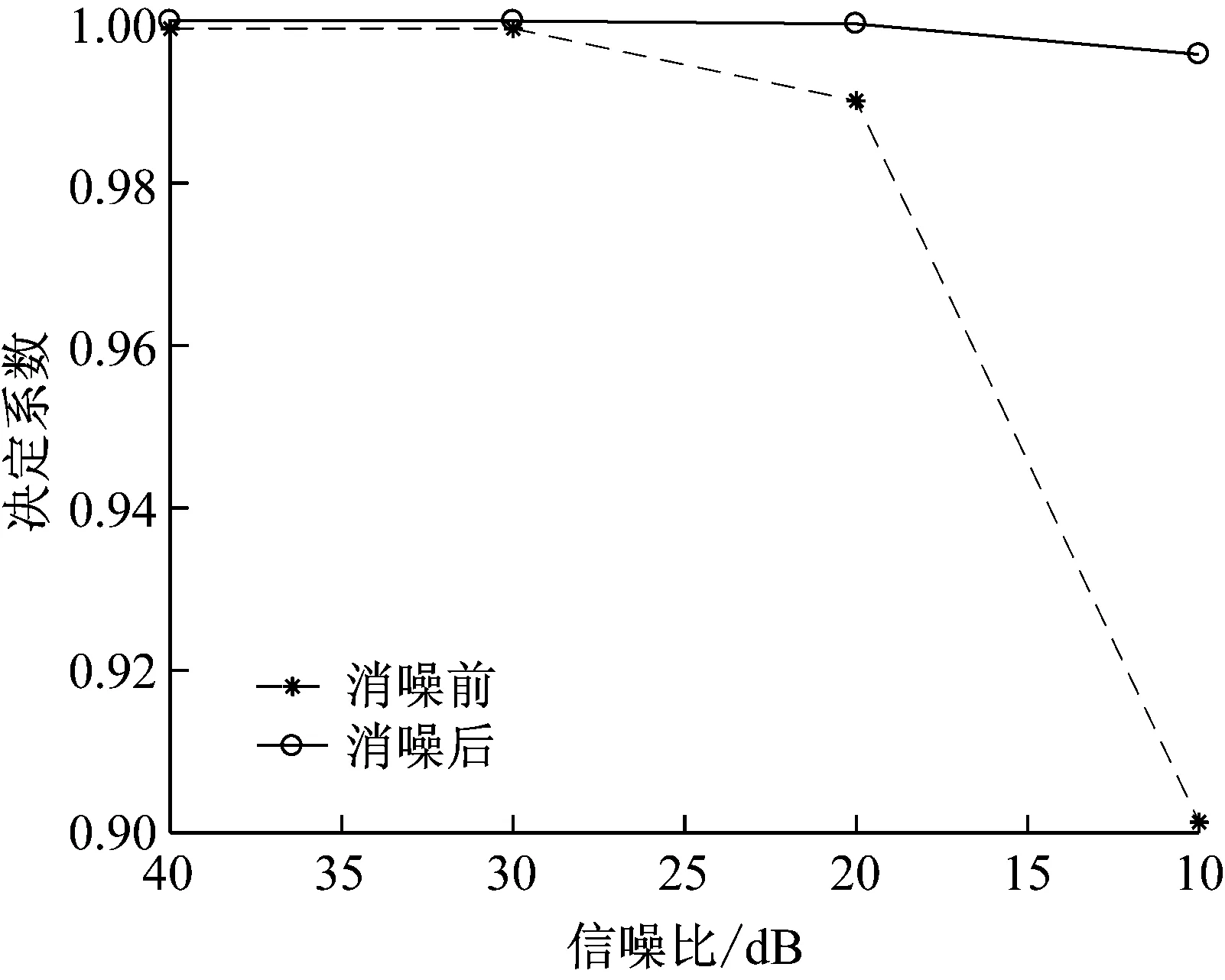
圖7 決定系數隨信噪比變化

圖8 海洋石油平臺

圖9 加速度傳感器安裝位置

1994年，該平臺所有單位對其進行了振動檢測，應用傳統的頻譜分析技術，得到該石油平臺的前2階頻率，分別為0.9 Hz、1.15 Hz與1.175 Hz。考慮到該平臺至今仍在服役，其結構固有特性相對穩定。故將應用本文方法對圖10所示信號進行消噪處理。設置頻率窗口為0.8～1.3 Hz，并采用獲取圖5同樣的技術流程，可以得到消噪后的信號，其頻譜如圖12 所示。從圖12可知，實測原始信號中小于0.8 Hz、大于1.3 Hz的頻率成分被成功剔除，其0.8～1.3 Hz范圍內有2個明顯的峰值，峰值處對應的頻率分別約為0.85 Hz和0.95 Hz。為進一步驗證消噪信號的正確性，對其應用ERA方法進行模態參數識別，其結果為0.916 19 Hz和1.036 7 Hz，相對1994年結果計算精度得到大幅提高。

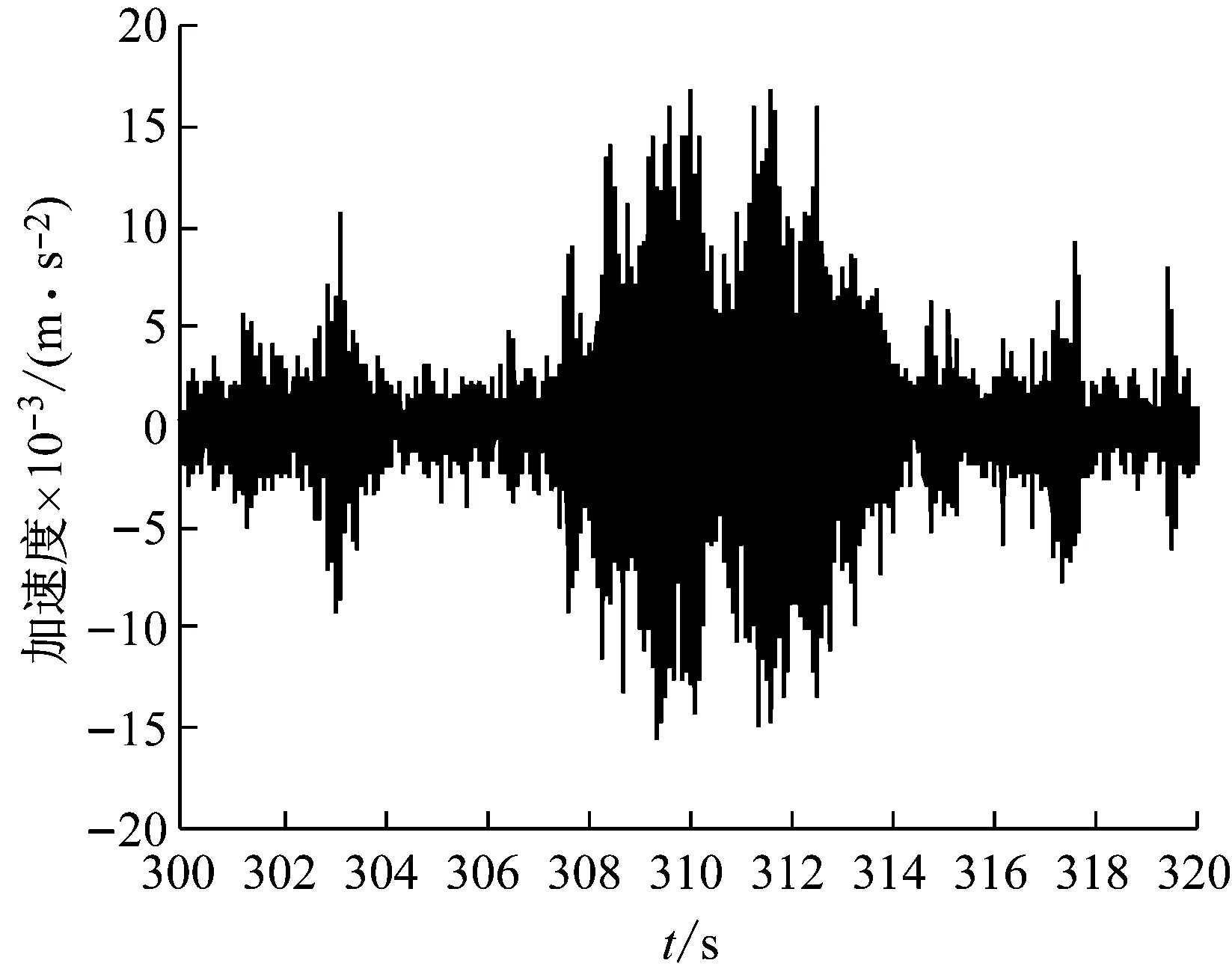
圖10 加速度響應信號

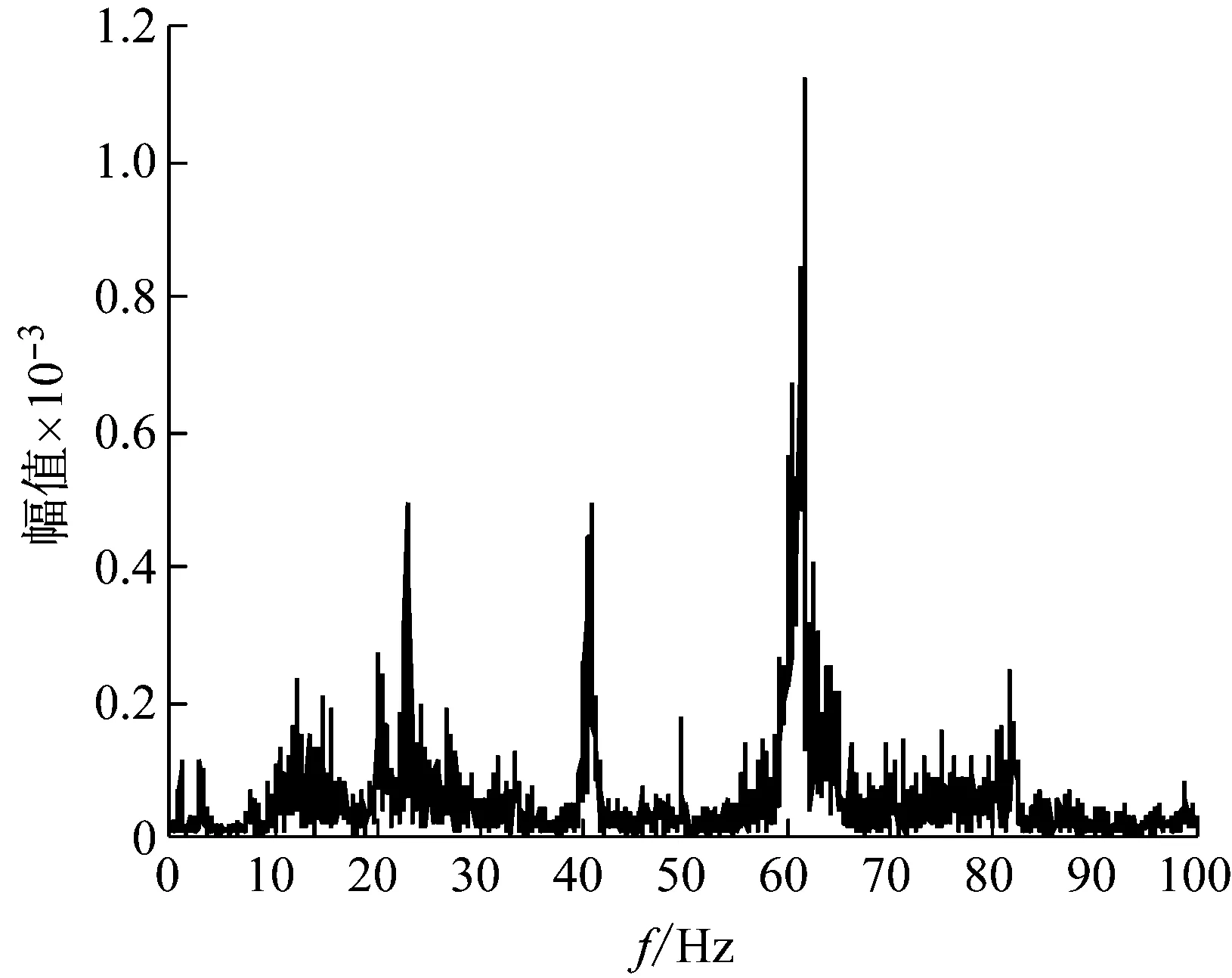
圖11 頻譜圖

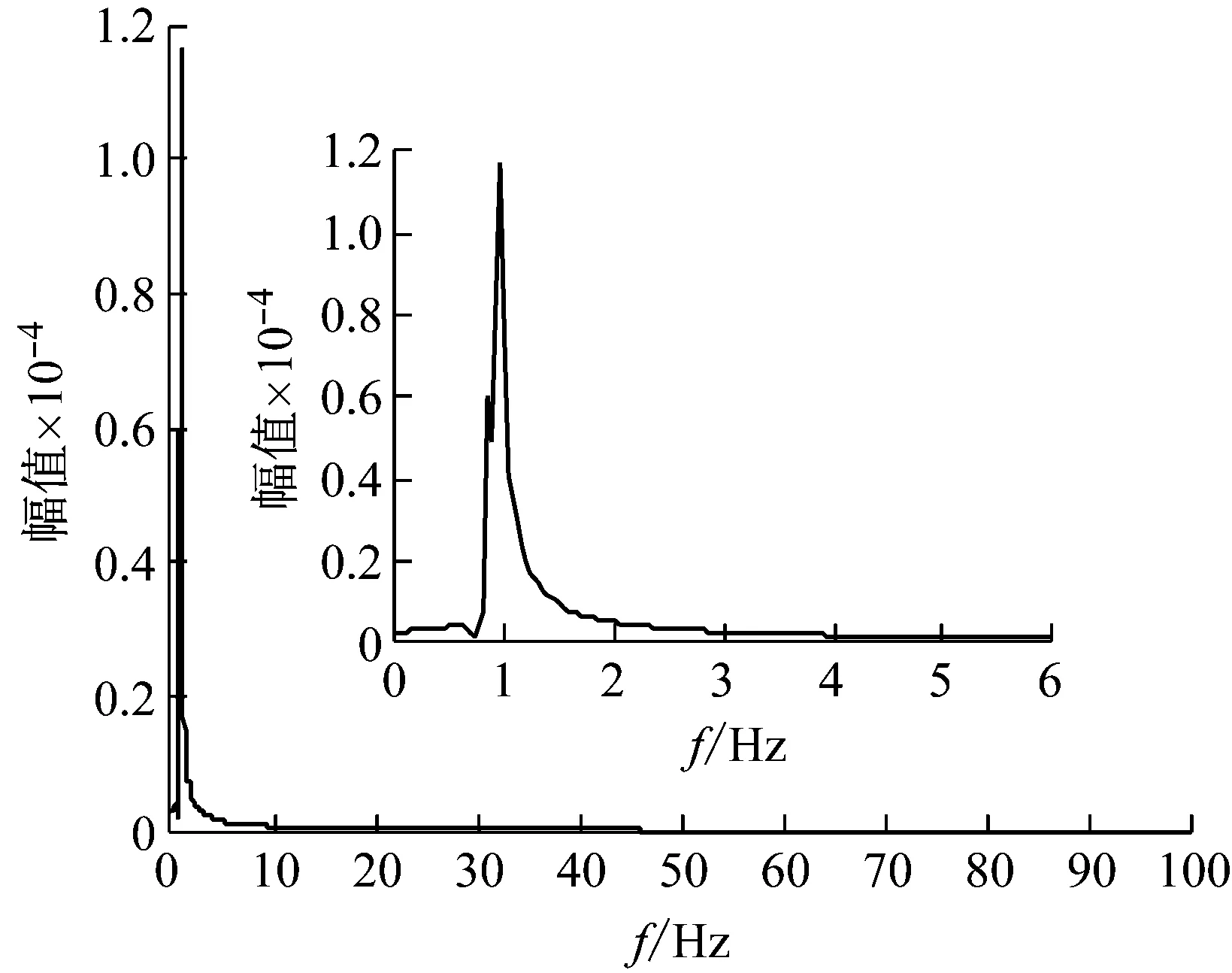
圖12 消噪后頻譜圖

5 結 論

本文從信號分解的角度提出了一種基于極值-留數的信號分解消噪方法，解決了實際工程中在遭遇高背景噪聲其結構固有信息往往被當作環境噪聲而剔除的問題。選用的6自由度質量-彈簧-阻尼系統已經證實：當信噪比(SNR)分別為40 dB和10 dB時，消噪后信號與不含噪聲信號的時程圖和頻譜圖幾乎重合，表明該方法能有效消除信號中強噪聲的干擾。計算獲得的不同信噪比下的噪聲抑制率(NSR)和信號失真率(SDR)，NSR約為0.8，SDR維持在較低水平，當噪聲能量變化較大時，使用本文方法消噪得到的NSR變化較小，SDR較大。不同信噪比下，消噪后信號與不含噪聲信號的決定系數都大于0.995，表明消噪效果較好。為研究方法的有效性，選用了冰擊激勵作用下的某海洋石油平臺實測數據進行研究，獲得了預期頻率區間的頻率成分，基于此進行模態參數識別，可以大大提高模態參數識別精度，具有潛在的工程應用價值。