一種適用計算聲學問題的網格間斷人工黏性分布策略
王 鑫, 余培汛, 楊 海, 潘 凱
(中國飛機強度研究所 航空聲學與動強度航空科技重點實驗室, 西安 710065)

抑制短波的有效手段主要有兩種:① 迎風格式,通過固有的耗散性來抑制短波,該方法的不足之處在于無法識別短波長波范圍,將兩者一起耗散,這樣影響到計算結果的準確度;② 在對稱模板的差分方程中添加人工黏性項,所選擇的人工黏性項必須在有效抑制短波的同時,保證對長波的影響很小。Tam在1993年提出了人工選擇耗散法[3],通過對人工黏性耗散項的系數選擇,使得其耗散項只對短波起作用,而對長波幾乎沒有影響,用于氣動聲學計算時取得了很好的結果。但是該方法只限于均勻對稱網格,尚未在非均勻網格中進行拓展。Engquist[4]提出用非線性濾波法來捕獲激波的方法,它在每一時間步用一個非線性過濾因子對數值解進行處理,只作用在部分網格點上。王澤暉等[5]在Bjrn提出的非線性濾波法基礎上,根據一個檢驗函數,分析了非線性濾波效率與波長的關系,并引入了具有TVD性質的非線性濾波法,通過數值算例驗證了DRP格式與非線性濾波法結合的可行性,表明該方法對于在網格交界面、初始值間斷、非線性聲波傳播等計算氣動聲學常見情況下產生的短波有很好的抑制作用。該方法對短波具有很好的抑制作用,但同時對長波的耗散也相對較大,影響數值的計算精度。
本文在直角坐標人工選擇耗散法的基礎上,將其轉換成曲線坐標系下的表達形式,并在多塊網格交界面處、交界點、出口邊界等處按照當地網格雷諾數的倒數進行正態分布,并通過NASA標模算例進行了該方法的驗證分析。
1 數值模擬方法
1.1 線化歐拉方程
本文的主動控制方程采用的是二維線化歐拉方程作為聲傳播方程,其表達形式如下
(1)
式中:Q0=(ρ′,u′,υ′,p′)T為瞬時變化量(密度,速度分量和壓力)。Q0=(ρ0,u0,υ0,p0)T為時均變量。式(1)的矩陣系數表示為
(2)
式中:γ=1.4為比熱比,S為聲源項。
經過曲線坐標轉換后,式(1)可寫為下式
(3)

1.2 空間離散格式
計算氣動聲學所要模擬的是物理波的傳播過程,為此所選擇的差分格式要能準確反映其傳播特征(色散性,耗散性,方向性,相速度,群速度等)。高階泰勒級數截斷法所獲得的差分模板關注的是聲波的耗散性。它能準確的逼近物理波的幅值,保證波幅計算值與實際值偏差較小。但對于聲傳播問題,差分格式不僅需要關注聲波的幅值,而且需要關注如何準確描述聲波的傳播,降低振蕩,避免發散。
本文在對于式(1)中通量項的離散采用了Tam提出的7點DRP差分格式,其x方向的通量項可表示為式(4),其余兩個方向的通量采用同樣的差分格式。
(4)
其中,插值系數為
(5)
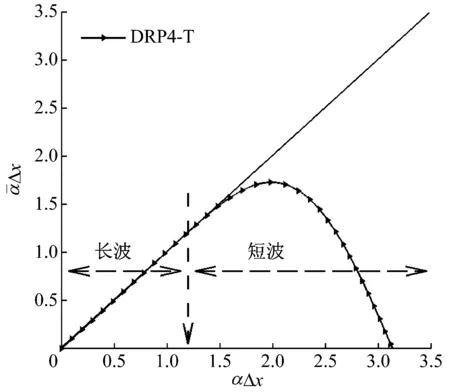
圖1 有效波數隨波數變化曲線(Tam方法)
1.3 無反射邊界條件
在計算氣動聲學中,由于受到計算資源的約束,計算區域不可能無限大,因此需要人為地在計算區域中采用一種邊界條件來取代遠場區域的信息。這種取代遠場區域的邊界條件,其需要起到兩個作用:① 讓計算區域內的各種物理波能無反射的通過邊界;② 讓邊界以外的任何擾動不能傳入計算區域,防止污染數值解。
論文中采用了Hu所提出的PML(Perfectly Matched Layers)邊界條件,對無分裂形式的PML方程[7-9]在曲線坐標上進行了轉化,并改善邊界條件的數值離散格式,增強其穩定性。
遠場邊界處的二維LEE(Linearized Euler Equations)方程組通過擬線性化處理,可寫為
(6)
根據Hu的方法,可知由于對流效應,波的相速度和群速度可能沿著不同的方向發展。如果此時在PML方程中僅引入數值黏性,反射波將不能完全被消除,以致計算的穩定性受到影響。為了解決這一難題,Hu采用了保持空間不變而對時間進行變換的方法,即:
(7)
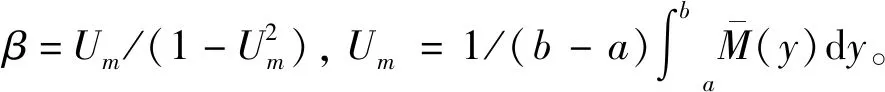
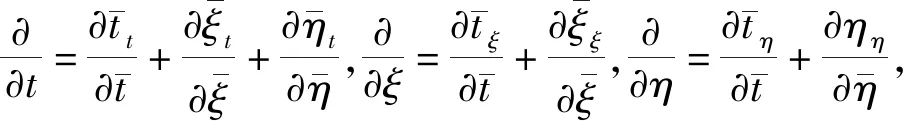
(8)
將其代入到式(6)中,可得以下方程
(9)
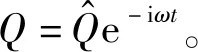

(10)
然后通過復數變易法,引入阻尼,即:
(11)
將式(11)代入式(10)可得
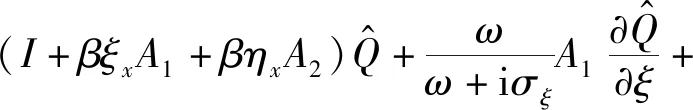
(12)
式(12)兩端同時乘以(ω+iσξ)(ω+iση)/ω2,可得式(13),即:
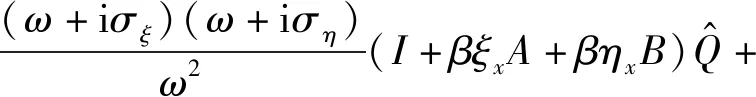
(13)
傅里葉逆變換得
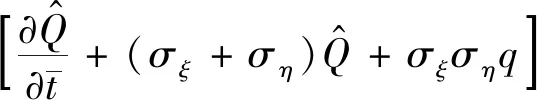
(14)

(15)
將上述偏導數關系式(15)代入式(14),展開可得:
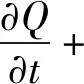
(σξ+ση)Q+σξσηq+βQ(σξξxA1+ηxA2ση)+
β(ξxA1+ηxA2)σξσηq=0
(16)
2 曲線坐標系下人工黏性在間斷處的分部策略
對于聲學問題的數值模擬,在劃分網格的過程中不可避免地帶來網格間斷等問題。而這些間斷(物面邊界、遠場邊界、網格交界面)易引起差分格式的色散,產生數值偽波。以物面邊界為例,對于空間離散采用7點DRP格式,假如物面不采用虛網格的形式,如圖2所示。垂直于物面的網格點A、B空間離散將無法采用對稱模板的7點DRP格式。為此在添加人工黏性項時,網格點A、B的人工黏性模板也是有所區別的,對于物面上方網格點A采用3點人工黏性模板,網格點B采用5點人工黏性模板,網格點C和D采用7點模板。網格交界面處可通過采用3層虛網格添加7點模板的人工黏性項,也可類似于物面邊界方式處理(注:程序在網格交界面采用了3層虛網格的形式)。
另外為了保證計算的穩定性,在公共邊的奇異點(非常規的1-1交接網格頂點處)附近需要添加額外的人工黏性項,如圖3所示。接下來將介紹程序中在網格內部、網格交界面、物面邊界、公共邊奇異點處所采用的人工黏性項分布方式。

圖2 間斷處的人工黏性函數分布示意圖
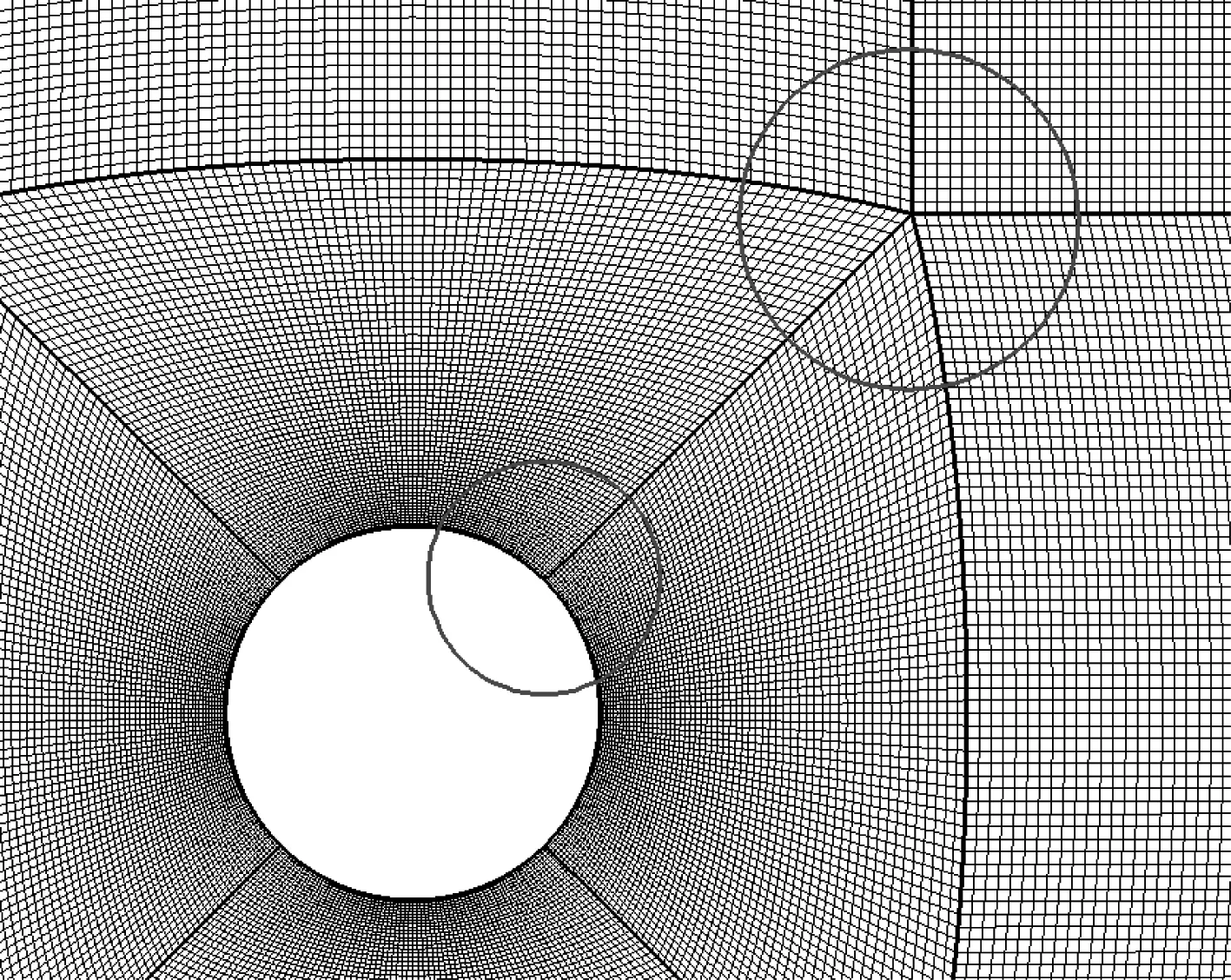
圖3 奇異點示意圖
假設采用7點人工黏性模板,在一維控制方程中,添加人工黏性項后,可表示為
(17)
其中RΔx=a0Δx/υa,為單位網格雷諾數。當網格存在拉伸和變形時,即計算坐標與直角坐標不一致,存在坐標變換時,式(18)中人工黏性的添加需要轉換到計算坐標系下
(18)
如果保證式(17)與式(18)中人工黏性添加的效果相同,需使得RΔξ=xξRΔx。Δξxξ為曲線坐標中長度Δx在計算坐標中相對應的值。與一維方法類似,在三維空間中添加人工黏性可表示為
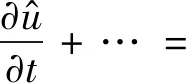
(19)
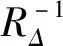
(20)
式中:ξ0為網格邊界處坐標;nΔξ在文中取為當前網格塊在ξ方向的半寬。同理在其余兩個方向網格雷諾數的倒數分布表示為
(21)
(22)
在需要添加人工黏性的奇異點(ξ0,η0,ζ0)上網格雷諾數的倒數分布為
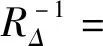
(23)
3 算例驗證
為了驗證曲線坐標系下人工黏性格式的合理性,文中選用了NASA第二屆氣動噪聲會議[11]中初始擾動繞圓柱傳播算例。同時,該算例同時也驗證了遠場無反射邊界條件處理曲面邊界的能力。
如圖4所示,直徑r=1的圓柱的坐標系原點位于圓柱的中心,點A、B、C分別是三個聲壓觀測點,坐標分別為(r=5,θ=90°)、(r=5,θ=135°)、(r=5,θ=180°)。在距離原點r=4處分布了一個人工點聲源S,其初始賦值如下
(24)
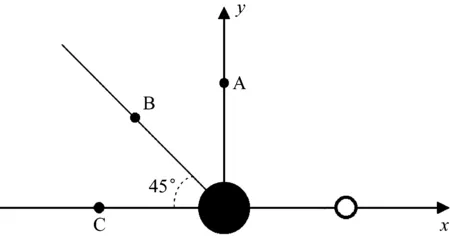
圖4 圓柱計算模型示意圖
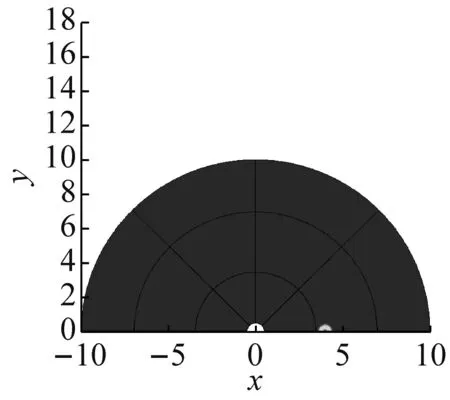
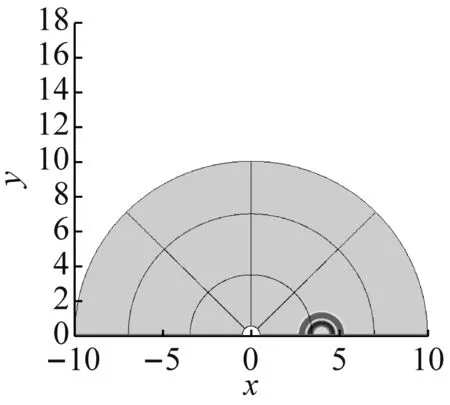
圓柱壁面采用的是滑移邊界條件,遠場采用的是無反射邊界條件。對于控制方程的離散,采用7點模板的DRP格式,人工黏性的分布策略如圖5~圖7所示,從網格塊邊界向內部網格雷諾數的倒數逐漸降低。文中計算網格的最小尺度為0.01,聲場計算采用統一的無量綱時間步長Δt=0.002。圖8(a)、圖8(b)、圖8(c)、圖8(d)分別為t=50Δt、t=500Δt、t=2 000Δt、t=5 000Δt四個時刻的聲傳播布云圖。從圖8可知,聲波隨著時間推移,向空間逐步散開。當聲波到達圓柱時,聲波會發生部分反射現象,形成二次聲源向空間傳播。

圖5 ξ方向無量綱分布


圖6 η方向無量綱分布


圖7 奇異點處無量綱分布
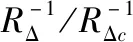
(a) t=50Δt
(b) t=500Δt
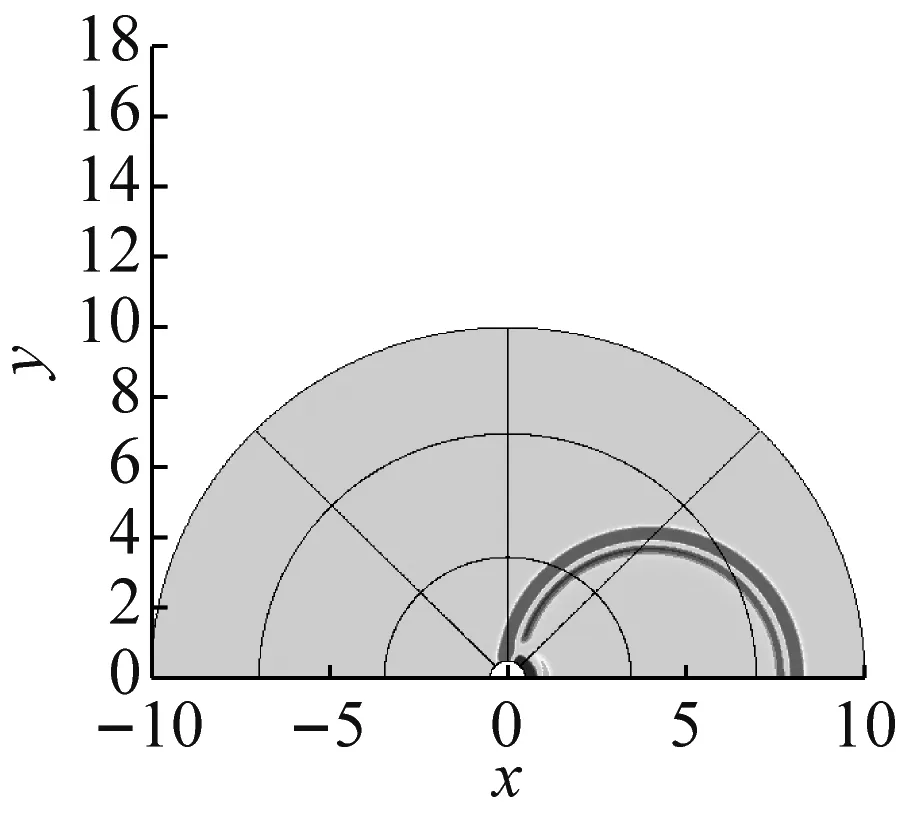
(c) t=2 000Δt

(d) t=5 000Δt
圖8 不同時刻的聲傳播云圖
Fig.8 Schematic diagram of sound propagation at different times
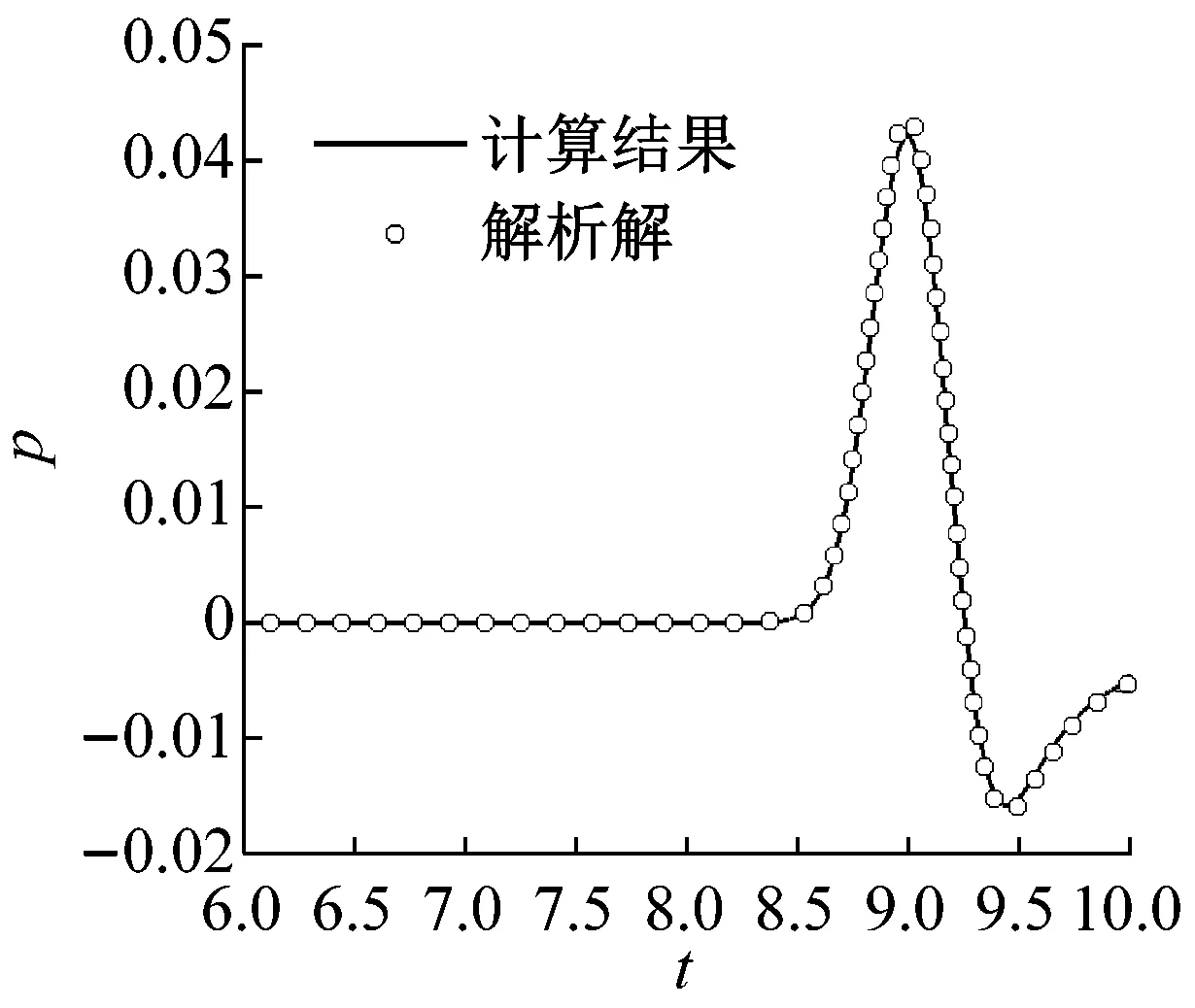
為了定量上對比分析所采用的人工黏性項分布方式的合理性,圖9(a)、圖9(b)、圖9(c)分別表示觀測點 A、B、C處的聲壓隨時間的變化曲線。圖9同時給出了計算解和解析解,其中圓圈表示解析解,實線為計算結果。由圖9可知,文中計算得到的結果與解析解吻合得很好,對比結果說明了聲波傳播程序添加人工黏性項的合理性及處理曲邊邊界能力。

(a) A處
(b) B處
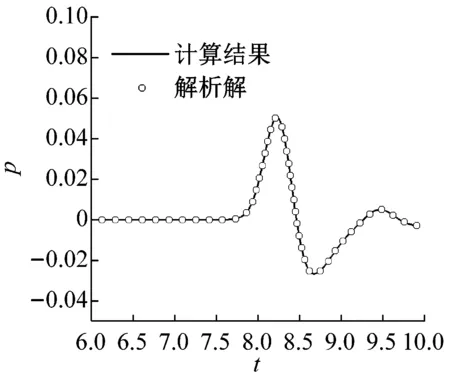
(c) C處
圖9 觀測點處聲壓隨時間變化曲線
Fig.9 Curve of sound pressure at observation point
4 結 論
通過文中理論的闡述及算例的驗證分析,可得出以下結論:
(1) 本文基于笛卡爾坐標系的人工黏性添加策略推導了曲線坐標系下的表示形式,并通過在網格間斷等處的正態分布策略,提出了一種適用于網格間斷處的人工黏性添加策略,通過標模算例的計算分析驗證了該方法可成功應用于曲線坐標系下復雜網格的計算聲學短波發散問題中。
(2) 針對初始擾動繞圓柱傳播算例中的計算結果,可知聲波首先向空間傳播。當聲波到達圓柱時,形成二次聲源向空間傳播。這一聲傳播現象以及監測點的對比分析,在驗證網格添加策略合理性的同時也驗證了遠場PML邊界條件的無反射特性。

