水下爆炸沖擊波作用下屏蔽裝藥的沖擊引爆理論和仿真研究

李元龍, 王金相, 申向軍, 周 楠, 黃瑞源， 榮 光

(1.南京理工大學 瞬態物理國家重點實驗室，南京 210094； 2.晉西集團753廠，山西 太谷 030800； 3.南京森林警察學院 刑事科學技術系，南京 210023)

目前魚雷是水面艦艇的主要威脅之一，因此開展有效的反魚雷技術研究關系到水面艦艇的生存。隨著反魚雷技術的日趨發展，水下爆炸沖擊波逐漸成為毀傷魚雷的最主要形式之一，而魚雷戰斗部裝藥則是毀傷的主要針對部分[1]。因此，研究水下爆炸沖擊波對屏蔽炸藥的毀傷對于硬毀傷魚雷技術具有重要的意義。Cole[2]根據大量水下實驗數據提出了經典的水下爆炸經驗公式，為水下爆炸載荷的計算提供了簡潔實用的方法，Zamyshlyayev[3]則在Cole的基礎上，綜合運用理論和試驗的方法，對經驗公式進行了改進。當前，對于破片撞擊屏蔽炸藥的沖擊引爆問題，已開展了大量的研究[4-6]，從理論以及數值模擬方面建立了屏蔽炸藥的臨界起爆判據[7-9]，很好的描述了屏蔽炸藥的起爆特性, 為沖擊起爆實驗和后續的可靠性研究提供了大量的參考。但這些研究大多應用于空氣中屏蔽裝藥的起爆問題，而涉及水下爆炸沖擊波的內容還較少。基于水介質中爆炸沖擊波傳播特性，充分考慮沖擊波強度、殼體材料、厚度以及被發炸藥的屬性等因素開展爆炸沖擊波引爆屏蔽裝藥條件研究是當前急需開展的研究方向，并將對反魚雷技術提供一定的指導作用。

本文從理論上建立了水下爆炸沖擊波對屏蔽裝藥的沖擊引爆模型，利用AUTODYN仿真軟件對水中沖擊波的傳播過程和屏蔽裝藥的沖擊引爆進行了模擬，驗證了理論計算模型的有效性，采用最小二乘法得到了臨界起爆判據的參數n、K，分析了主發藥質量和擋板厚度對沖擊引爆PBX-9404炸藥臨界距離的影響。

1 水下爆炸沖擊波對屏蔽裝藥的理論分析

1.1 水下爆炸沖擊波理論

Cole通過對大量實驗數據的整理，總結了水下爆炸沖擊波經驗公式，Zamyshlyayev在其基礎上改進得到峰值壓力公式為

(1)

式中：Pm為沖擊波峰值壓力；W為TNT炸藥質量；R為測點到爆心的距離；R0為炸藥初始半徑。

1.2 沖擊起爆判據

炸藥對沖擊載荷的動態響應分兩種情況：一種是強沖擊載荷下，炸藥沖擊轉爆轟(SDT)；另一種是長持續脈沖時間發生的反應(LALDS)。

在強沖擊波載荷作用下，炸藥發生爆轟準則可表述為

p2τ=K

(2)

式中:p為炸藥界面沖擊波壓力;τ為沖擊轉爆轟的時間;K為與炸藥相關的參數。

在炸藥界面壓力p低于臨界起爆壓力pc情況下，長時間的低壓力沖擊波持續作用也會形成炸藥的爆轟。在這種情況下，沖擊波引發炸藥爆轟準則可表述為

pnτ=K

(3)

從沖擊起爆判據看，具體裝藥均存在一組裝藥臨界起爆特性參數，即臨界起爆壓力pc、能量系數K和經驗常數n。臨界起爆公式廣泛適用于非均質炸藥的一維沖擊起爆，但當在小面積上進行加載時，將出現側向稀疏波，此時，一維短脈沖能量判據就不適用了。因此對水下沖擊波作用進行合理簡化，以便建立理論計算模型。假設水下爆炸沖擊波為一維沖擊波，殼體徑向尺寸遠遠大于沖擊波作用半徑，忽略平行于沖擊波傳播方向的側壁對裝藥的沖擊作用。

1.3 沖擊起爆參數計算

水下爆炸沖擊波沖擊起爆屏蔽裝藥的示意圖如圖1所示。水中沖擊波經過一段距離的傳播到達屏蔽裝藥擋板，在擋板與水的接觸面上發生反射與透射，由于水的波阻抗小于擋板波阻抗，將在水中反射壓縮波，同時，在擋板內透射一壓縮波。設未經擾動的介質參數為p0、ρ0、u0=0，到達擋板界面的沖擊波參數為p1、ρ1、u1、D1，屏蔽擋板厚度為h，沖擊后在水和擋板中產生的沖擊波速度分別為Dw和Dt，水的密度、壓力和質點速度分別為ρw、pw和uw，擋板的密度、壓力和質點速度分別為ρt、pt和ut。沖擊波在水與擋板界面發生作用的示意圖，如圖2所示。

圖1 沖擊起爆示意圖

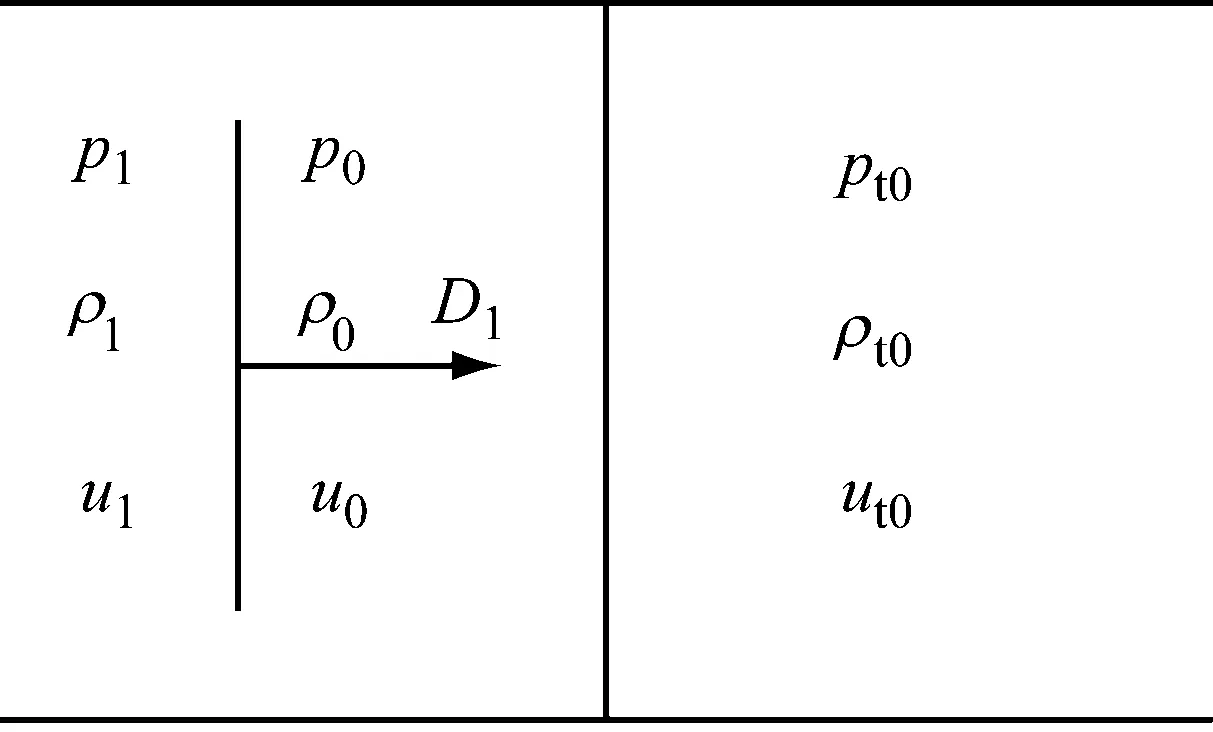
(a) 水與擋板分界面(1)

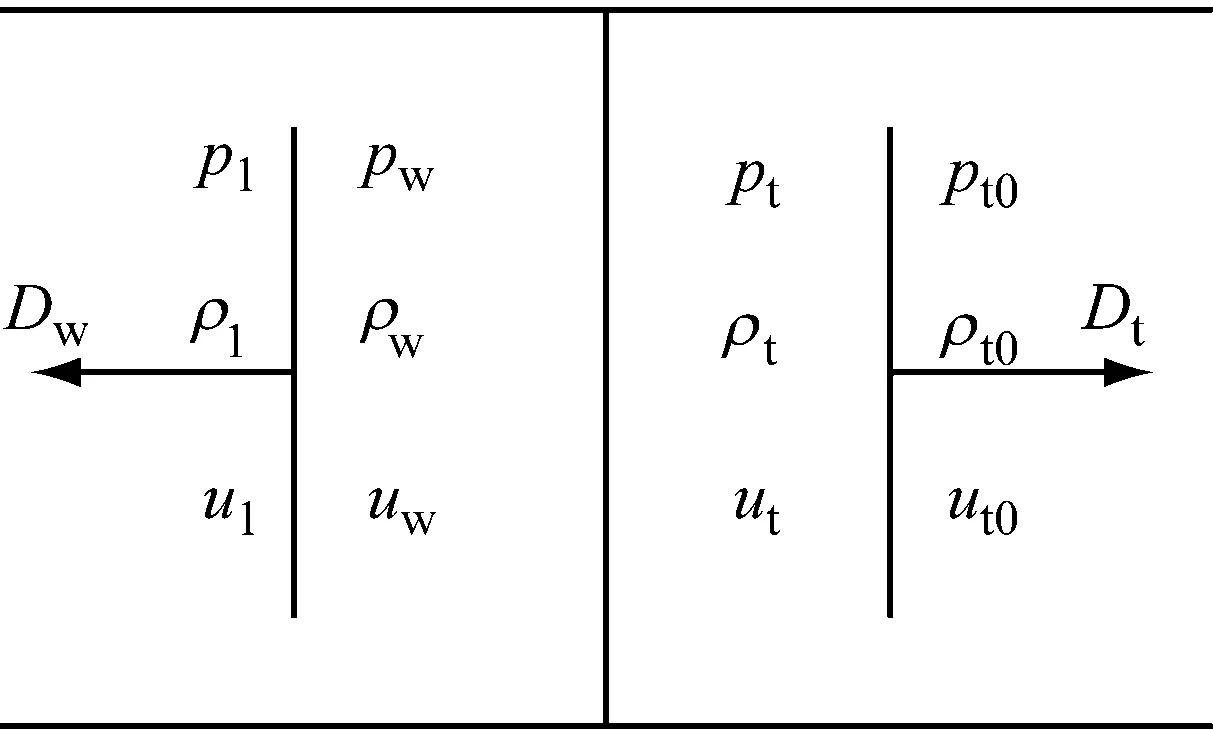
(b) 水與擋板分界面(2)

利用沖擊波前后質量守恒和動量守恒，可得到水和擋板中初始沖擊波壓力表達式

對于水

pw=ρwDwuw

(4)

對于擋板

pt=ρtDtut

(5)

由連續邊界條件可知，沖擊波傳播經過水和擋板的界面時，分界面上的質點運動速度和壓力相等，即

2u1=uw+ut

(6)

pw=pt

(7)

利用線性Hugoniot 關系來表示材料中沖擊波速度與質點速度之間的關系

Dw=aw+bwuw

(8)

Dt=at+btut

(9)

式中：aw、bw和at、bt為根據Hugoniot關系式得出的水和擋板的沖擊壓縮經驗常數。

聯立式(4)～式(9)就可以求出pw、pt、uw、ut。由于擋板材料的波阻抗的作用，沖擊波在擋板中傳播時將會發生衰減，其衰減規律為[10]

pt=pte-αx

(10)

式中：pi為經過擋板衰減后的沖擊波壓力；x為傳播距離(即擋板厚度h)；α為衰減系數。參考式(4) 即可求得相應的質點速度ui。

當擋板中的沖擊波傳播到擋板與炸藥的分界面處，由于炸藥的波阻抗遠小于擋板的波阻抗，在擋板和炸藥的分界面處沖擊波將會產生卸載反射，向擋板反射稀疏波，而向炸藥透射沖擊波。根據炸藥與擋板界面上的動量守恒和連續條件，透射進入炸藥的沖擊波壓力pe及質點速度ue通過下式求得

ρe(ae+beue)ue=ρt[at+bt(2ui-

ue)](2ui-ue)

(11)

pe=ρe(ae+beue)ue

(12)

式中:ae、be為炸藥的Hugoniot參數，理論計算所需參數列于表1[11-12]，其中鋁合金的衰減系數為α=0.029 3 mm-1[13]。

浙江省紀委督導調研組近日在暗訪時發現，有些機關單位的工作微信群和政務辦公群，已經成為形式主義的溫床。因為“干得好不如曬得好”，所以有些基層干部，便把手機當作展示政績的“秀場”。一天到晚，用指尖刷數字、刷進度、刷形象。據說有人為了刷下鄉走訪的里程，還專門到院子里或大街上溜圈。

通過式(10) ～ 式(12) 就可以求出透射到炸藥中的沖擊波壓力。由于透射入炸藥的沖擊波壓力遠遠達不到炸藥的臨界起爆壓力，因此采用考慮長持續脈沖時間的沖擊起爆準則。

表1 材料參數

2 數值模擬模型

2.1 有限元模型

利用AUTODYN軟件進行數值模擬計算，由于各部分關于球形裝藥中心和屏蔽裝藥之間的垂線軸對稱，故采用二維軸對稱計算模型。如圖3所示，主發藥采用TNT球形藥包，半徑為15.7 cm，質量6.6 kg；擋板厚度為h，材料為鋁合金；被發裝藥為PBX-9404炸藥，主發藥處于水介質中。網格采用Euler計算方法，單元尺寸為2 mm，共550 000個單元，炸藥與擋板共節點。為減小爆炸過程中的邊界反射效應，在水、擋板和被發藥的相關位置定義流出邊界條件。

圖3 仿真計算模型

2.2 材料模型與狀態方程

擋板的材料采用Shock狀態方程，材料模型為Johnson-Cook模型，材料參數取自AUTODYN標準數據庫[14]。水的狀態方程采用線性多項式方程[15]，當水壓縮時(μ>0)，其狀態方程為

P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

(13)

當水膨脹時(μ<0),其狀態方程為

P=T1μ+T2μ2+B0ρ0e

(14)

當水既不壓縮也不膨脹時(μ=0)，式(14)和式(15)可以簡化為同一形式

P=B0ρ0e

(15)

式中：P為水中壓力；μ為壓縮比，μ=ρ/ρ0-1；e為水的內能；ρ0為水密度，取ρ0=1.00 g/cm3。A1=2.20 GPa，A2=9.54 GPa，A3=14.57 GPa，B0=0.28，B1=0.28，T1=2.20 GPa，T2=0。

主發藥采用JWL狀態方程，JWL狀態方程定義壓力為相對體積V和單位初始構形體積內能E的函數

(16)

式中：p為壓力；V為相對體積；E為內能；ω、C1、C2、R1、R2為表征炸藥特性的常數。取ρ0=1.63 g/cm3，C1=37.12 GPa，C2=3.231 GPa，R1=4.15，R2=0.95，ω=0.30。

PBX-9404炸藥的狀態方程采用Lee-Tarver點火增長模型，其相關參數見表2，此方程可較好模擬非均質炸藥的沖擊起爆特性[16]

G1(1-F)cFdPy+G2(1-F)eFgPz

(17)

表2 PBX-9404材料參數

式中，F為炸藥燃燒質量分數，它在模擬爆轟過程中控制著炸藥化學能的釋放；I、b、a、x、G1、c、d、y、G2、e、g、z為參數；炸藥反應物與未反應物均采用JWL狀態方程。

3 分析與討論

3.1 理論方法與數值仿真一致性分析

理論計算模型如示意圖1所示。主發藥TNT質量為6.6 kg,半徑R0=9.9 mm，擋板厚度為h，主發藥包與擋板的距離為R。理論計算結果與數值計算結果見表3。通過調整藥包與擋板距離R和擋板厚度h，分析10種不同工況下對屏蔽炸藥起爆的影響。將數值模擬中到達擋板壓力p1、透射入炸藥壓力pe與理論計算結果進行對比，其中到達擋板壓力仿真值與理論值最大誤差為11.52%，透射入炸藥壓力仿真值與理論值最大誤差6.75%，吻合較好，說明所建立的理論計算模型和數值仿真是一致的。

表3 數值模擬結果與理論計算結果對比表

3.2 沖擊起爆過程描述

圖4給出了距離主發藥包1 m處，沖擊引爆被發炸藥的典型爆炸壓力云圖，模型擋板厚度為10 mm。被發炸藥爆炸與否利用炸藥中的壓力及被發炸藥的反應狀態來進行判定。初始主發藥被引爆，形成的爆炸沖擊波在t=460 μs時到達屏蔽擋板，此時沖擊波壓力峰值為125 MPa，經過擋板的透射以及衰減作用傳入被發炸藥，沖擊波在被發炸藥中經過256 μs的時間后，到達被發藥的臨界起爆能量值并將被發炸藥引爆，形成一個強壓力的波陣面迅速向炸藥層內傳播。

(a) t=70 μs

(b) t=200 μs

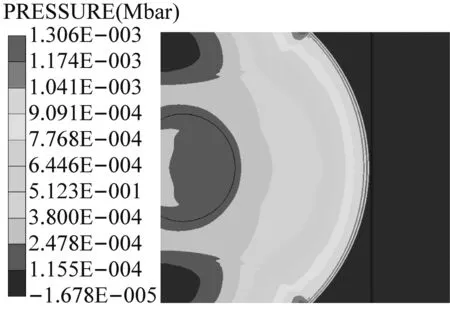
(c) t=460 μs

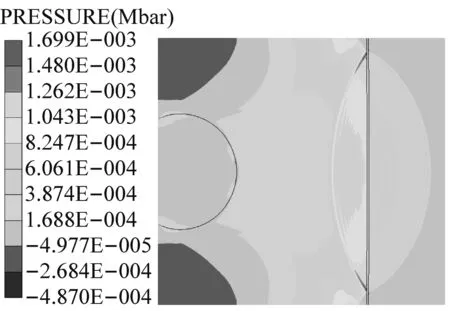
(d) t=580 μs

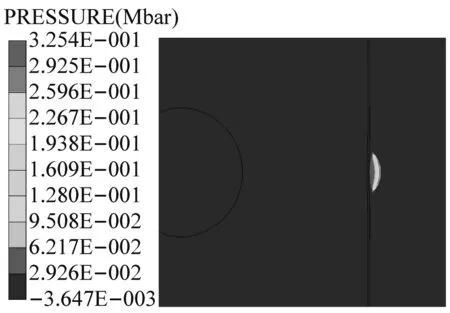
(e) t=720 μs

(f) t=740 μs

圖4 不同時刻沖擊波壓力云圖

Fig.4 Different time pressure shock wave cloud

圖5為擋板附近不同位置的壓力時程曲線，以水與擋板接觸面為z=0，從圖5可知，當沖擊波傳至擋板時，透射入擋板的壓力有所提升，然后在擋板中傳播又產生了一定的衰減，再次經過擋板與炸藥分界面，透射入炸藥的壓力減小為95 MPa，與理論計算值相差2.92%，經過一段時間的作用，壓力值有了明顯的升高，說明此時炸藥被引爆。

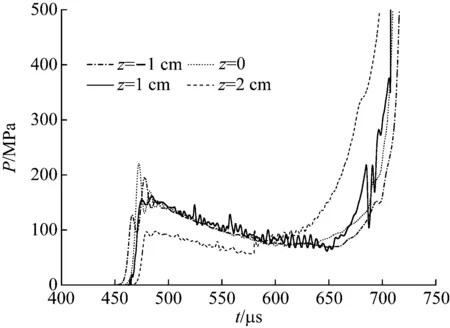
圖5 擋板附近不同位置的壓力時程曲線

3.3 屏蔽裝藥沖擊引爆影響因素分析

隨著主發藥包與擋板之間距離的增加，到達擋板的沖擊波強度逐漸減弱。采用“升—降法”調整此距離可知，在6.6 kg TNT藥量下，主發藥包在距擋板1.6 m處產生的沖擊波不足以起爆被發藥，沖擊波在被發藥中逐漸衰減，在持續時間內達不到臨界引爆乘積要求。

在相同條件下調整擋板厚度，從仿真結果可知，隨著擋板厚度的增加，透射入炸藥的沖擊波強度有所減弱，起爆時間逐漸延長，但引爆乘積變化不大。通過理論判據可以計算出不同屏蔽擋板厚度下，PBX-9404裝藥的臨界起爆距離，圖6給出了臨界起爆距離隨擋板厚度的變化曲線，從圖中可以看出，隨著擋板厚度的增加，由于透射入炸藥的壓力減小，炸藥的臨界起爆距離隨之減小。通過理論計算模型可知，在擋板厚度一定的情況下，不同主發藥量所能引爆屏蔽裝藥的臨界距離不同，圖7給出了臨界起爆距離隨主發藥量的變化曲線。從圖7可知，隨著主發藥量的增加，臨界起爆距離逐漸增加。

由于透射入炸藥的壓力并不能達到臨界起爆壓力，炸藥在低壓力沖擊波作用下經過相對較長的時間才起爆，因此采用第二種形式的沖擊引爆判據pnτ=K，通過參數n、K來描述裝藥的起爆特性。利用表3中的數據，通過最小二乘方法擬合得到n=1.37，K=2.33×107(國際單位制)，與文獻[9]中PBX-9404炸藥的沖擊引爆判據進行比較如圖8，兩者符合較好，在180～390 MPa內誤差不超過15%。因此，利用理論簡化模型以及擬合得到的沖擊起爆判據公式，可以在一定范圍內很好的描述屏蔽炸藥在水下爆炸沖擊波作用下的起爆特性。

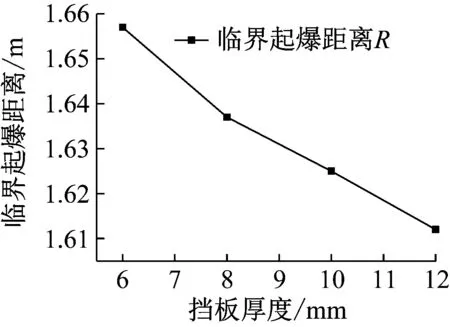
圖6 臨界起爆距離隨擋板厚度變化曲線

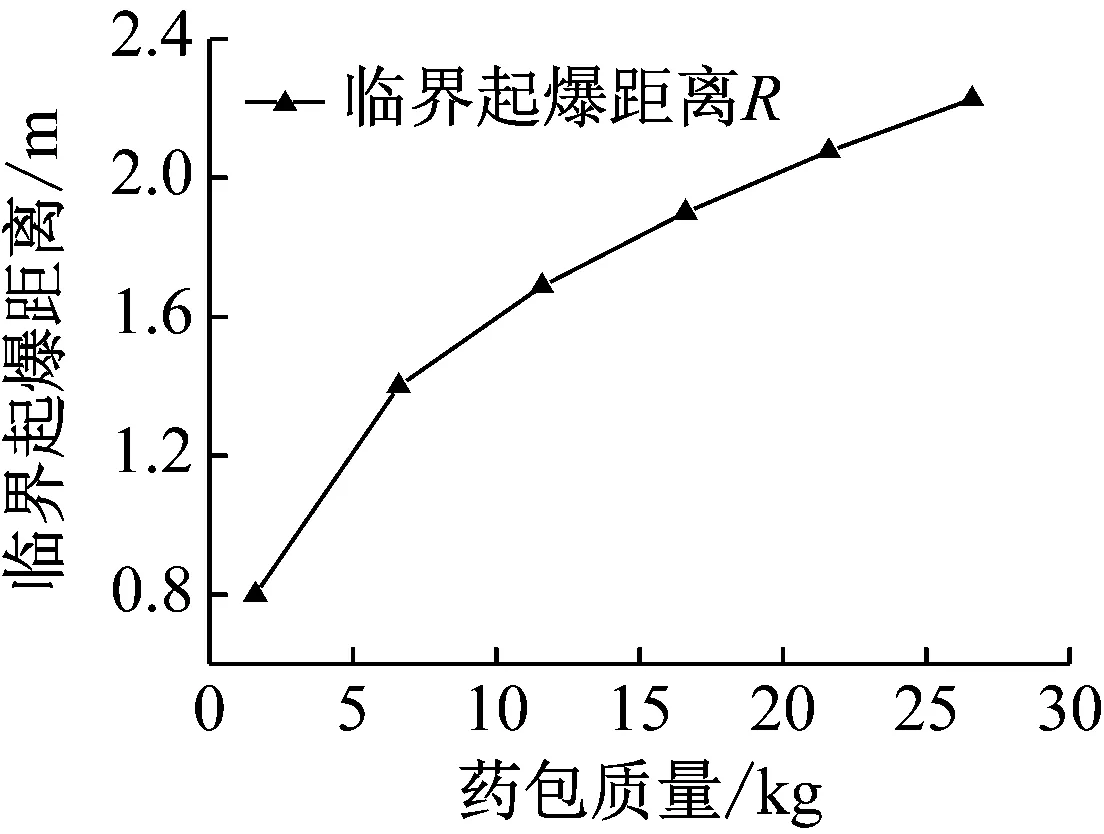
圖7 臨界起爆距離隨主發藥量變化曲線

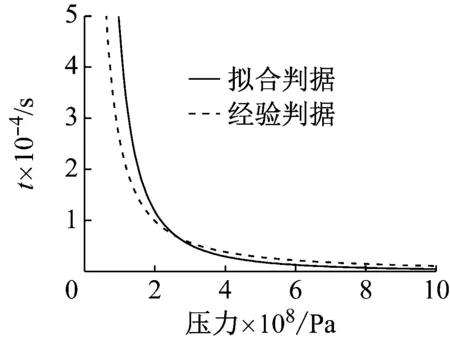
圖8 擬合曲線與經驗曲線對比圖

4 結 論

本文建立了水下爆炸沖擊波對屏蔽裝藥的沖擊壓力計算方法，并利用AUTODYN軟件對所建立的理論計算模型進行了驗證。對不同爆距、不同擋板厚度的爆炸沖擊波沖擊引爆屏蔽裝藥的過程進行了數值模擬，并與理論結果進行對比，得出以下結論：

(1)數值模擬結果與理論計算結果最大誤差為6.75%，吻合較好，說明建立的理論計算模型是有效的。

(2)相同條件下，隨著爆距的增加，透射入炸藥的沖擊波壓力逐漸減小，引爆裝藥的作用時間逐漸增長；在6.6 kg TNT裝藥量下，臨界起爆距離約為1.6 m；隨著屏蔽擋板厚度的增加，透射入裝藥的沖擊波壓力逐漸減小，炸藥的臨界起爆距離隨之減小；隨著主發藥量的增加，臨界起爆距離逐漸增加。

(3)通過最小二乘法得到了簡化理論模型計算臨界起爆判據的參數n、K，使得理論模型可以更好地描述屏蔽炸藥在水下爆炸沖擊波作用下的起爆特性，為沖擊起爆實驗研究和后續的可靠性研究提供一定的理論參考。