三角恒等變換常見典型考題賞析

■張文偉

三角恒等變換是高中數學的重要內容之一，它是每年高考的必考知識點。近幾年高考對三角恒等變換的考查難度有所降低，主要考查三角恒等變換中的公式應用問題、角的變換問題、求值與證明問題。下面舉例解讀這部分的典型考題，供大家學習與提高。

題型一：三角函數公式的應用問題

三角函數公式主要有兩角和與差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式。解題時，要注意三角函數公式的逆用和變形應用，如sinαsinβ+cos（α+β）=cosαcosβ，cosαsinβ+sin（α-β）=sinα·cosβ，tanα±tanβ=tan（α±β）·（1?tanα·

例1若且 3 cos2α=，則sin 2α的值為（ ）。

解：由可 得由α∈可知cosα-sinα≠0，于是可得兩邊平方可得1+，即應選C。

跟蹤訓練1：在斜三角形A B C中，sinA，且則角A的值為（ ）。

提示：由題意可得sinA=sin（B+C）=sinBcosC+cosB·sinC，等式兩邊同除以cosBcosC得tanB因為tan（B+C）=-1=-tanA，即tanA=1，所以應選A。

題型二：角的變換問題

三角函數公式中角的變換與名的變換是三角函數求值中的重要題型，要熟悉角的拆分與組合的技巧，要掌握半角與倍角的相互轉化，如2α=（α+β）+（α-β），α=（α+β）-轉化思想是實施三角變換的主導思想，三角恒等變形要弄清已知式中角的差異、函數名稱的差異、運算結構的差異，從中尋求聯系，實現轉化。

例2已知且則sinβ=____。

解：因為，且cosα所以α+β∈（0，π），

故sinβ=sin[（α+β）-α]=sin（α+β）·

跟蹤訓練2：若α，β都是銳角，且cosα=則cosβ=____。

提示：因為α，β都是銳角，且，所以

故cosβ=cos[α-（α-β）]=cosαcos（α

題型三：輔助角公式的應用問題

函數f（α）=acosα+bsinα（a，b為常數），可化為或其中φ由a，b的值唯一確定。利用輔助角公式可求三角函數的最值、單調區間、周期，這也是高考的常考題型。

例3已知函數f（x）=asin2x+bcos 2x，其中a，b∈R，a b≠0。若f（x）≤對一切x∈R恒成立，且0，則f（x）的單調遞增區間是（ ）。

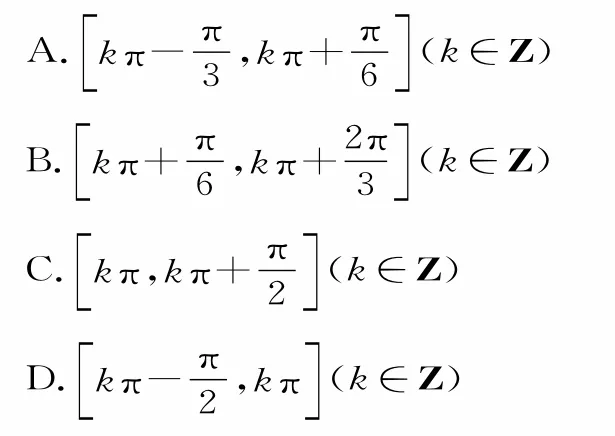
解：f（x）=asin 2x+bcos 2x=sin（2x+φ），其中φ由所確定。

跟蹤訓練3：已知則=（ ）。

提示：因為所以應選B。

題型四：三角函數的圖像問題

高考對三角函數的圖像與性質的應用問題的考查主要有五種命題角度：圖像變換與函數性質；恒等變換與函數性質；三角函數圖像與性質；三角函數性質與平面向量；三角函數性質與解三角形。

例4若將函數f（x）=sin（2x+φ）+的圖像向左平移個單位長度，平移后的圖像關于點對稱，則 函 數g（x）=cos（x+φ）在上的最小值是（ ）。

解：因為f（x）=sin（2x+φ）+所以將函數f（x）的圖像向左平移個單位長度后，得到函數的解析式為又該圖像關于點對稱，其對稱中心在函數圖像上，所以解得，即φ=kπ-由0＜φ＜π，可得，這時

跟蹤訓練4：函數的圖像可由函數的圖像至少向右平移____個單位長度得到。

提示：因為所以把的圖像至少向右平移個單位長度可得到函數y的圖像。

題型五：三角函數的化簡問題

三角函數的化簡是三角函數的基本題型之一，一般涉及誘導公式、兩角和與差的公式、二倍角公式以及三角函數的恒等變形。三角函數的化簡要遵循“三看”原則：一看角，這是最重要的一環，通過看角之間的差別與聯系，把角進行合理的拆分，從而正確使用公式；二看函數名稱，看函數名稱之間的差異，從而確定使用的公式，常見的有“切化弦”等；三看結構特征，分析結構特征，可以幫助找到變形的方向，如“遇到分式要通分”等。

例5化簡

解

跟蹤訓練5：化簡

提示

題型六：非特殊角的求值問題

三角函數給角求值問題的解題策略：一般所給角都是非特殊角，要觀察所給角與特殊角間的關系，利用三角變換轉化為求特殊角的三角函數問題。此類問題也常通過代數變形（如正負項相消、分子分母相約等）的方式來求值。

例 6的值是____。

解

跟蹤訓練6：4 cos 50°-tan 40°=____。

提示：原式

題型七：給值求值問題

三角函數的給值求值問題的解題步驟：先化簡所求式子或所給條件，再觀察已知條件與所求式子之間的聯系，最后將已知條件代入所求式子，化簡求值。

例7已知實數若sin[2（α+γ）]=3 sin 2β，則m=（ ）。

解：設A=α+β+γ，B=α-β+γ，則2（α+γ）=A+B，2β=A-B。

因為sin[2（α+γ）]=3 sin2β，所以sin（A+B）=3 sin（A-B），即sinAcosB+cosAsinB=3（sinAcosB-cosAsinB），2 cosAsinB=sinAcosB，由此可得tanA=2 tanB。

跟蹤訓練7：已知則

提示

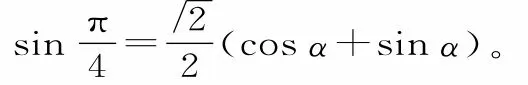
題型八：三角函數的給值求角問題

三角函數給值求角問題的解題策略：通過先求角的某個三角函數值來求角，在選取函數時，遵循以下原則：①已知正切函數值，選正切函數。②已知正、余弦函數值，選正弦或余弦函數，若角的范圍是，選正弦或余弦函數皆可；若角的范圍是（0，π），選余弦函數較好；若角的范圍為，選正弦函數較好。

例8已知且，求β的值。

解：由，可得所以由可得故cosβ=cos[α-（α-β）]=cosαcos（α-β）

跟蹤訓練8：已知銳角α，β滿足sinα=，則α+β等于（ ）。

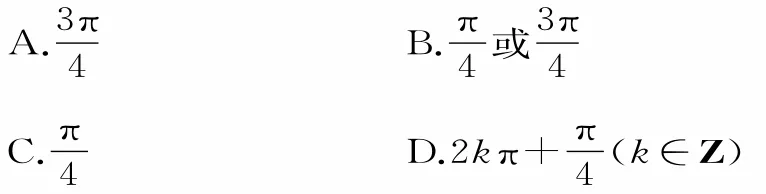
提示：由且α，β為銳角，可知

故cos（α+β）=cosαcosβ-sinαsinβ=因為0＜α+β＜π，所以應選C。

題型九：三角函數的性質問題

求解三角函數的奇偶性、周期性、單調性、最值等問題時，一般先要進行三角恒等變換，把三角函數式化為一個角的一種三角函數，再根據函數奇偶性的概念、三角函數奇偶性的規律、三角函數的周期公式求解。

例9已 知 函 數f（x）=sin2ω x+的最小正周期為 π，則f（x）在 區 間上的值域為（ ）。

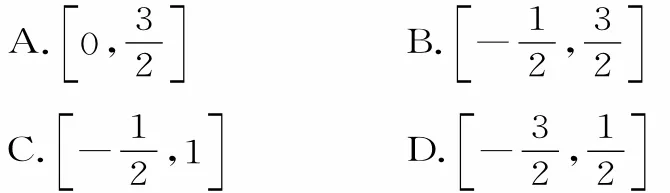
解：函數因為，所以ω=1，這時函數

跟蹤訓練9：已知函數的最大值為A，若存在實數x1，x2，使得對任意實數x總有f（x1）≤f（x）≤f（x2）成立，則A|x1-x2|的最小值為（ ）。

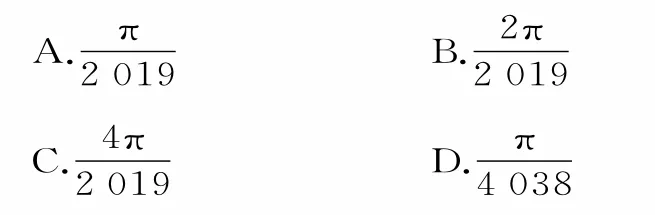
提示：因為sin 2019x+cos 2019x=，所以函數f（x）的最大值為A=2。

由題意可得|x1-x2|的最小值為所以A|x1-x2|的最小值為應選B。

題型十：三角函數與平面向量的交匯問題

平面向量與三角函數在“角”之間存在著密切的聯系。如果在平面向量與三角函數的交匯處設計考題，其形式多樣，解法靈活，極富思維性和挑戰性。對于這類問題，若根據所給的三角式的結構及向量間的相互關系進行處理，可使解題過程得到簡化，從而可以提高解題的速度。

例10已知向量，函數f（x）=m·n。

（1）求函數f（x）的最小正周期。

解：（1）由題意可得函數，所以函數f（x）的

跟蹤訓練10：設向量a=（cosα，-1），b=（2，sinα），若a⊥b，則（ ）。

提示：由a⊥b，可得a·b=2 cosαsinα=0，所以tanα=2。