例析三角恒等變換中的角變換

■王麗娜

三角恒等變換問題中，常見的題型有給值求角和給角求值，解答這類問題的關鍵是角的變換，也就是構造角的問題。角變換的核心是利用已知角構造出所求角，然后利用和差角公式展開求解。下面舉例分析，供大家參考。

解：因為，所以

評析：題中所給角不是特殊角，不能用和差角公式展開求解。如果將所求角進行變換，即則問題就變得簡單易解了。

例2已知則tan（β-α）的值為____。

解：β-α=（α+β）-2α。

故tan（β-α）=tan[ （α+β）-2α]

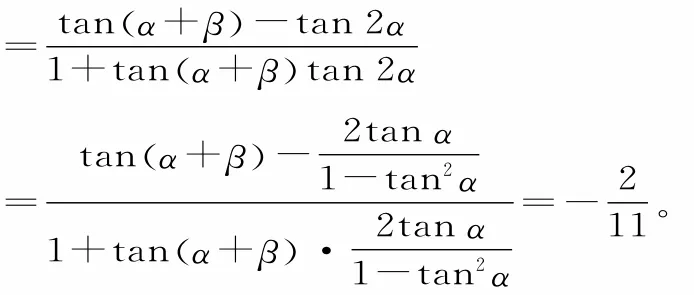
評析：把所求角進行變換，即β-α=（α+β）-2α，再借助正切的差角公式和二倍角公式求解。

例3已知，且0＜x＜，則的值為（ ）。

解：因為，所以原式=應選A。

評析：把所求角進行變換，即2x=再利用誘導公式和二倍角公式求解。

例4已知且求sin（α+β）的值。

解：由，可得由可 得

評析：解答本題的關鍵還是角的變換，即解題時，要注意角的取值范圍對三角函數值的影響。