揭秘三角變換中角變換常見的幾種策略

■郭明龍

三角變換通常是指角變換和函數名稱變換，而其中的角變換是同學們學習的重難點，雖然角的變換錯綜復雜，但是卻有規律可循。下面介紹幾種三角變換中角變換的策略，以供同學們參考。

一、化結論角為條件角的和或差

例1已知，則cos 2α的值為（ ）。

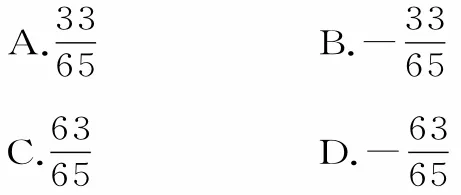
分析：由條件求值時，要仔細觀察條件與結論中的角的差異，設法尋找角之間的關系。因為2α=（α+β）+（α-β），所以結論中的角可用條件中的角表示，從而求出三角函數的值。

解：因為β＜α，所以α-β＞0。又因為所以所以，所以sin（α-β）＞0，故sin（α-

所以cos2α=cos[（α+β）+（α-β）]=cos（α+β）cos（α-β）-sin（α+β）sin（α-β）=應選B。

點評

常見的角變換有α=（α+β）-β，β=（α+β）-α，2α=（α+β）+（α-β），2β=（α+β）-（α-β），等。

跟蹤練習1：若則的值為（ ）。

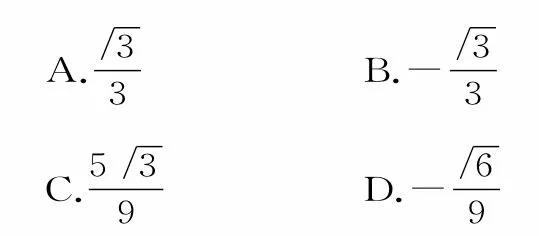
提示：

二、化條件角為結論角的和或差

例2已知3 sinβ=sin（2α+β），求證：tan（α+β）=2 tanα。

分析：觀察條件等式和結論等式中的角的種類差異，我們發現可以采用角的變換，即β=（α+β）-α，2α+β=（α+β）+α來解題，所以本題的證明可從角的變換入手。

證明：因為3 sinβ=sin（2α+β），所以3 sin[（α+β）-α]=sin[（α+β）+α]，即3 sin（α+β）cosα-3 cos（α+β）sinα=sin（α+β）cosα+cos（α+β）sinα。所以2 sin（α+β）cosα=4 cos（α+β）sinα，即tan（α+β）=2 tanα。

點評

通過觀察條件和結論中角的關系，可以變換條件中的角，將結論中的角表示為條件中的角。

跟蹤練習2：已知2 sinα=sin（α+β），求證

證明：因為α=（α+β）-β，所以sinα=sin[（α+β）-β]=sin（α+β）cosβ-cos（α+β）·sinβ。所以2 sin（α+β）cosβ-2 cos（α+β）·sinβ=sin（α+β），兩邊同除以cos（α+β），得2 tan（α+β）cosβ-2 sinβ=tan（α+β）。所以

三、化非特殊角為特殊角

例3求函數cos（x+55°）的最大值。

分析：觀察函數式中的角的種類差異，我們發現可以利用角的變換，即利用x+55°=（x+10°）+45°來解題。

解：因為sin（x+55°）。所以函數cos（x+55°）的最大值為1。

點評

通過求角的和或差能呈現出特殊角，找到互余、互補、半角或倍角的關系，使已知角與待求角之間發生聯系，選擇相應的三角公式進行變形，可順利解答這類問題。

跟蹤練習3：計算的值。

提示：因為sin47°=sin（30°+17°）=sin 30°cos17°+cos30°sin17°，所以原式=

四、消去無關角

例4已知sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，則cos（α-β）的值為（ ）。

分析：因為要求的結果與γ無關，所以要想辦法把γ消去。

解：把條件中的兩個等式變形為：

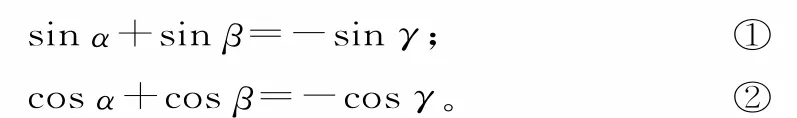
由①2+②2得2+2（sinαsinβ+cosα·cosβ）=1，所以應選A。

點評

對于已知sinα±sinβ=m，cosα±cosβ=n，其中m，n為常數，求α±β的三角函數值的問題，常常可以用平方相加的方法來解決。

跟蹤練習4：已知sinα+cosβ+sinγ=0，cosα+sinβ+cosγ=0，則sin（α+β）的值為（ ）。

提示：把條件中的兩個等式變形為：

由①2+②2得2+2（sinαcosβ+cosα·sinβ）=1，所以應選B。

五、縮小角的范圍

例5已知，且α，β∈（0，π），則2α-β的值為（ ）。

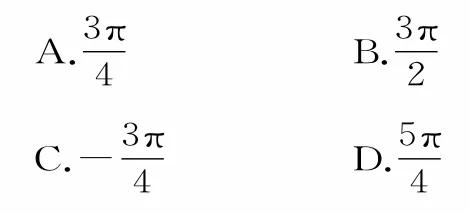
分析：由給定的三角函數值求角時，一般先選擇一個適當的三角函數，根據題設確定所求角的范圍，再利用三角函數的單調性求出角的范圍。

解：tan（2α-β）=tan[2（α-β）+β]=因為tan2（α-β）=，所以：

tanα=tan[（α-β）+β]=。又因為α，β∈（0，π），所以，即由tanβ=，且α，β∈（0，π），可知所以：

點評

對于已知兩角的范圍，求它們倍角的和或差的三角函數值時，必須利用已知條件使每個角的范圍盡可能地縮小，這樣才不會產生增根。所以確定角的范圍是解題的關鍵，同時一定要使所選的三角函數在此范圍內是單調的。

跟蹤練習5：已知α，β為三角形的兩個內角，則β=____。

提示：因為0＜α＜所以，故又所以或由，知，所以cos（α+β）=

所以cosβ=cos[（α+β）-α]=cos（α+因為0＜β＜π，所以