基于機器學習的馬尾松毛蟲發生面積預測模型

龐永華，冀小菊

(1.河南省上蔡縣森林病蟲害防治檢疫站，河南 上蔡 463800；2.河南省上蔡縣林業技術推廣站，河南 上蔡 463800)

馬尾松毛蟲(Dendrolimuspunctatus)屬鱗翅目(Lepidoptera)、枯葉蛾科(Lasiocampidae)，為我國南方18個省區的重要害蟲，主要危害馬尾松，是我國常發性森林害蟲[1]。該害以幼蟲取食松針，暴發成災時，數日內可將大面積連片的松林針葉吃光，遠看焦黃、發黑，如同火燒一樣，嚴重影響樹木生長，造成松樹枯死[2]。因此，加強馬尾松毛蟲發生趨勢預測預報研究，在其大發生之前進行控制，可以把對松林的危害損失降低到最小程度。

馬尾松毛蟲的發生及其種群數量變化與氣象因子和林分結構有關[2-4]，若不考慮林分因素，馬尾松毛蟲的發生量和發生面積主要與氣象因子有關。為此，很多學者利用氣象因子，通過線性回歸[5]、判別分析[6]、馬爾科夫鏈[7]等方法對馬尾松毛蟲的發生量和發生面積進行了預測，這些方法多屬于線性預測方法，實際上害蟲的發生與氣象因子的關系為復雜的非線性關系[8,9]，故探討預測精度更高的非線性預測方法非常重要。

近年來，很多學者利用機器學習模型建立了害蟲發生量與氣候因子的非線性模型，預測精度比傳統的線性預測模型高[10-17]。對于馬尾松毛蟲發生面積的預測，很多學者運用人工神經網絡模型進行預測，預測精度優于線性回歸模型[14-18]。但是運用深度學習、隨機森林、支持向量機等機器學習模型對馬尾松毛蟲的發生面積的預測并選擇最優模型相關報道較少。

1 材料與方法

1.1 數據來源

本研究采用的20組馬尾松毛蟲發生面積數據和氣象數據來自陳繪畫等學者的研究[2]，其中馬尾松毛蟲發生面積數據資料來自浙江省仙居縣森林病蟲防治站，氣象資料來自浙江省仙居縣氣象局。

1.2 預報因子的選擇

對馬尾松毛蟲發生面積的8個氣象預測因子：當年2月下旬平均氣溫(x1)、當年3月上旬平均氣溫(x2)、當年2月中旬相對濕度(x3)、上年10月中旬降水量(x4)、上年9月中旬日照時數(x5)、上年6月上旬最低氣溫(x6)、上年8月中旬最低氣溫(x7)、上年12月中旬最低氣溫(x8)進行逐步線性回歸分析[2]，最終選擇3個進入逐步回歸模型的氣象因子：x2、x5和x8作為線性模型、隨機森林、支持向量機和深度學習模型建模的自變量，預測馬尾松毛蟲的發生面積。用前18個年份的數據作為訓練集，構建模型，后兩年的數據作為測試集，驗證模型的精度。

1.3 選用的模型預測方法

1.3.1 多元線性回歸 多元線性回歸是利用氣象因子預測蟲害的常用方法[3,5]。采用R軟件中的lm函數建立當年3月上旬平均氣溫(x2)、上年9月中旬日照時數(x5)和上年12月中旬最低氣溫(x8)3個氣象因子與馬尾松毛蟲發生面積(y)的多元回歸線性模型。

1.3.2 隨機森林模型 隨機森林(random forest)模型是一種基于分類樹的機器學習算法[8-10]，即在變量(列)的使用和數據(行)的使用上進行隨機化，生成很多分類樹，再總分分類樹的結果構建模型。采用R軟件中的randomForest程序包構建隨機森林模型，ntree=200。

1.3.3 支持向量機模型 支持向量機(support vector machine，SVM)的基本思想是通過非線性映射將數據映射到高維空間特征空間，然后在該空間進行線性回歸，讓所有樣本點的總偏差達到最小，進而提高模型的預測能力[8-9,10,12]，在諸多機器學習模型中因其準確高效而備受關注。采用R軟件中的e1071軟件包的SVM構建支持向量機模型。

1.3.4 深度學習模型 深度學習(deep learning)是在神經網絡模型基礎上建立的預測精度更高的機器學習模型之一，該模型可以逼近任意的非線性函數，能夠處理系統內難以解析的規律型，具有良好的泛化能力[19]。采用R軟件中的h2o程序包建立深度學習模型，設置隱含層數為3，各層的節點數分別為10、8和8，，訓練次數為500次，訓練誤差為1×10-6。

1.4 模型評價方法

1.4.1 均方根誤差 用均方根誤差(Root mean square error, RMSE)作為指標來衡量多元線性回歸、隨機森林、支持向量機和人工神經網絡4個模型的性能[11]。RMSE的計算公式如下：

(1)

公式(1)中：Xa,i為實測值，Xb,i為模型預測值，n為預測樣本數。

1.4.2 預測準確率 預測準確率(PA, %)[17,18]的計算公式如下，式中的參數含義如公式(1)所示。

(2)

2 結果與分析

2.1 模型擬合

選擇18組數據，分別采用多元線性回歸、隨機森林、支持向量機和深度學習構建模型，通過模型的決定系數、RMSE和殘差來比較所建的4個模型的性能。由圖1可知，4個模型的決定系數R2的大小順序為深度學習(0.9901)>支持向量機(0.9617)>隨機森林(0.9584)>多元線性回歸(0.8861)；均方根誤差RSME的大小順序為多元線性回歸(0.5493)>隨機森林(0.4269)>支持向量機(0.3275)> 深度學習(0.00453)。說明多元線性回歸模型的擬合效果最差，3個機器學習模型的擬合效果均優于多元線性模型，其中深度學習模型的擬合效果最好，其次為支持向量機模型。

圖2為4個模型預測值與實際值相比較的誤差，與3個機器學習模型相比，多元線性回歸模型的預測值誤差異常點較多；其次為隨機森林模型；支持向量機模型預測值誤差異常點較少，精度較高；深度學習模型預測值與實測值差異很小，誤差點幾乎均位于零值線上，說明深度學習模型的擬合精度最高。

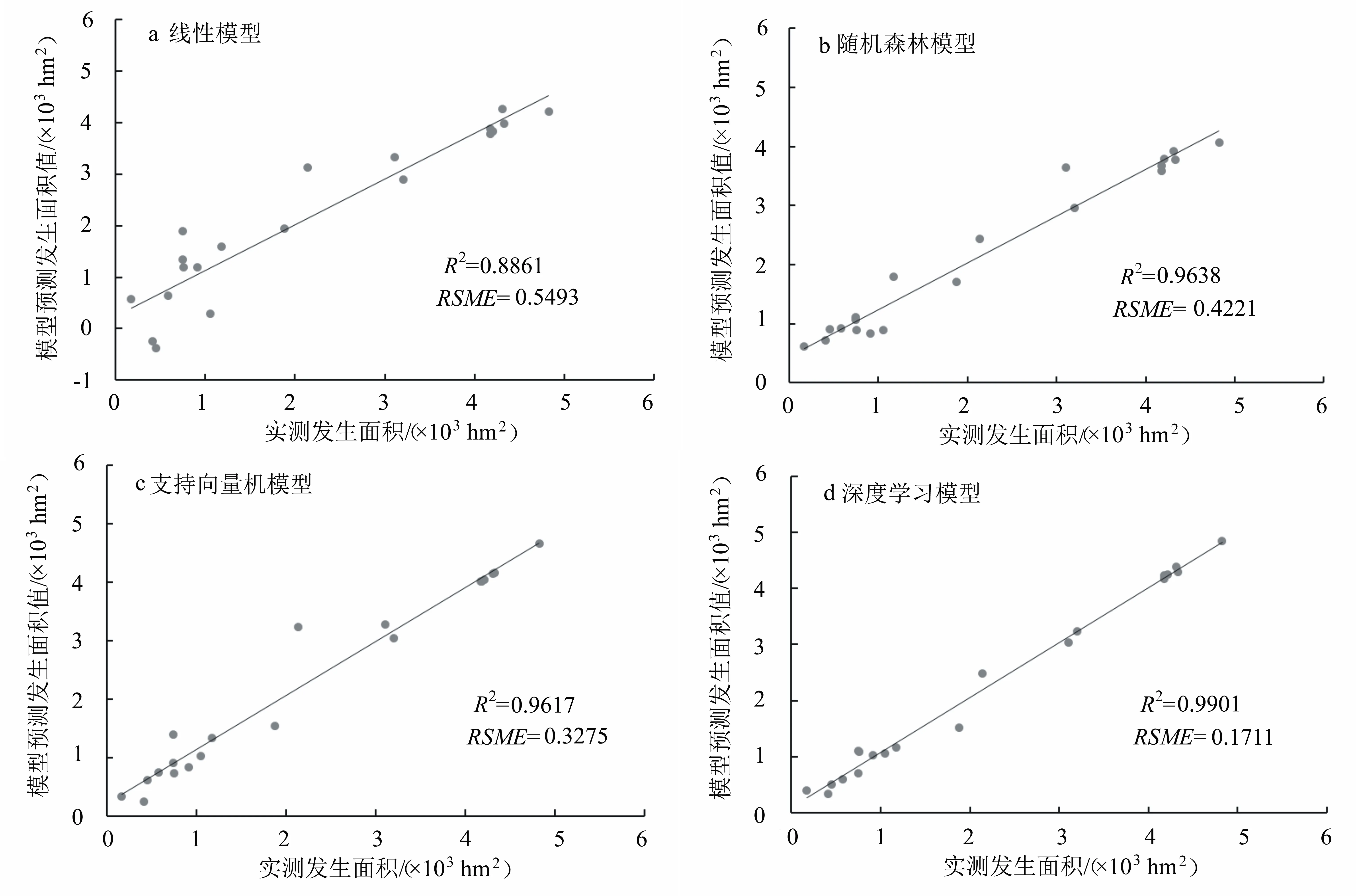
圖1 預測馬尾松毛蟲發生面積

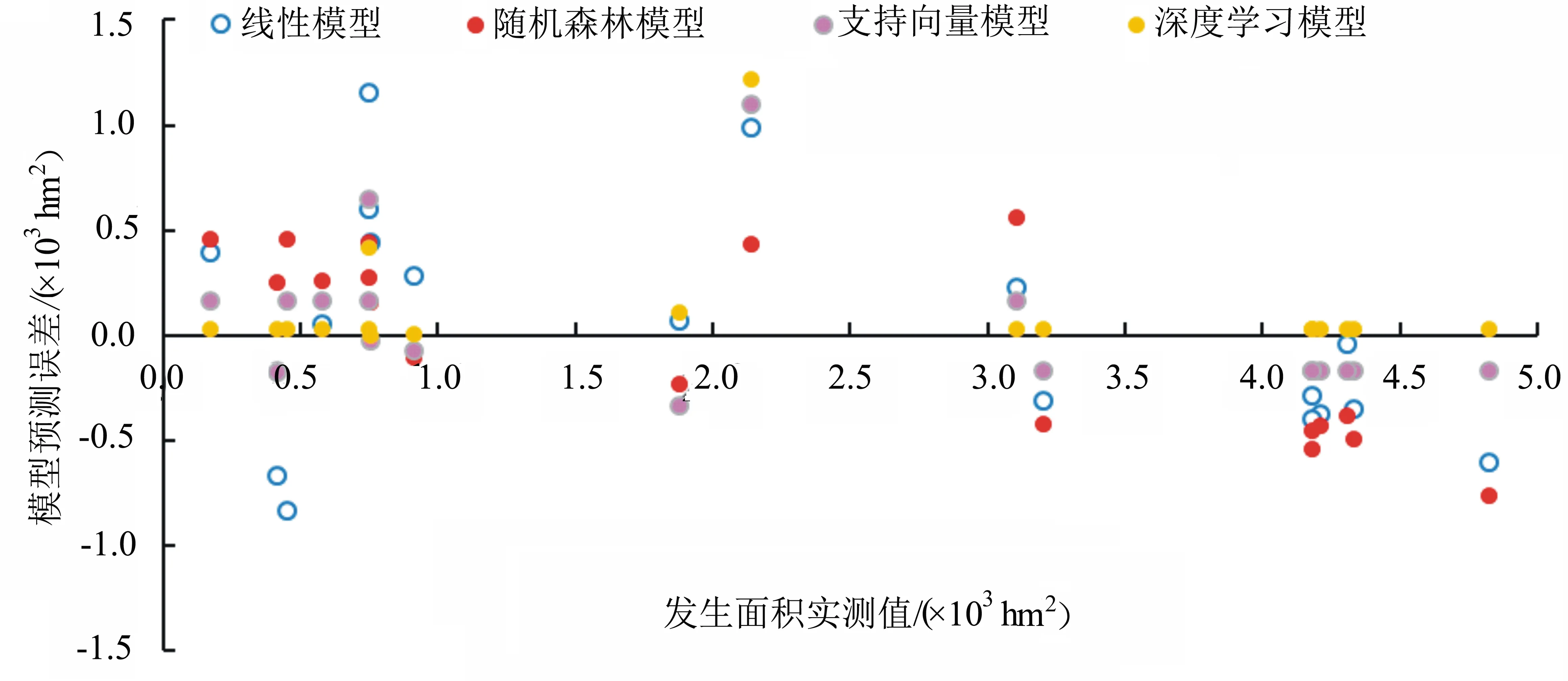
圖2 4種模型預測馬尾松毛蟲發生面積誤差比較

2.2 模型預測與驗證評估

把預留的2001和2002年數據代入4個模型中，對4個模型的預測精度進行驗證比較(表1)。由表1可知，多元線性回歸模型對2001和2002年馬尾松毛蟲發生面積的預測值誤差均較大，兩年的平均預測準確率最低，僅為45.61%；深度學習模型預測值誤差最小，兩年馬尾松毛蟲發生面積平均預測準確率最高，為99.27%；其次為支持向量機模型，平均預測準確率為92.13%。

表1 4種機器學習模型對馬尾松毛蟲發生面積的預測效果比較

3 結論與討論

本研究表明，傳統的多元線性模型對馬尾松毛蟲發生面積的預測擬合度和預測誤差較大，3種機器學習模型對馬尾松毛蟲發生面積的預測效果均優于傳統的多元線性模型，這與很多學者的研究結果一致[2, 11, 14-17]。由此可見，雖然所選擇的預報因子一樣, 但由于氣象因子與森林害蟲的關系并非單純的線性關系[2, 11, 17]，深度學習、支持向量機和隨機森林模型利用了各氣象因子相互之間及其與害蟲發生面積之間的相互關系，進行深度學習訓練[11, 17]，無論擬合精度和預測效果均比傳統的線性回歸模型好。

在3種機器學習模型中，深度學習對馬尾松毛蟲發生面積的預測最為穩健，擬合決定系數和預測準確率最高(R2=0.9901，PA=99.27%)，RSME最低，僅為0.1711。證明深度學習模型用于馬尾松毛蟲發生面積預測更為科學可靠，原因是深度學習具有較強的自適應、抗干擾和容錯性等能力，個別學習樣本的分量偏差對網絡的學習效果影響較小，因此模型的穩定性較好[19]。很多學者利用神經網絡模型進行馬尾松毛蟲發生量和發生面積預測，也取得了滿意的預測效果[14-16]。其次，支持向量機模型預測效果也較好(R2=0.9617，RSME=0.3275，PA=92.13%)，隨機森林模型相對較差。支持向量機與隨機森林相比，支持向量機更適合處理小樣本問題[8, 9, 17-18]。本研究的樣本量較小，可能是造成隨機森林模型預測誤差較大的原因。建議在今后的研究中，加強對馬尾松毛蟲長時間序列發生面積、發生量及其氣象因子的觀測，增大樣本量，深入開展機器學習模型在馬尾松毛蟲發生面積和發生量預測預報中應用的研究，提高馬尾松毛蟲的預測預報準確率。