基于學習者視角下的初中數學“自由課堂”初探

祁帥

[摘 ?要] 開放課堂、自主課堂、生本課堂、民主課堂……在新課改背景下，各種新型課堂應運而生，這些課堂雖然教學形式略有不同，但是教學理念卻是一致的，即在課堂教學中給學生更多的權利與自由，讓學生主動學習、自主獲取知識.

[關鍵詞] 課堂;思維;自由;初中數學

自由課堂有利于提高學生的創造能力，也是社會發展所必需的，但是在教學實踐中卻經常會遇到一些問題：學生在開放的課堂上很容易因“跑偏”而脫離教學內容，課堂過于開放有時候會導致無法完成教學任務;自由課堂導致部分學生“過分自由”而影響課堂教學秩序等. 筆者也曾經被這些問題所困擾，在請教了前輩與同仁的基礎上，經過多次反思及總結，筆者對自由課堂有了一些新的認識：秩序是課堂教學有效進行的必要保障，“自由”并非“散漫”，自由與約束是相對的也是共存的，自由課堂需要教師充分準備、嚴格把控、收放自如，方能體現自由課堂的實質. 下文擬通過常態課“平面直角坐標系”的教學片段來談談筆者對自由課堂的認識：

情境引入：敞開發言之大門，期許平面直角坐標系

？搖？搖新授課常常由引入開始，引入環節的目的是吸引學生的注意，激發學生的興趣. 在以學生為主體的教學中，“敞開大門”的方式是值得推薦的，即以一個大問題讓學生自己發揮想象、提出探究欲望，以形成對本節課的期待.

導入語：在我校今年舉辦的運動會開幕式上，有一個節目非常震撼，就是全校同學站成方陣根據口令舉出手中不同顏色的旗子顯示倒計時，當時的航拍景象非常壯觀，大家一定記憶猶新吧？

（學生均點頭表示肯定，還有學生想發言，躍躍欲試的）

師：大家還記得這個節目是怎么排練的嗎？如何保證大家有序變換手中的顏色讓大字準確出現呢？

生1：老師給了我們每個同學一個坐標，由兩個數字組成，然后老師根據每個同學的坐標讓我們記住自己的舉旗步驟，這樣排練幾次就熟練了.

師：回答得真好，你一定是在參加活動的時候就不斷動腦筋的. 那么，老師所說的這個由兩個數字組成的“坐標”表示的是什么呢？

生1：表示我們每個同學的位置.

師：非常棒，你的領悟能力很強！今天我們就來深入了解一下這個“坐標”.

教師板書課題“平面直角坐標系”.

師：大家覺得我們這節課要學習哪些知識呢？你又想通過本節課的學習學到什么呢？

生2：我想知道什么是平面直角坐標系？平面直角坐標系在數學中有什么作用？

生3：我想知道為什么要加“平面”兩個字？難道還有“非平面直角坐標系”嗎？另外，“直角”是跟直角三角形有關嗎？

生4：我想知道除了開幕式上的倒計時節目，平面直角坐標系在生活中有什么作用？

生5：我想厘清平面直角坐標系和數軸有什么關系？

……

教學分析 教師在引入環節的任務是把學生引進本節課的知識庫中，學生想學什么、怎么學，可以由他自己決定，因此教師揭示課題之后可以讓學生自己提出問題，描述對本節課的期待. 有些問題看似脫離了教學內容，但也正是這些問題才是最適合學生、最能激發學生的學習熱情. 由運動會開幕式的“舉旗”航拍引入，既直奔主題又拉近與學生的距離.

探究新知：架起遷移之橋梁，認識平面直角坐標系

數學學科相對于其他學科來講更為“樸素”，在教與學中沒有太多的“花樣”，教學追求的是從不斷鉆研中學會學習、發展思維，從而領悟到數學的獨特魅力. 數學新授課應在教師的引領下進行，這樣才能保證學生的思維向正確的方向發展，學會正確思考問題的路徑，所以在探究新知的環節應在教師的把控之下有序進行.

問題1：看電影的時候我們總能根據電影票找到自己的位置，那么細心的你有沒有觀察過你是根據電影票上的什么來確定自己的位置的呢？

問題2：如果老師想知道你在班級中的具體位置，你能用最準確的位置描述出自己所處的位置嗎？

問題3：如果我們約定“列數在前，行數在后”，用兩個數來表示你好朋友的位置，你能不能表示呢？

（完成方式：學生獨立思考后全班交流展示）

（學生在教師的引導下認識“有序數對”，理解它的含義）

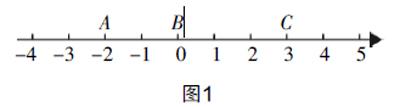
師：我們知道數軸上的點與實數是一一對應的，數軸上的每個點都對應一個實數，反過來，每個實數都可以在數軸上找到對應的位置. 如圖1，點A在數軸上所表示的數是-2，點B是原點，表示0，反過來，在數軸上表示3的點就是點C.

問題4：想象一下，如果我們在平面內畫一條可以無限延長的數軸，那么我們能不能用數軸來確定平面內的任意一個點呢？你的理由是什么？

（完成方式：學生小組討論，組內統一意見后小組代表全班展示）

組1：我們小組覺得不能，無論數軸畫在什么位置，都會有很多點不在數軸上，數軸只能表示數軸上的點.

師：你回答得很堅定，看來你們是對數軸的理解非常透徹了，那我們有什么辦法來確定平面內的任意一點呢？

組2：我覺得數軸好比我們剛才確定自己在班級的座位時的“列”，只知道列數顯然不能確定一個位置，還需要知道行數，所以我們小組的意見是再畫一條縱向的坐標，就能確定了.

（師生共同建立直角坐標系模型，概括平面直角坐標系的構成要素、介紹相關概念及平面直角坐標系的畫法）

問題5：我們知道數軸上的點與實數是一一對應的關系，那么平面直角坐標系上的點與有序實數對是否也是一一對應的關系呢？

（眾生均點頭表示肯定）

問題6：如果我們給定一個有序數對，你如何在平面直角坐標系中準確將這個點表示出來？相反，如果給定一個點，你能準確讀出它的坐標嗎？試著自己建立一個平面直角坐標系完成探究.

（完成方式：由學生獨立完成，學生代表全班展示）

展示片段：

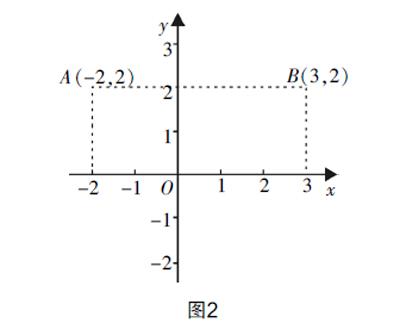
生1：例如，給定一個有序數對（-2，2），如圖2，現在x軸上找到表示-2的點，再在y軸上找到表示2的點，分別過這兩個點作x軸與y軸的垂線，它們的交點A就是表示（-2，2）的點.

生2：如圖2，平面上有一個點B，過這個點分別作x軸與y軸的垂線，分別對應3，2，那么它的坐標就是（3，2）.

教師和學生共同探究由點讀坐標及由坐標找點的方法，并強調橫坐標在前、縱坐標在后的注意點.

問題7：通過剛才的探究，你是否發現了一些特殊的點的坐標特征？比如x軸上的點;另外，同一象限內的點的坐標是否具有哪方面的共同性？

（完成方式：小組討論、組長匯總成果后全班交流展示）

展示片段：

組1：我們小組發現了x軸上的點的縱坐標全部是0，y軸上的點的橫坐標全部是0.

組2：我們小組發現的是x軸正半軸上的點的縱坐標全部是0，橫坐標是正數;x軸負半軸上的點的縱坐標全部是0，橫坐標是負數;y軸正半軸上的點的橫坐標全部是0，縱坐標是正數;y軸負半軸上的點的橫坐標全部是0，縱坐標是負數.

組3：我們總結了每個象限的點的坐標特征，分別是第一象限：（+，+）;第二象限：（-，+）;第三象限：（-，-）;第四象限：（+，-）.

組4：我們還發現了原點的坐標是（0，0），它既在x軸上，又在y軸上.

師生共同梳理歸納，教師完善板書.

探索新知是新授課的中心環節，教師起著主導作用. 在實踐中可以發現該環節的主要權利在不斷發生著轉變，問題由教師提出，探究由學生完成;思路由教師引導，方法由學生總結;概念由學生推導，結論由教師總結. 整個過程學生在教師的引導下主動探究、構建新知，教師時而下放權力，時而又收回，有放有收保證了教學的高效有序進行.

學以致用：鋪設內化之環節，應用平面直角坐標系

學以致用的過程是新知內化的過程，在這一教學環節中實現了兩種遷移：（1）從一維向二維的遷移;（2）從一般向特殊的遷移. 實現教與學的互動，既體現學生的主體地位，又發揮教師的主導作用，使得學與教二者平衡. 在學生掌握基本知識與技能的同時，激勵學生發言，提高學生獨立思考、合作交流和語言表達等終身需要的必備品格和關鍵能力，形成提出問題、分析問題、解決問題的智慧. 這個過程應由學生完成，教師把控好問題的數量及難度，確保每個問題的價值.

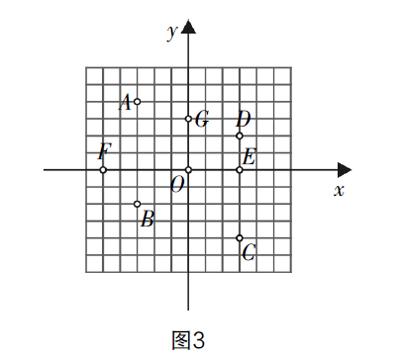
1. 如圖3，寫出圖中點A，D，G，H的坐標，并在圖中標出（-1，4），（3，3），（4，-5）的位置.

2. 在平面直角坐標系中，如果點P的坐標是（-3，2），則點P所在的象限是________.

3. 已知點M到x軸的距離是1，到y軸的距離是2，則點M的坐標是________.

4. 已知點M（m+4，m-2）在平面直角坐標系的y軸上，則點M的坐標為________.

5. 根據你今天所學的知識自己編制一個或兩個用平面直角坐標系來解決的問題，考考你的同桌.

（完成方式：1～4題由學生自主完成后組內互助、糾錯改錯，第5題由學生思考后全班展示）

在1～4題的反饋結果中，除第3題以外其余題目正確率較高，第3題有部分學生考慮不全面，在小組成員的幫助下均可以自行改正消化.

第5題部分成果展示：

（1）已知點A（-4，3），則它位于第幾象限？

（2）如果點P在x軸的負半軸上，且到原點的距離是6，求點P的坐標.

（3）在平面直角坐標系中，點P（2，a2+1）一定位于第______象限.

（4）已知點P（2m+3，4m-7）的橫坐標減縱坐標的差為6，求這個點的坐標.

（5）在平面直角坐標系中有一個長方形，它的其中三個點坐標分別為（4，1），（-3，1），（-3，-1），則它的第四個點坐標是多少？

由學生自己編制的問題可以看出學生能力有差異，每個學生都是在自己的能力范圍內提出問題并解決. 碰撞的火花，使原來刻板模糊的概念變得生動，而正因為學生有不同的想法，才激起了思維，最終形成深刻的理解. 這樣既有利于學困生鞏固基礎，又可以為優等生提供展示的空間和拓展的平臺. 由此可見，該環節的開放式非常必要的，不僅有利于分層教育，也能體現因材施教的原則.

教學中強調圖示語言與符號語言的轉換體會數形結合的數學思想方法，提高學生的數學抽象和直觀想象的素養.

整理反思：搭建回顧之平臺，展望平面直角坐標系

整理反思是每節新授課的必備環節，“小結”并不代表教學的終結，而是知識的凝練與能力的升華. 在這個環節中，學生應該擁有自由發表見解的權利，這樣才有利于反思總結、發展能力.

問題：（1）本節課你收獲了什么？

（2）你在上課初始的疑惑在課上得到解決了嗎？

（3）你在本節課還有什么疑問和不解問題需要老師和同學幫助嗎？

（4）你對下節課的內容有什么期待呢？如果讓你設計教學，你覺得下節課應該學習什么？

（完成方式：學生自由發言、師生共同探討）

展示片段：

生1：本節課我學會了用平面直角坐標系表示平面內的點，體會到了平面直角坐標系在生活中的用處.

生2：我終于知道了為什么是“平面”直角坐標系，因為它只能表示平面內的點，我想知道今后我們是否還要繼續學習空間直角坐標系.

生3：我對練習題3不是太理解，希望老師能仔細講解一下.

生4：我覺得下節課應該學習平面直角坐標系的實際應用.

生5：我在本節課最大的收獲就是借助平面直角坐標系似乎能理解經緯網了.

生6：數形結合思想，表示點位置的方法有所增加：從原來用一維直線上一個數表示點的位置到現在用二維平面上的一個數對來表示點的位置.

在學生的你一言我一語中，教師可以得到最真實的反饋，解答學生疑問的同時對自己的教學進行反思與調整，達到教學相長的效果.

教學有法而無定法，開放課堂不是完全開放，自由課堂并非絕對自由. 學習離不開教師的“教”，也無法剝奪學生的“學”. 在實踐中，唯有不斷反思、不斷調整，才能使教學更有效，課堂更適合學生，有放有收，方能打造有序、自由的新型課堂.