淺談2.3.5的倍數特征教學

葉美叢

(廣東省河源市紫金縣紫城鎮林田小學 廣東 紫金 517400)

2、3、5的倍數教學是在因數和倍數的基礎上進行教學的，是求最大公因數.最小公倍數的重要基礎，從而也是學習約分和通分的必要前提。學生的分數運算是否熟練，取決于約分和通分掌握的是否熟練，而約分和通分是否熟練，在很大程度上取決于能不能很快地根據分子分母的特征看出有什么公因數，能不能很快地求出幾個分數的分母的公倍數。因此，學習掌握2、3、5的倍數特征，具有十分重要的意義。

1.2的倍數教學

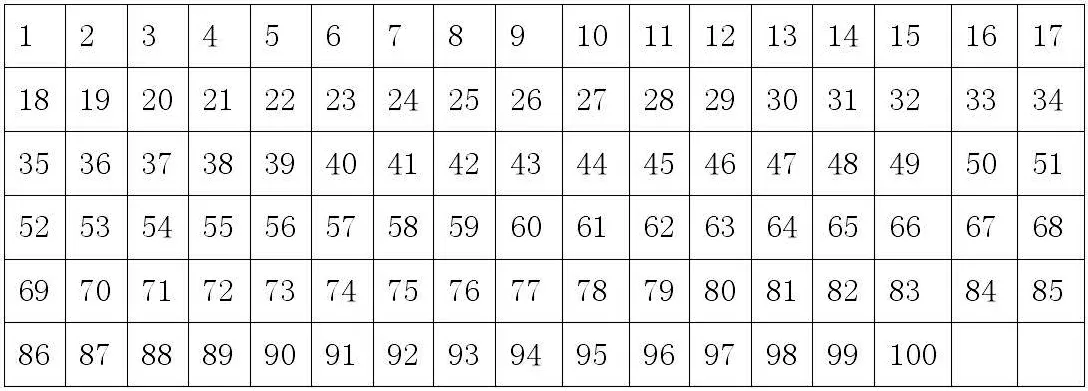
1.1 找倍數。讓學生在百數表內找出2的倍數。

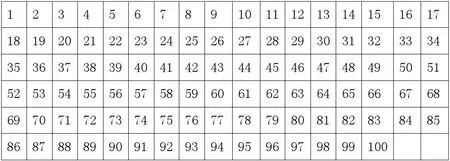
1.2 觀察特征。讓學生觀察找出來的2的倍數特征。

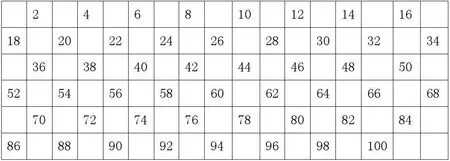
從百數表內2、4、6、8.……96、98、100的個位都是2、4、6、8、0 。

1.3 驗證發現。從百數表內找出來的2的倍數中，個位都是2、4、6、8、0。2=2×1,4=2×2,6=2×3,8=2×4，10=2×5,……90=2×45,92=2×46,94=2×47,96=2×48,98=2×49,100=2×50。

1.4 得出結論。

(1)從百數中找出的2的倍數進行驗證，驗證中得出：個位上是2、4、6、8、0的數就是2的倍數。

(2)用大數繼續驗證。

如：966=2×483 1984=2×992 18966=2×9483 12347898=2×6173949 4568970=2×2284485

通過百數表和大數證明：一個數(大于0)，個位上是2、4、6、8、0的數就是2的倍數。

2.5的倍數教學

2.1 找倍數。讓學生在百數表內找出5的倍數。

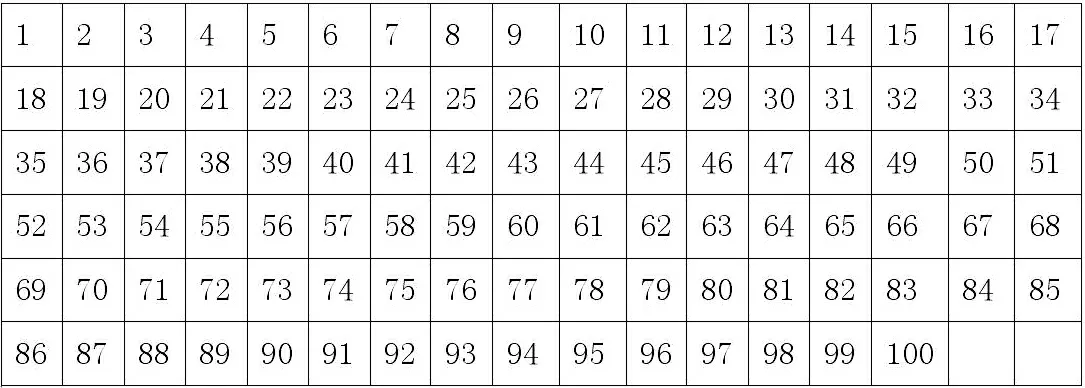
2.2 觀察特征。讓學生觀察找出來的5的倍數特征。

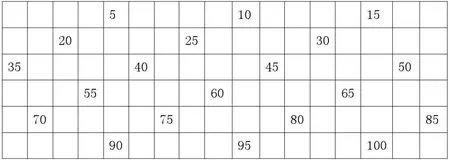
從百數表內5、10、15.……90、95、100的個位都是0或5 。

2.3 驗證發現。從百數表內找出來的5的倍數中，個位都是0或5 。5=5×1,10=5×2,15=3×5,20=4×5，25=5×5,……80=5×16,85=5×17,90=5×18,95=5×19, 100=5×20。

2.4 得出結論。(1)從百數中找出的5的倍數進行驗證，驗證中得出：個位上是0或5的數就是5的倍數。

(2)用大數繼續驗證。

如：105=5×21 1980=5×396 17965=5×3593 12546795=5×2059359 4568970=5×913794。

通過百數表和大數證明：一個數(大于0)，個位上是0或5的數就是5的倍數。

3.3的倍數教學

3.1 找倍數。讓學生在百數表內找出3的倍數。

3.2 觀察特征。讓學生觀察找出來的3的倍數特征。

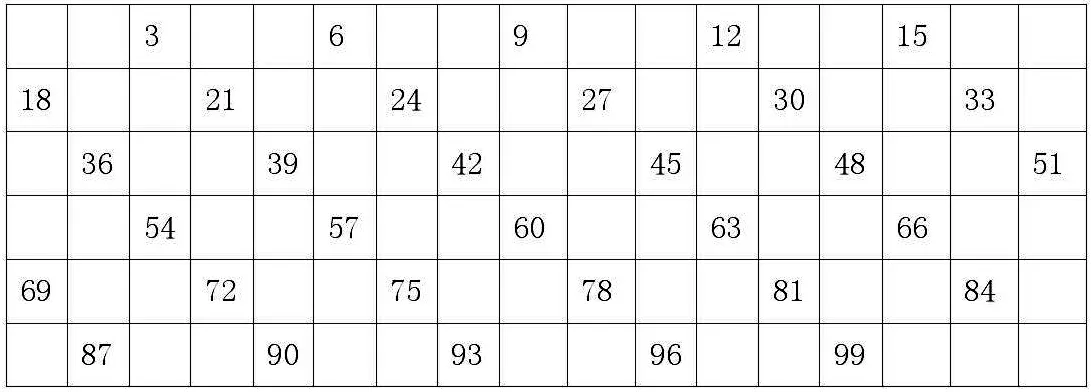
(1)在百數表內，個位是3的不一定是3的倍數。如：3、33、63、93是3的倍數，但13、23、43、53、73、83不是3的倍數。

(2)在百數表內，個位是0或5的不一定是3的倍數。15、30、45、60、75、90是3的倍數，其他不是。

(3)在百數表內，個位是2、4、6、8、0的也不一定是3的倍數……。

(4)在百數表內,3、12、21、30的各個數位上的數字之和是3。6、15、24、33、42、51、60的各個數位上的數字之和是6。9、18、27、36、45、54、63、72、81、90的各個數位上的數字之和是9。39、48、57、66、75、84、93的各個數位上的數字之和是12。69、78、87、96的各個數位上的數字之和是15。99的各個數位上的數字之和是18。

3.3 驗證發現。

從百數表內找出來的3的倍數中各個數位上的數字之和是3、6、9、12、15、18都是3的倍數。

12=1+2=3 15=1+5=6 18=1+8=9 21=2+1=3… …90=9+0=9 93=9+3=12 96=9+6=15 99=9+9=18 。

3.4 得出結論。

(1)從百數中找出的3的倍數進行驗證，驗證中得出：各個數位上的數字之和是3的倍數那這個數就是3的倍數。

(2)用大數繼續驗證。

如：105=1+0+5=6 6是3的倍數。 1980=1+9+8+0=18=1+8=9 9是3的倍數 17965=5×3593 12546795=5×2059359 4568970=5×913794。

通過百數表和大數證明：一個數(大于0)，各個數位上的數字之和是3的倍數那這個數就是3的倍數。

4.小結

通過讓學生在100以內數表中找2、3、5的倍數，觀察它們的特征，經過驗證發現，最后得出結論的教學，讓學生掌握了2、3、5的倍數特征。只有掌握理解了2、3、5的倍數特征，在以后的實踐應用中便會更加清晰地進行求最大公因數、最小公倍數；進行分子分母約分；進行分數通分。實踐證明，要想在以后的求最大公因數、最小公倍數、通分和約分中,立于不敗之地，就必須學習掌握好2、3、5的倍數特征教學。