半漂浮體系斜拉橋粘滯阻尼器布置與參數優化

熊柏林，徐略勤，王 龍，李鐘雄

(重慶交通大學土木工程學院， 重慶 400074)

斜拉橋根據塔、梁、墩結合方式的不同，可分為漂浮、半漂浮、塔梁固結和剛構等4種體系。其中，半漂浮體系受溫度、收縮和徐變的影響較小，基本周期較長，有利于耗能減震，在大跨斜拉橋中應用最廣泛[1]。研究表明，斜拉橋的抗震薄弱環節主要出現在主塔、邊墩、基礎以及支承連接部位[2-3]。主塔與橋墩不同，由于其高度大，軸壓比高，延性較低，且受高階振型的影響，采用延性設計比較困難。此外，主塔抗震薄弱部位常位于塔底，一旦進入塑性，塔頂殘余變位很大，震后難以修復[4]。因此，國內外規范都指出主塔在設計地震作用下應保持彈性[5-6]。在縱橋向，大跨半漂浮體系斜拉橋在強震下梁端容易產生較大的縱向位移，導致伸縮裝置的破壞，引發主梁與相鄰跨引橋的碰撞，造成落梁震害。為了同時實現保持主塔彈性狀態并防止主梁與引橋碰撞的目標，增設粘滯阻尼器是最常見的做法之一[7-8]。在橫橋向，主塔處一般設置抗風支座以制約塔、梁相對運動，邊墩處也往往設置橫向限位裝置，由此導致橋梁橫向剛度很大，邊墩及其基礎因此成為抗震薄弱部位[9]。為了降低邊墩及其基礎的地震反應，可在邊墩處設置橫向粘滯阻尼器。可見，不論從縱橋向還是橫橋向來說，阻尼器布置方式及其參數優化都是應該首要解決的問題。

本文以某新建的半漂浮體系斜拉橋為背景工程，從粘滯阻尼器耗能原理出發，分別就粘滯阻尼器在橋梁縱、橫向減震體系中的作用進行研究。本文在綜合考慮塔、墩、支座等關鍵構件抗震能力的基礎上，探討阻尼器數量和參數的優化，以期為工程建設提供技術參考。

1 粘滯阻尼器耗能原理

粘滯阻尼器一般由活塞、油缸及節流孔組成，利用活塞前后壓力差使油流過節流孔產生阻尼力，如圖1所示。粘滯阻尼器的阻尼力與相對速度的關系可表達為：

(1)

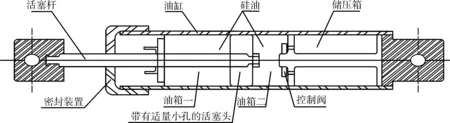
圖1 粘滯阻尼器構造圖

2 工程背景與分析模型

2.1 工程概況

某新建半漂浮體系斜拉橋跨徑布置為(30+75+220+75+30)m，全長430 m，為雙塔雙索面組合梁結構，如圖3所示。H型鋼筋混凝土索塔承臺以上高80 m，塔柱為矩形空心截面。主梁為雙邊“工”字型邊主梁與橋道板的組合斷面，橋寬31.6 m，中心線高3.16 m，混凝土橋道板厚28 cm。兩側邊跨分別設一個輔助墩和過渡墩，其中輔助墩為分離式雙柱，過渡墩為三柱式排架墩。在初步設計中，主塔處布設兩個單向球鋼支座；輔助墩處布設兩個雙向球鋼支座；過渡墩處布設雙向+單向球鋼支座，如圖4所示。

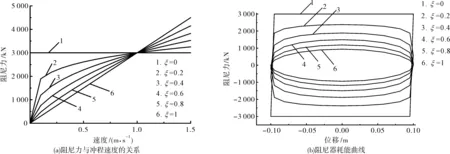
圖2 粘滯阻尼器力學特征

圖3 斜拉橋立面布置圖(單位：m)

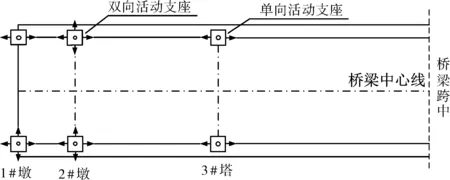
圖4 初步設計的支座布置

2.2 有限元建模

采用SAP2000建立全橋有限元分析模型，如圖5所示。主梁、索塔、輔助墩和過渡墩都用空間梁單元模擬，并考慮受壓構件的二階效應；斜拉索采用只受拉空間桁架單元模擬，按Ernst公式修正垂度效應[1]，并考慮恒載初始內力引起的幾何剛度影響；樁-土共同作用采用6×6集中土彈簧模擬，彈簧剛度系數根據m法計算得到；球鋼支座采用雙線性滯回模型模擬活動方向的滑移摩擦效應，如圖5所示；粘滯阻尼器采用Maxwell計算模型[10]；體系阻尼采用Rayleigh模型，阻尼系數取3%[5]。

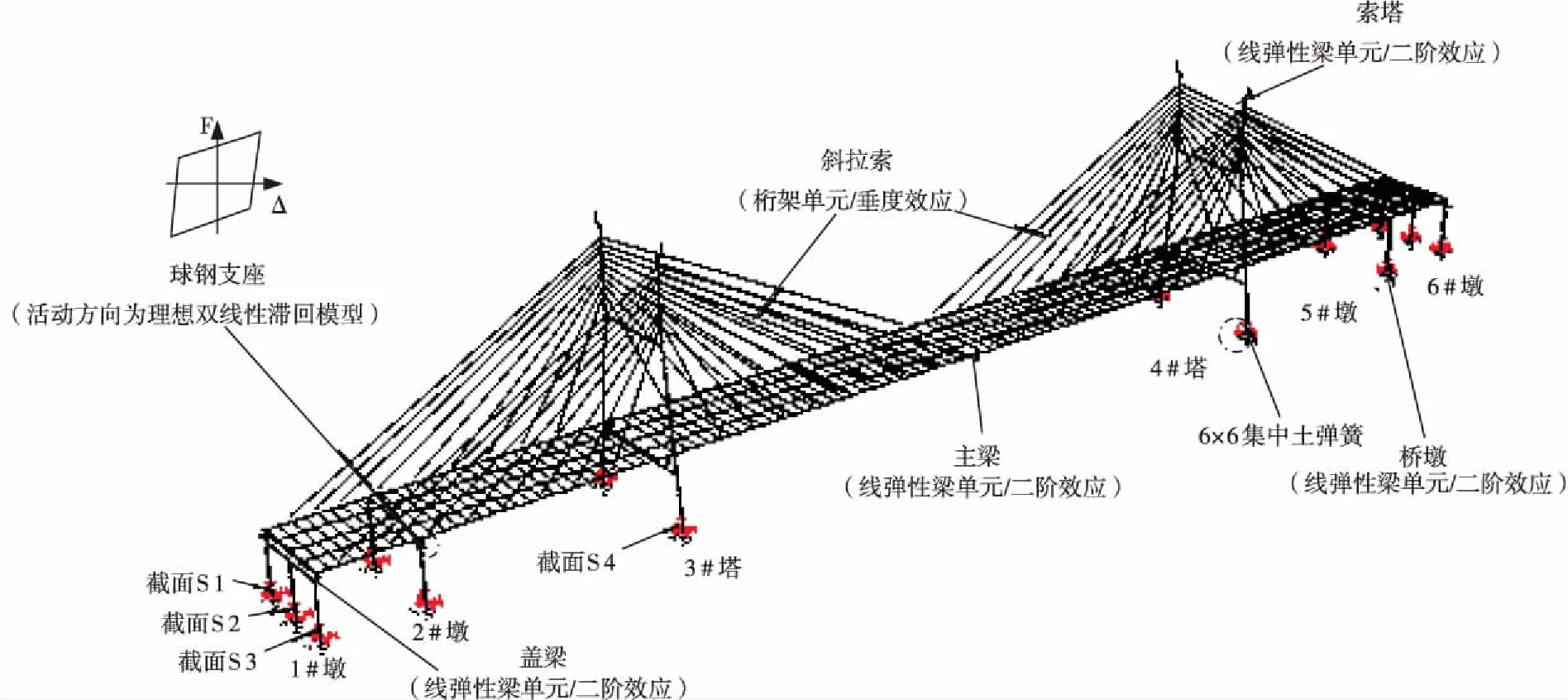
圖5 全橋動力分析模型

2.3 地震動輸入

根據地震安評報告，罕遇地震對應的峰值加速度為0.25g。地震動輸入有兩類，其一是安評提供的3條人工地震波；其二是3條實際地震記錄，并采用小波變換來匹配場地設計反應譜，地震波及匹配情況如圖6所示。在非線性時程分析時，采用縱向+豎向、橫向+豎向的地震輸入方式，其中人工波的豎向地震根據細則[5]采用水平地震折減的方式獲得；實際波的豎向地震直接采用實際豎向地震記錄。后文分析結果的包絡值按6組波的平均值來考慮。

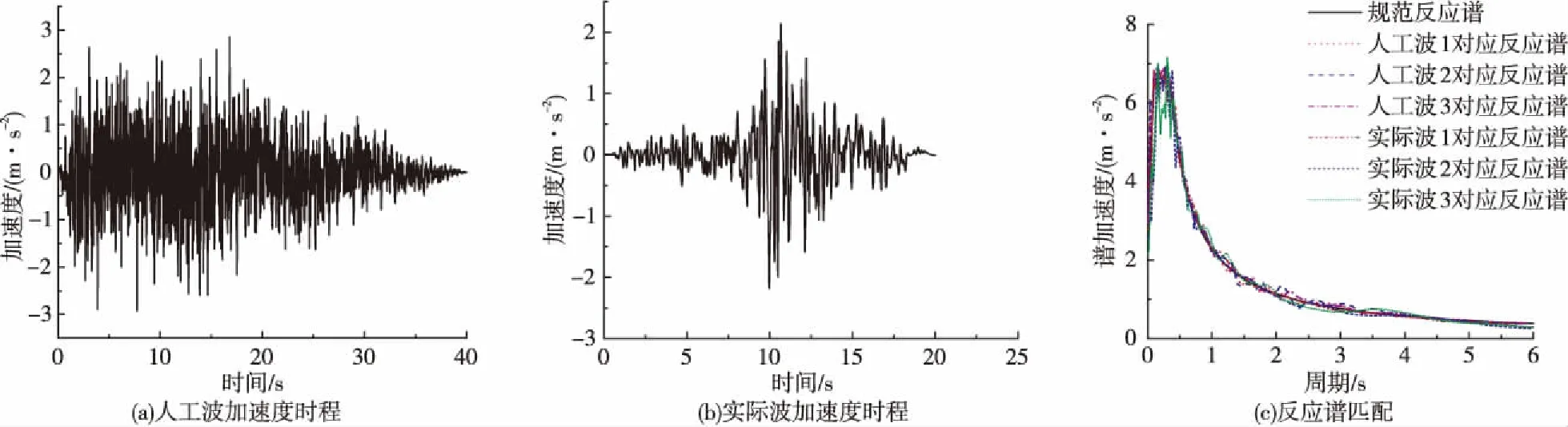
圖6 地震波及匹配情況

3 分析工況

3.1 阻尼器布置方案

按照初步設計，主梁在縱橋向為半漂浮體系，其地震慣性力主要通過拉索傳遞至索塔，輔助墩和過渡墩分擔較小。因此，阻尼器在縱橋向所起的作用是限制主梁位移，防止球鋼支座變形超限，同時降低索塔的地震響應。基于此，阻尼器在縱橋向主要布置在主梁與索塔交接處，考慮造價、外形體積和便于布置等因素，阻尼器性能參數不宜過高，本文分析了3種布置方式，即分別在塔梁交接處布置1個、2個、4個縱向阻尼器，阻尼器參數分別取ξ=0.5和C=5 000 kN/(m/s)ξ。為便于表述，后文將3個工況簡稱為“縱-1阻尼器”、“縱-2阻尼器”、“縱-4阻尼器”。

前期分析表明，按照初步設計，主梁的橫向地震慣性力主要由索塔和過渡墩承擔，輔助墩由于布置雙向支座，參與程度很低，導致兩側過渡墩在橫橋向無法滿足抗震要求。可見，本橋橫向抗震問題更加突出。為了解決過渡墩橫向抗震問題，本文分析了3種布置工況：1)在過渡墩雙向支座的那一側布置阻尼器；2)在過渡墩的兩側都布置阻尼器；3)將初步設計中的單向+雙向支座改為2個雙向支座，然后在兩側都布置阻尼器。阻尼器參數初步取ξ=0.6和C=3 000 kN/(m/s)ξ。為便于表述，后文將3個工況簡稱為“橫-DX+SX單側”“橫-DX+SX雙側”“橫-SX+SX雙側”。

3.2 關鍵構件抗震性能

前期分析對橋梁抗震薄弱環節進行了判別，限于篇幅，本文重點探討過渡墩墩底截面、塔底截面和球鋼支座的抗震能力(輔助墩由于設置雙向支座，抗震富余量較大，未予考慮)。對鋼筋混凝土構件截面進行纖維離散建模，并開展軸力-彎矩-曲率分析，可得到每個截面的初始、等效和極限抗彎能力(分別對應構件的無損傷、可修復損傷和局部破壞3個狀態)，計算方法詳見文獻[2]。由于橋梁在立面布置上對稱，表1列舉了左半側各關鍵構件的抗震能力，后文也以該側(即圖3中的1#墩、2#墩和3#塔)進行分析。

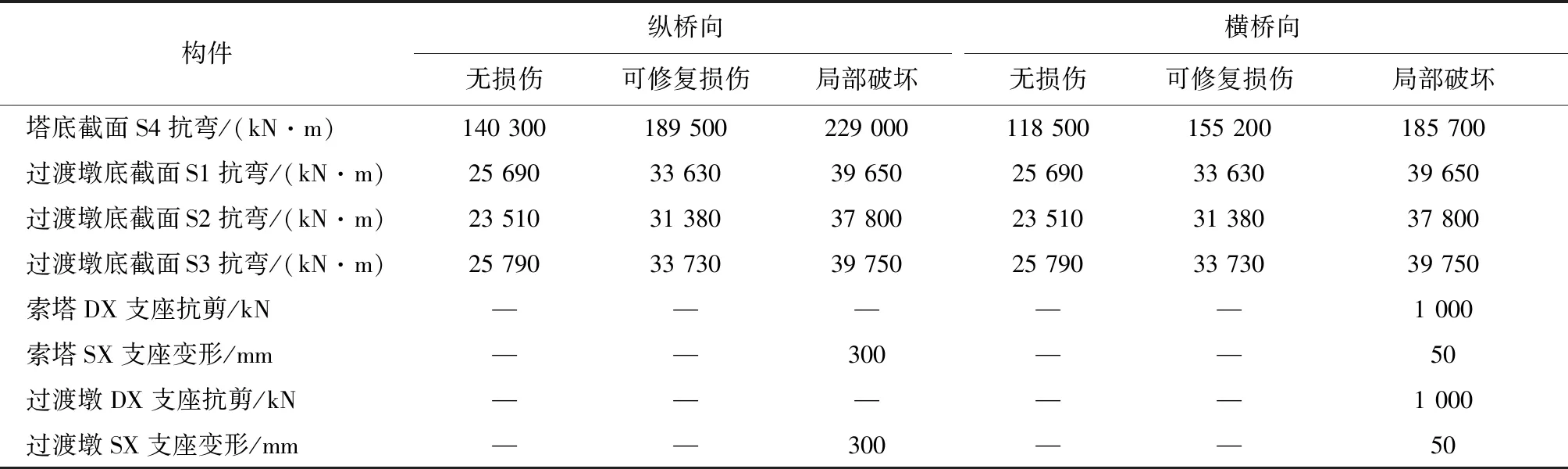
表1 各構件的抗震能力

3.3 減震率

為便于描述阻尼器的減震效果，后文采用減震率進行對比分析，其定義為：

(2)

式中：β為減震率；Enone為無阻尼器時橋梁的地震響應；Edamper為設置阻尼器后橋梁的地震響應。

4 阻尼器布置效果分析

4.1 縱橋向

在縱橋向，本文重點以過渡墩底截面S2和塔底截面S4為內力分析對象，以塔頂、梁端和支座為位移分析對象，計算結果見表2—3。

表2 3種方案地震內力對比

表3 3種方案地震位移對比

由表2可知，不同阻尼器布置方式對索塔內力響應的減震效果非常明顯，但對過渡墩和輔助墩(限于篇幅，輔助墩的結果未列出)的影響很小，幾乎可忽略。隨著阻尼器數量的增加，索塔內力的減震率不斷增大，如塔底S4的彎矩減震率由1個阻尼器的13.0%增大到4個阻尼器的51.1%，而1#墩底S2的彎矩減震率僅由0.9%增至3.2%；剪力的變化規律也類似。結合表1可知，在無阻尼器情況下，索塔將進入“局部破壞”狀態；當設置4個阻尼器時，索塔才能保持“無損傷”狀態。

由表2可知，不同阻尼器布置方式對各構件位移響應的減震效果也非常明顯。無阻尼器時，塔頂位移為374.9 mm，橋塔和過渡墩處的支座變形分別達267.1和325.1 mm(輔助墩上的支座介于這兩者之間，限于篇幅沒有列出)；當設置4個阻尼器時，塔頂位移降至122.4 mm，減震率達67.3%，兩處支座的變形分別降至77.5和129.9 mm，減震率分別達71.0%和60.0%。結合表1可知，不設置阻尼器將導致過渡墩處的支座變形超限，引發支座破壞；設置1個阻尼器或多個阻尼器都可保證全橋支座的抗震安全。

綜合考慮造價和抗震安全，本橋在縱橋向建議在塔梁交接處布置4個阻尼器。

4.2 橫橋向

前期分析表明過渡墩是本橋橫向抗震的薄弱環節。由于過渡墩處支座布置在橫橋向上不對稱，框架墩的3個立柱受力不完全相同，因此本文對這3個截面均予以分析，計算結果見表4—5及圖7。

由表4—5可知，在初步設計的支座布置下，在過渡墩處設置單側和雙側阻尼器對各構件幾乎沒有減震效果。結合表1可知，不論是否設置阻尼器，過渡墩3個立柱都將進入“可修復損傷”狀態。若將過渡墩支座布置由DX+SX改為SX+SX，并布置雙側阻尼器后，過渡墩彎矩和剪力響應會大幅下降。相比無阻尼器時，S1～S3截面的彎矩減震率分別為34.8%、37.8%和36.5%。結合表1可知，此時過渡墩將保持“無損傷”狀態。值得一提的是，過渡墩約束方式的改變對索塔地震響應幾乎沒有影響。

由圖7可知，在初步設計的支座布置下，不論是否設置阻尼器，過渡墩單向支座的剪力都大大超出其抗剪能力(見表1)，且阻尼器幾乎不起作用，其原因在于阻尼器發揮功效有賴于其沖程速度(見公式(1))。由于單向支座的存在，主梁在過渡墩處的橫向運動受到限制，其相對于墩的速度很小，因此阻尼器無從發揮作用。索塔處的支座剪力同樣超出其抗剪能力，即使改變過渡墩支座布置后，也沒有明顯改善。由于索塔處設置了橫向抗風支座，可有效地分擔球鋼支座的橫向剪力，限于篇幅，本文不作重點介紹。過渡墩的抗震性能得到大幅改善，但其支座變形達69.1 mm，超過了表1中50 mm的變形能力。為此，后文對阻尼器性能參數進行了優化分析，以控制過渡墩支座的橫向變形。

表4 3種方案地震彎矩對比

表5 3種方案地震剪力對比

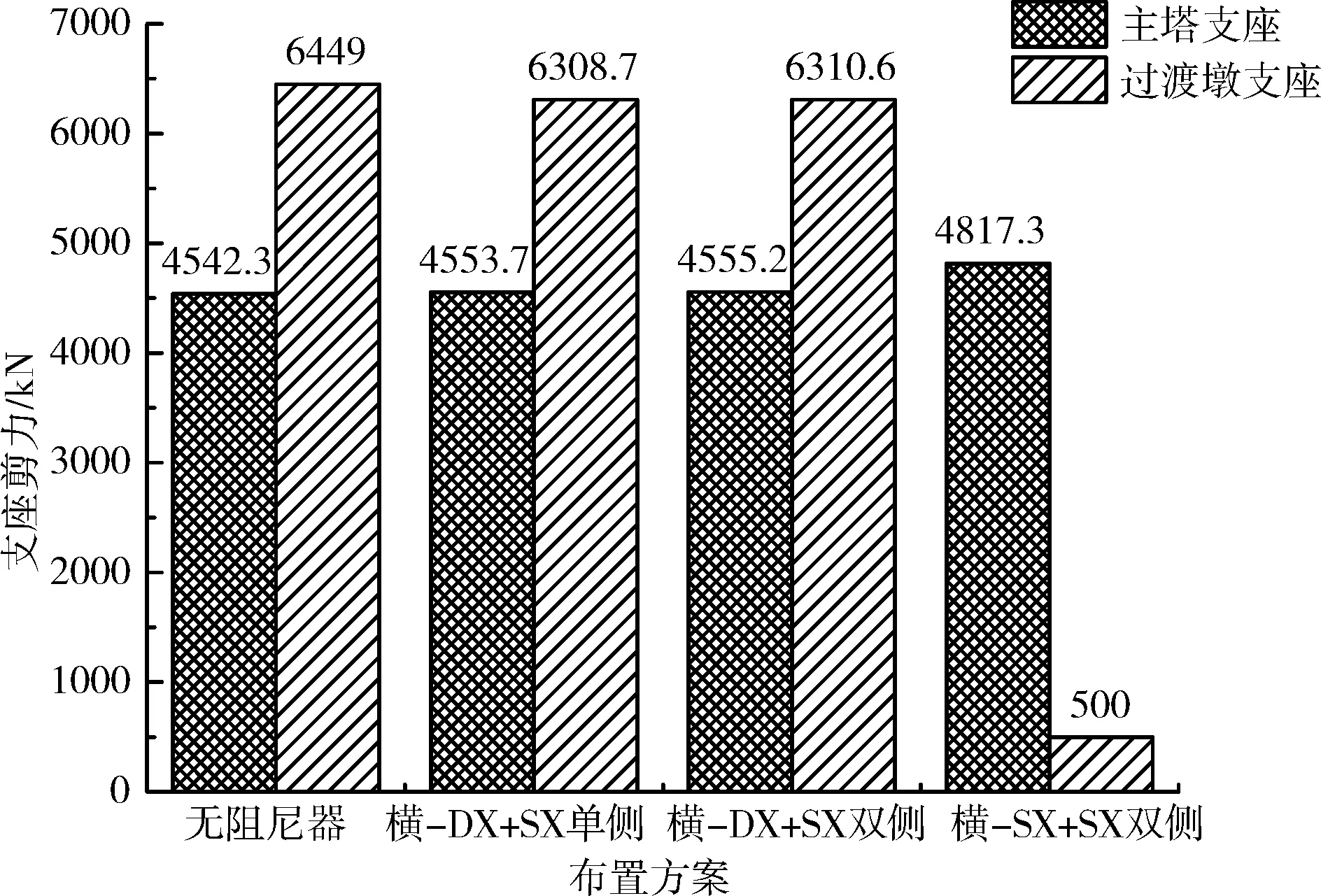
注：由于改變了支座布置，“橫-SX+SX雙側”中過渡墩處已無單向支座，因此其支座剪力為摩擦力。

圖7 3種方案支座剪力對比

5 阻尼器參數優化分析

由公式(1)可知，粘滯阻尼器耗能能力與性能參數C和ξ密切相關。為此，本文針對4.2節中的“橫-SX+SX雙側”工況開展阻尼器參數優化分析，以討論阻尼器性能參數對橋梁減震率的影響，同時確定保證橋梁抗震安全的合理參數，為工程設計提供依據。為了降低計算量，采用逐一優化方式來選擇參數，首先保持C=3 000 kN/(m/s)ξ不變，分別令ξ=0.1，0.2，0.3，……，0.9，由此確定最優ξ值；然后保持ξ值不變，令C=1 000、2 000、3 000、4 000、5 000 kN/(m/s)ξ，由此確定最優C值。由表4—5可知，過渡墩上阻尼器布置方式對主塔幾乎沒有影響，因此本節重點分析過渡墩及支座的地震響應。

如圖8所示，隨著阻尼指數ξ的增大，過渡墩3個立柱的彎矩和剪力響應都經歷了先減后增的過程。當ξ=0.7時，過渡墩內力最小。如圖9所示，過渡墩支座的橫向變形隨阻尼指數ξ的增大而增大，滿足支座容許變形時，ξ取值不能超過0.3。結合表1可知，當ξ=0.3時，過渡墩仍處于“無損傷”狀態，因此阻尼指數的最優值取ξ=0.3。

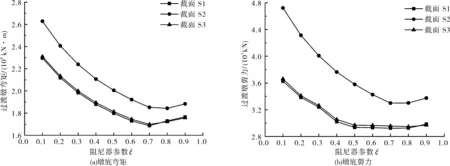
圖8 ξ對過渡墩地震內力的影響

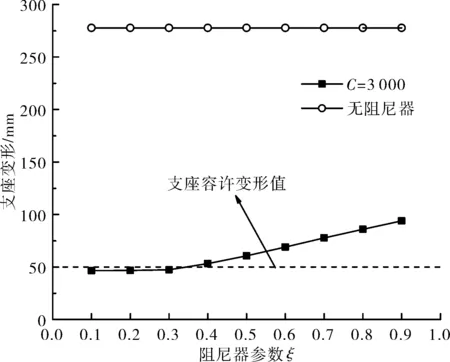
圖9 ξ對過渡墩支座橫向變形的影響

由圖10—11可知，隨著阻尼系數C的增大，過渡墩內力單調增大，支座變形則單調下降。根據表1，若要保持過渡墩處于“無損傷”狀態，且支座變形低于其容許值，那么阻尼器的優化參數應取ξ=0.3、C=3 000 kN/(m/s)ξ。在此參數下，過渡墩3個立柱的墩底彎矩分別為19 841.44、22 391.15、19 995.722 kN·m，均低于“無損傷”狀態的彎矩；支座橫向變形為47.4 mm，也低于50 mm的容許變形。

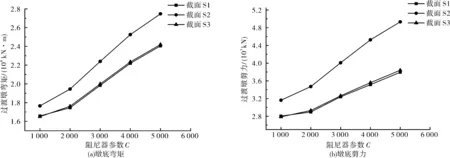
圖10 C對過渡墩地震內力的影響

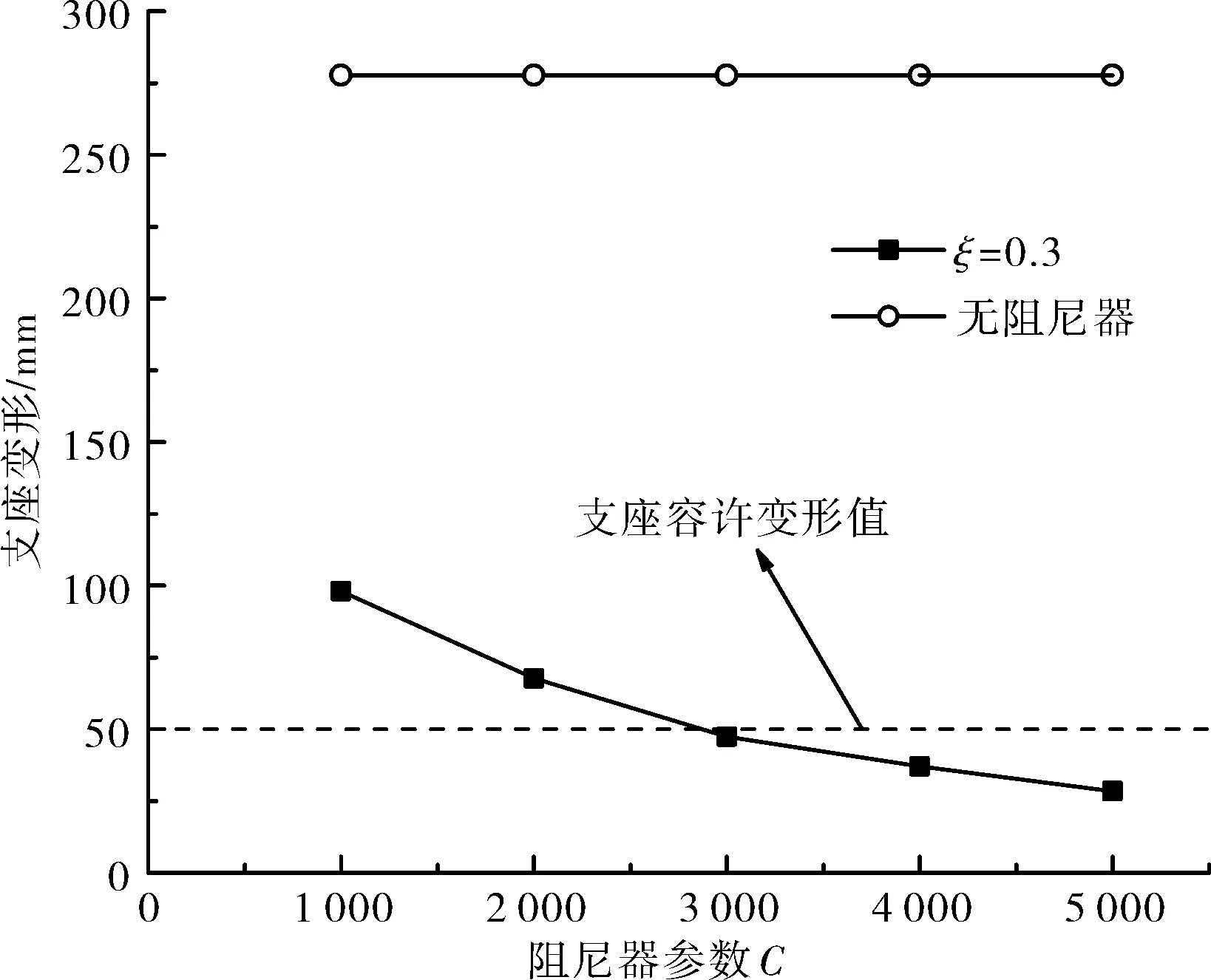
圖11 C對過渡墩支座橫向變形的影響

6 結論

本文針對某新建半漂浮體系斜拉橋，通過縱、橫橋向阻尼器布置及其性能參數的優化分析，得到如下結論。

1)在初步設計的支座布置下，主梁在縱橋向為半漂浮體系，其地震慣性力主要通過拉索傳遞至索塔，輔助墩和過渡墩分擔很小；而在橫橋向，主梁地震慣性力主要由索塔和過渡墩承擔，輔助墩由于布置雙向支座，參與程度很低。

2)在縱橋向，如果不設置阻尼器，索塔將進入“局部破壞”狀態，過渡墩支座的縱向變形超限。當在塔梁交接處布置4個阻尼器時，索塔可保持“無損傷”狀態，支座變形也低于容許值。

3)在橫橋向，若保持初步設計的支座布置，那么不論是否設置阻尼器，過渡墩都將進入“可修復損傷”狀態，且阻尼器作用很小。將過渡墩支座布置由DX+SX改為SX+SX，并布置雙側阻尼器后，過渡墩地震內力會大幅下降。

4)在橫橋向，過渡墩上支座和阻尼器的布置方式對索塔地震響應幾乎沒有影響。隨著阻尼指數ξ的增大，過渡墩地震內力先減后增，而支座變形則單調遞增；隨著阻尼系數C的增大，過渡墩地震內力單調遞增，而支座變形則單調下降。為了保持過渡墩處于“無損傷”狀態，且支座變形低于容許值，那么阻尼器的最優參數分別為ξ=0.3、C=3 000 kN/(m/s)ξ。