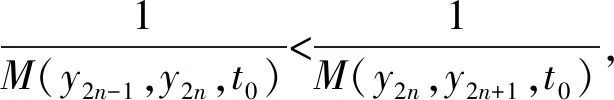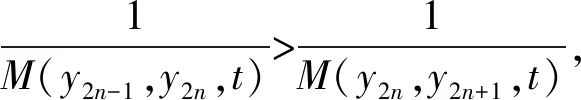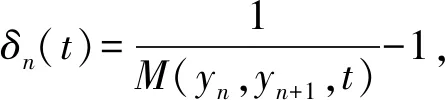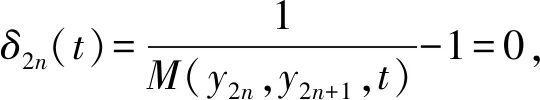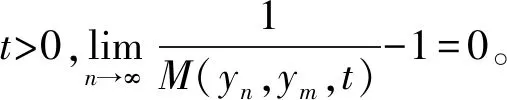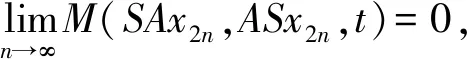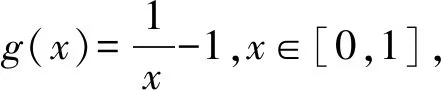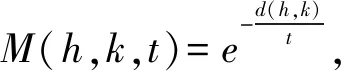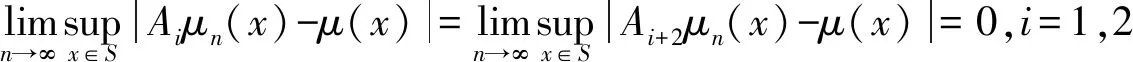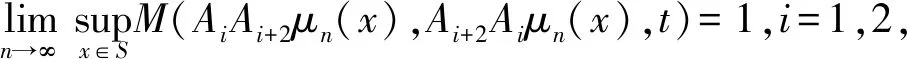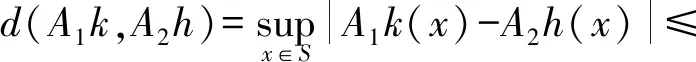模糊度量空間中公共不動(dòng)點(diǎn)定理及其在動(dòng)態(tài)規(guī)劃中的應(yīng)用
張樹(shù)義,張芯語(yǔ), 聶 輝
(渤海大學(xué)數(shù)理學(xué)院, 遼寧 錦州 121013)
1 引言與預(yù)備知識(shí)
關(guān)于模糊度量空間概念以及在此空間中建立的不動(dòng)點(diǎn)定理,文獻(xiàn)[1-15]做過(guò)廣泛研究,這其中文獻(xiàn)[14]引入模糊度量M滿足三角不等式的概念,并在模糊度量空間中得到一些不動(dòng)點(diǎn)定理。 文獻(xiàn)[16]推廣了上述相關(guān)結(jié)果,在模糊度量空間中研究了兩類(lèi)Φ-壓縮映象的一些不動(dòng)點(diǎn)定理,并討論了一類(lèi)泛函方程解的存在性。文獻(xiàn)[17]在概率度量空間中研究了拓?fù)浣Y(jié)構(gòu)和度量化問(wèn)題。近些年來(lái),文獻(xiàn)[18-26]研究了若干類(lèi)非線性映象不動(dòng)點(diǎn)的存在性。受上述工作啟發(fā),本文將文獻(xiàn)[16]的結(jié)果推廣到更一般的情形,在模糊度量空間建立了涉及4個(gè)映象的更廣泛的Altman型映象的公共不動(dòng)點(diǎn)存在性定理,從而改進(jìn)和推廣了文獻(xiàn)[6-26]中的相應(yīng)結(jié)果。作為應(yīng)用,我們?cè)谀:攘靠臻g中還討論了起源于動(dòng)態(tài)規(guī)劃的一類(lèi)泛函方程組解的存在與唯一性。
定義1 映象*:[0,1]×[0,1]→[0,1]稱(chēng)為連續(xù)t-范數(shù),如果滿足以下條件:
(ⅰ) *是可結(jié)合和可交換的;
(ⅱ) *是連續(xù)的;
(ⅲ) ?a∈[0,1],a*1=a;
(ⅳ) ?a,b,c,d∈[0,1],若a 定義2 稱(chēng)三元組(X,M,*)是一模糊度量空間,若X是一任意非空集合,*是一連續(xù)t-范數(shù),M是X×X×(0,+∞)上的模糊集,對(duì)?x,y,z∈X和t,s>0,滿足以下條件: (Ⅰ)M(x,y,t)>0; (Ⅱ)M(x,y,t)=1 當(dāng)且僅當(dāng)x=y; (Ⅲ)M(x,y,t)=M(y,x,t); (Ⅳ)M(x,y,t)*M(y,z,s)≤M(x,z,t+s); (Ⅴ)M(x,y,·)∶(0,+∞)→[0,1]是連續(xù)的。 如果(X,M,*)是一模糊度量空間,稱(chēng)(M,*)是X上模糊度量。 注1 設(shè)(X,Md,·)如例1所述是一標(biāo)準(zhǔn)模糊度量空間,則(X,Md,·)是完備的當(dāng)且僅當(dāng)度量空間(X,d)是完備的。 定義3 三元組(X,M,*)稱(chēng)為非阿基米德模糊度量空間,若(X,M,*)是一模糊度量空間,*是滿足下列條件的*-范數(shù)。 (Ⅵ)M(x,z,max{t1,t2})≥M(x,y,t1)*M(y,z,t2),?t1,t2∈[0,∞),?x,y,z∈X。 George 和Veeramani[4]給出了如下結(jié)論 (ⅰ) 設(shè)(X,M,*)是一模糊度量空間,稱(chēng)B(x,r,t)={y∈X:M(x,y,t)>1-r},?r∈(0,1),t>0為具有中心x∈X,半徑r的開(kāi)球。一族集{B(x,r,t):x∈X,0 (ⅱ) 模糊度量空間(X,M,*)中序列{xn}收斂于x當(dāng)且僅當(dāng)M(xn,x,t)→1(n→∞)。 (ⅲ) 模糊度量空間(X,M,*)中序列{xn}稱(chēng)為Cauchy序列,如果對(duì)?r∈(0,1)和t>0,存在n0∈N(正整數(shù)集),使得n,m≥n0,M(xn,xm,t)>1-r。 模糊度量空間(X,M,*)稱(chēng)為完備的,如果每一Cauchy 序列{xn}在X中收斂。 定義4[8]設(shè)(X,M,*)是模糊度量空間,模糊度量M稱(chēng)為三角的,如果?x,y,z∈X,?t>0,有 注意到每個(gè)標(biāo)準(zhǔn)模糊度量(Md,·)是三角的。 設(shè)Ω={g|g:[0,1]→[0,∞) 連續(xù),嚴(yán)格遞減,g(1)=0}。 定義5 非阿基米德模糊度量空間(X,M,*)稱(chēng)為(C)g型的。如果存在g∈Ω,使得?x,y,z∈X,?t≥0,有g(shù)M(x,y,t)≤gM(x,z,t)+gM(z,y,t)。 定義6 非阿基米德模糊度量空間(X,M,*)稱(chēng)為(D)g型的,如果存在g∈Ω,使得?s,t∈[0,1],有g(shù)(s*t)≤g(s)+g(t)。 定義7 設(shè)模糊度量空間(X,M,*),映象S,A:X→X稱(chēng)為相容映象,如果對(duì){xn}?X,當(dāng) 下列引理在后面將被用到 引理1 設(shè)(X,M,*)是模糊度量空間,S,A:X→X是相容映象,如果Az=Sz,z∈X,則ASz=SAz。 引理2 (ⅰ) 如果非阿基米德模糊度量空間(X,M,*)是(D)g型的,則(X,M,*)是(C)g型的。 這表明(X,M,*)是(D)g型的。證畢。 定義Φ1={φ:φ:[0,∞)→[0,∞) 是單調(diào)遞增滿足(c1),(c2)和(c3)},其中條件(c1),(c2)和(c3)如下: (c1) 0<φ(u) 注3 如果φ∈Φ1,則φ(0)=0且φ(u)=u?u=0。 定理1 設(shè)(X,M,*)是具有M三角的完備模糊度量空間,設(shè)(S,A),(T,B)是X→X的相容映象,AX?TX,BX?SX,使得?x,y∈X,?t>0,有 (1) 其中?x,y∈X,t>0,Φ∈Φ1。如果S,T,A,B連續(xù),則S,T,A,B在X上有唯一公共不動(dòng)點(diǎn)。 證明任取x0∈X作序列 y2n=Ax2n=Tx2n+1,y2n+1=Bx2n+1=Sx2n+2(n=0,1,2,…),由(1) 對(duì)?t>0,有 同理對(duì)?t>0,有 于是對(duì)n=0,1,2,…,?t>0,有 所以Bv=Au,于是Su=Au=Bv=Tv=c,進(jìn)而由引理1有Sc=Ac,Bc=Tc。 于是對(duì)?t>0,由(1)和(c1)有 所以Sc=Tc=Bc=Ac。下證c是S,T,A,B在X上公共不動(dòng)點(diǎn)。由(1)和(c1)對(duì)?t>0,有 所以Sz=Tz=Bz=Az=w。下證w是S,T,A,B在X上公共不動(dòng)點(diǎn)。由于(S,A)是相容映象,故由引理1有Sw=ASz=SAz=Aw。 又因?yàn)?T,B)是相容映象,所以Tw=TBz=BTz=Bw。 由(1) 對(duì)?t>0,有 于是w=Bw,故w是S,T,A,B在X上公共不動(dòng)點(diǎn)。唯一性顯然。證畢。 設(shè)(X,Md,*)是由X上度量d誘導(dǎo)的完備標(biāo)準(zhǔn)模糊度量,則Md是三角的,于是由定理1,我們有下列推論。 推論1 設(shè)(X,d) 是完備度量空間,(S,A),(T,B)是X→X的相容映象對(duì),AX?TX,BX?SX,?x,y∈X,滿足如下不等式 如果S,T,A,B連續(xù),則S,T,A,B在X上有唯一公共不動(dòng)點(diǎn)。 定理2 設(shè)(X,M,*)是完備非阿基米德模糊度量空間,其中連續(xù)t-范數(shù)為a*b=min{a,b},a,b∈[0,1],再設(shè)(S,A),(T,B)是X→X的相容映象,AX?TX,BX?SX。使得?x,y∈X,?t>0,有 其中Φ∈Φ1。如果S,T,A,B連續(xù),則S,T,A,B在X上有唯一公共不動(dòng)點(diǎn)。 設(shè)R=(-∞,+∞),X和Y是實(shí)Banach空間,S?X為狀態(tài)空間,D?Y為決策空間,B(S)是S上有界實(shí)函數(shù)全體,x和y分別為狀態(tài)向量和決策向量,T為過(guò)程變換,f(x)為具有初始狀態(tài)x的最優(yōu)返回。下面我們利用在模糊度量空間中建立的涉及4個(gè)映象的Altman型映象的公共不動(dòng)點(diǎn)定理,討論下列起源于動(dòng)態(tài)規(guī)劃的泛函方程組解的存在與唯一性: (2) 其中i=1,2,3,4,x∈S,opt=sup或opt=inf,u:S×D→R,T:S×D→S,H:S×D×R→R。 定理3 假設(shè)下列條件成立: (a1)u,Hi(i=1,2,3,4)有界; (a2)對(duì)任意(x,ξ,y)∈S×S×D,k,h∈B(S)和t>0,有 對(duì)x∈S,y∈D,k,h∈B(S),t∈S,其中Φ∈Φ1, (a3)A1(B(S))?A4(B(S)),A2(B(S))?A3(B(S)); (a4)對(duì)Ai(i=1,2,3,4),滿足任意的{γn}n≥1?B(S),γ∈B(S),有 (a5)對(duì)任意的{μn}n≥1?B(S),如果存在μ∈B(S),當(dāng) 證明任意的h,k∈B(S),定義d(h,k)=sup{|h(x)-k(x)|,x∈S},由(a1)可知, Ai:B(S)→B(S),i=1,2,3,4。 由(a4)和(a5),A1,A2,A3,A4是連續(xù)的,并且A1與A3,A2與A4是相容的。 若opt=sup,則由(a2)中Aiqi(x)的定義,對(duì)任意的k,h∈B(S),x∈S,對(duì)任意的ε>0,存在y,z∈D,有下列不等式成立: A1k(x) A1k(x)≥u(x,z)+H1(x,z,k(T(x,z))),A2h(x)≥u(x,y)+H2(x,y,h(T(x,y)))。 由上面不等式容易得到 A1k(x)-A2h(x) 和 A1k(x)-A2h(x)>H1(x,z,k(T(x,z)))-H2(x,z,h(T(x,z)))-ε≥ 令ε→0,得 進(jìn)而由條件(ⅱ)有 因此 (3) 如果opt=inf,類(lèi)似的,(3)也成立。由定理2我們立刻獲得A1,A2,A3,A4有唯一不動(dòng)點(diǎn)w∈B(S),即w是泛函方程(2)在B(S)上的唯一解。證畢。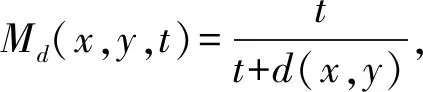
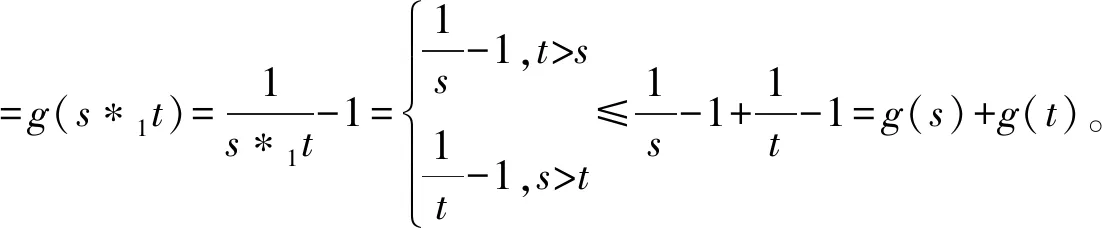
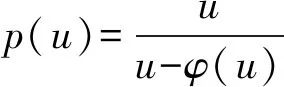
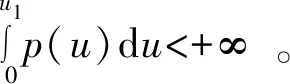
2 主要結(jié)果