第二代完整穩性衡準研究最新進展

王志榮， 周耀華， 戶艷宏

(1.中國船級社， 北京 100007； 2.中國船級社 上海規范研究所， 上海 200135)

0 引 言

船舶穩性作為事關人命安全的重要性能指標，一直以來受到國際海事組織(IMO)的高度關注。在大量的事故統計資料和研究成果基礎上，IMO制定了強制性的完整穩性和破損穩性法定要求[1-2]，但其中的完整穩性規則主要側重于癱船模式，并不涉及諸如參數橫搖、純穩性喪失、騎浪和過度加速度等波浪中的動穩性失效模式。隨著包括集裝箱船“APL CHINA”(C11)在內的若干實船事故的發生[3]，IMO有針對性地開展了第二代完整穩性衡準的制定工作。衡準包含參數橫搖、純穩性喪失、騎浪/橫甩、癱船穩性和過度加速度等5種穩性失效模式。目前，IMO基本完成了薄弱性衡準(第一層薄弱性衡準和第二層薄弱性衡準)的制定工作，并起草了穩性直接評估流程指南等衡準草案文本，相關技術文件形成了由5種失效模塊、3層評估方法以及航行作業指南構成的第二代完整穩性衡準構架體系。

雖然第二代完整穩性衡準的制定工作已經取得了巨大進展，但尚存幾方面的問題有待解決，包括參數橫搖薄弱性衡準第二層運動預報方法的選取、薄弱性衡準的一致性驗證、純穩性衡準的一致性改進、用于穩性直接評估計算方法的精度驗證指標研究等。對此，根據工信部批準的“第二代完整穩性衡準的應對和純穩性喪失直接評估技術研究”項目，國內相關的設計和研究單位相繼開展了船舶完整穩性5種失效模式的大量研究，包括大規模實船驗證計算，研發具有獨立知識產權的第二代完整穩性衡準評估軟件，積極參與IMO第二代完整穩性衡準的制定等。相關成果以提案形式代表中國向IMO提交，其中SDC 4會議(2017)和SDC 5會議(2018)總計提交13份提案，極大地促進了新衡準的制定和完善工作，提高了中國在規則制定方面的發言權。

1 參數橫搖Level2衡準運動預報方法選型

學術界及各國政府針對參數橫搖Level 2衡準的運動預報方法以及實船敏感性預報開展了大量卓有成效的研究。截至2015年，IMO相關研究均基于采用平均法(Averaging Method, AVM)[4]開展，該方法通過求解單自由度非線性橫搖方程獲得參數橫搖的穩態解。在2016年召開的IMO船舶設計建造分委會第三次會議(SDC 3)上，對于參數橫搖Level 2衡準新增加了同樣基于非線性力學方法的時域法(Time Domain Method, TDM)[5]作為備選方案。IMO希望通過發起新一輪衡準運動預報方法的選型研究，確保最終方案對于不同類型的實船均具有較好的工程適用性和預報精度。

1.1 基于求解穩態解的平均方法

該方法采用簡化的橫搖單自由度(1 Degree of Freedom, 1 DOF)方程開展參數橫搖幅值的預報和敏感性分析。這種方法的主要思路是通過對不同船波相對位置下的波浪中初穩心高(TDM-GM， 量符號是hGM)和靜水回復力臂(TDM-GZ， 量符號是LGZ)曲線進行擬合，模擬波浪中GZ曲線的周期性變化。其運動方程[2]為

(1)

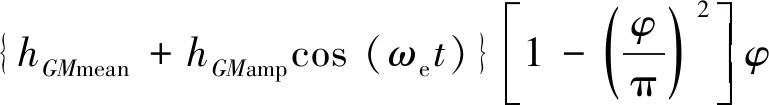
(2)

式中：φ為橫搖角；hGMmean為波浪中穩心高變化量的平均值；hGMamp為波浪中穩心高變化量的幅值；ωφ為橫搖固有圓頻率；ωe為遭遇頻率；l2k+1為采用最小二乘法擬合靜水中的GZ曲線得到的擬合系數，k為擬合階數；α、γ分別為線性和三次橫搖阻尼系數；t為時間。

1.2 求時域解的時域方法

該方法的主要思路是通過對不同船波相對位置下的波浪中初穩心高和波浪中靜水回復力臂GZ曲線進行制表插值的方法，模擬波浪中GZ曲線/GM值的周期性變化。其運動方程為

sign(φ)ρgLGZ(t,|φ|)=0

(3)

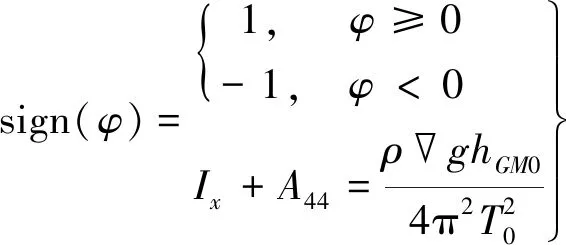
(4)

式中：Ix+A44為橫搖慣性矩和附加慣性矩；為排水體積；ρ為海水密度；g為重力加速度；hGM0為靜水中初穩心高；T0為橫搖固有周期；δ1=2α，δ3=γ為阻尼因數，可采用簡化Ikeda方法計算；LGZ(t,|φ|)為波浪中LGZ值，即船與入射波處于時刻t的相對位置，波浪中對應橫搖角φ的GZ曲線取值。

1.3 研究進展

由于備選的時域方法的若干重要計算參數的設置尚未確定，有必要通過驗證獲得適當的取值，確保計算結果的穩定性。采用兩艘集裝箱船(S25、C11)和一艘車輛滾裝船(S10)的模型試驗數據，驗證、對比兩種備選方法的預報精度，分析各方法精度差異的原因，最后針對中國不同類型的大量實船裝載工況及事故船進行敏感性水平預報，通過對比分析平均法和時域法的敏感性計算結果，為Level 2衡準參數橫搖運動預報方法的選型給出若干建議。

表1和圖1為樣船主尺度和試驗船模照片。圖2和圖3為部分精度驗證結果[6]。基于模型試驗的精度驗證，進一步開展兩種數值模擬方法的實船敏感性預報結果對比。圖4為基于38艘各類型實船的衡準敏感性校核計算結果對比。通過以上研究，驗證AVM和TDM的計算精度及其對實船敏感性預報的影響。對于IMO參數橫搖Level 2衡準，建議選取AVM和TDM作為運動預報方法。試驗對比驗證和實船敏感性計算表明兩者均能給出趨勢相似、偏于保守的預報結果，且敏感性預報結果差異較小。當采用AVM和TDM時，標準值可維持現有值不變。相關研究成果已作為技術提案提交IMO討論[7]。

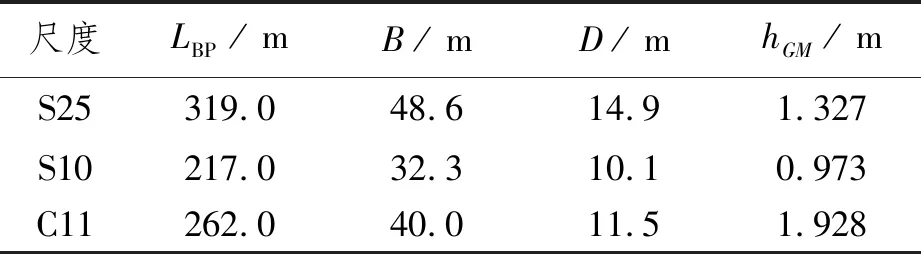
表1 船舶主尺度(實船尺度)

圖1 S25船模示例

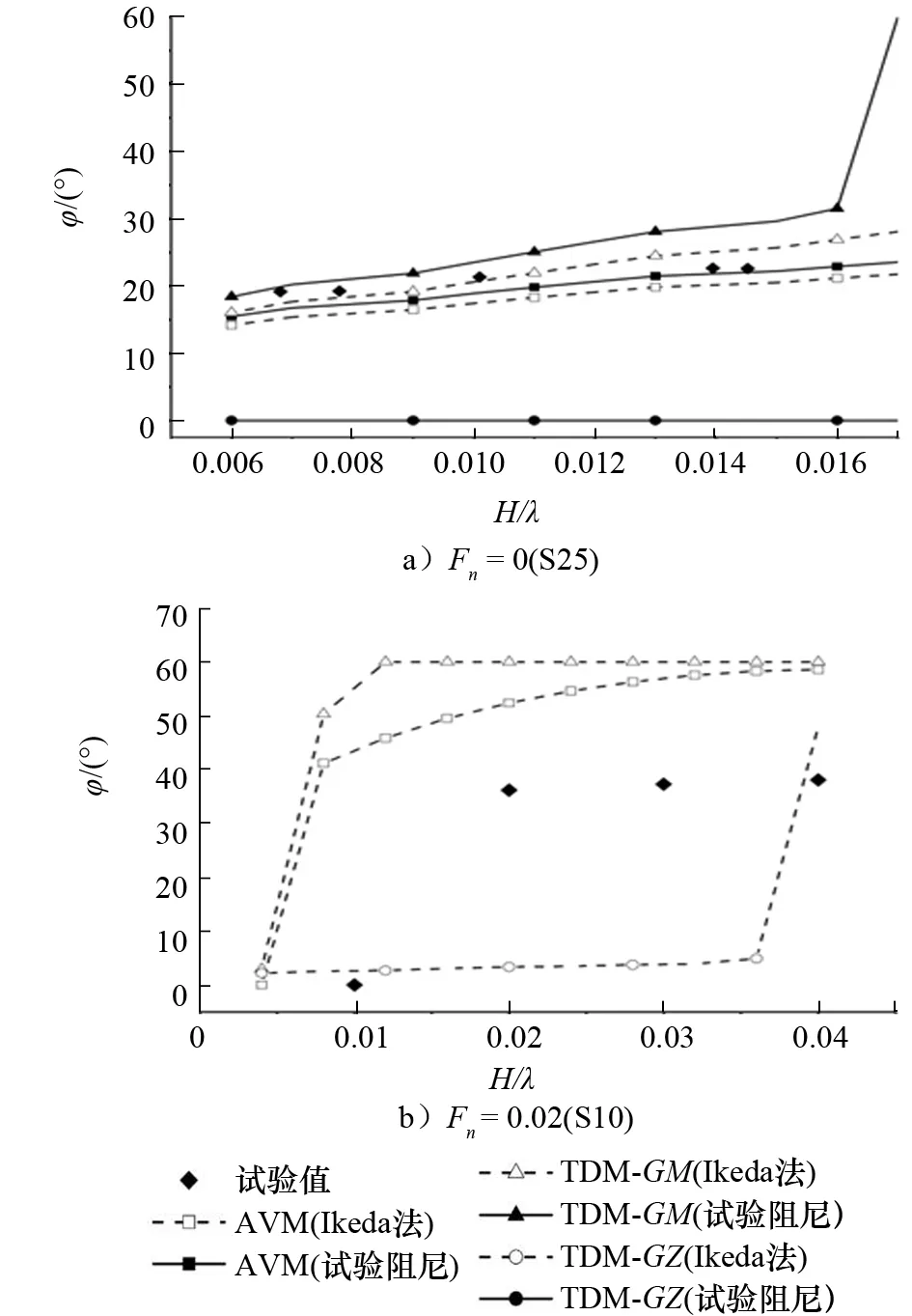
圖2 S25船和S10船迎浪參數橫搖幅值[6]

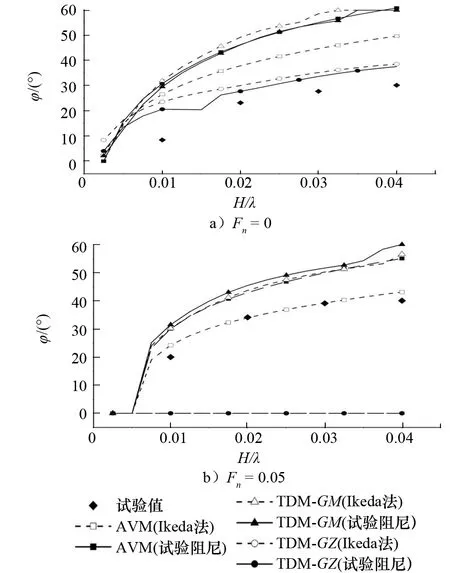
圖3 C11船迎浪參數橫搖幅值

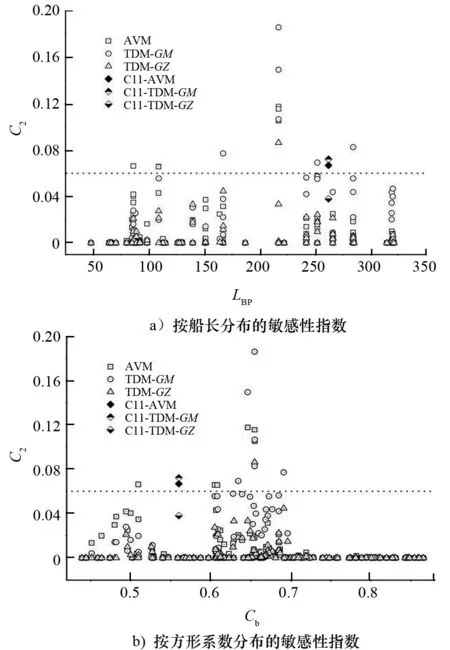
圖4 38艘各類型實船衡準敏感性指數C2

2 參數橫搖和純穩性喪失薄弱性衡準一致性檢驗

根據IMO對第二代完整穩性衡準的基本構架體系，3層評估方法的計算復雜性依次遞增，評估準確性也依次提高。只有在第一層薄弱性衡準沒有通過的情況下，才進行第二層薄弱性衡準的評估；在無法通過第二層薄弱性衡準時，進行第三層評估——穩性直接評估；在3層衡準評估都無法通過時，必須對船型進行重新設計或制定航行操作指南，以避免穩性失效的發生。對于薄弱性衡準而言，早期研究階段曾出現過滿足第一層衡準的要求卻無法滿足第二層衡準要求的情況，即產生了所謂的一致性問題。IMO于SDC 3會議上決定在2016年度開展衡準樣船計算，進一步檢驗衡準樣船結果的一致性。國內根據IMO的工作計劃，針對中國大量實船開展了校核計算，結合中國普通商業運營船舶對5種失效模式的敏感性，著重針對中國船舶開展參數橫搖、純穩性喪失和過度加速度薄弱性衡準的一致性檢驗。

2.1 參數橫搖衡準

參數橫搖是在縱向大幅波浪(迎浪或隨浪)中，由復原力臂曲線周期性變化導致的一種參數激勵共振現象。

第一層薄弱性衡準是通過經驗公式判斷船舶在等效規則波中初穩心高的變化幅度來確定敏感性，經驗公式為

(5)

第二層薄弱性衡準是基于概率方法，對航行在北大西洋海域的船舶，計算其發生參數橫搖的概率，分第一次校核和第二次校核兩部分。第一次校核是對第一層薄弱性衡準的擴展，第二次校核是采用單自由度非線性橫搖運動方程計算等效規則波下的參數橫搖幅值，并進行不規則波中的敏感性指數加權計算，得到最終的敏感性指數C2。第二次校核包括AVM和(TDM-GM、TDM-GZ)兩種，參見第1.1節和第1.2節。

2.2 純穩性喪失

純穩性喪失是由隨浪航行時船舶復原力臂減小而導致的穩性失效模式。此衡準的核心是判斷波浪中船舶GZ曲線的穩性特征，計算入射波條件規定的等效入射波與船舶處于規定的若干位置時的GZ曲線，通過判斷GZ曲線的若干特征計算敏感性指數，并依據海況發生概率進行加權計算，得到最終的敏感性指數[8]。

入射波直接采用國際船級社協會推薦的不規則波散布圖[9]中的272個海況，換算為波長與船長比為1.0的等效規則波，對每個海況進行敏感性指數加權計算，由波浪中穩性特征判斷[10]。

(6)

式中：φv為穩性消失角與進水角的較小值，取入射波與船舶11個相對位置對應的波浪中GZ曲線中該角度最小值；RPL1=30°為標準值。

(7)

式中：φs為等效波中10個位置對應GZ曲線與力臂值RPL3平衡角度的最大值；RPL2對客船為15°，對其他船舶為25°。

最終，衡準校核加權得到敏感性指數最大值max(CR1,CR2)。

2.3 過度加速度

過度加速度是船舶橫搖等運動導致橫向加速度過大的現象，主要對貨物造成損壞，嚴重時造成人員傷害。

第一層薄弱性衡準是采用簡單的經驗公式，以固有周期的共振橫搖估算最大加速度值。

第二層薄弱性衡準是通過頻域求解單自由度線性橫搖運動方程[11]，根據計算出的橫搖響應算子計算不規則波中的加速度響應，再進行敏感性指數加權計算，得到敏感性指數C。

(8)

θ=θaei ωet

(9)

MFK=(a+bi)·ei ωet

(10)

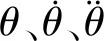
2.4 國內研究進展

在工信部二代穩性項目實施中，采用了兩種方式開展一致性檢驗，包括假定裝載工況的矩陣計算和經批準的實際裝載工況校核計算。假定裝載工況矩陣是根據批準的實際裝載工況吃水和hGM范圍組合假定而成的，矩陣中常有不同數量的工況在實際運營中不會出現。因此，該矩陣計算僅具備一定的參考意義，更適合于開展許用GM曲線的計算。經批準的實際裝載工況是指滿足目前生效的2008國際完整穩性規則的要求，經主管機關批準可用于安全運營的實際工況。矩陣計算樣船采用4艘集裝箱船、1艘滾裝船、2艘LNG船、2艘海洋供應船(Offshore Support Vessels, OSV)、2艘救助船和3艘客船，總計14艘樣船。經批準的實際裝載工況校核計算采用11艘實船，包括1艘集裝箱船、1艘LPG船、1艘打撈起重船、1艘瀝青運輸船、1艘滾裝船、3艘OSV和3艘海洋調查船。樣船和實船主尺度如表2所示。圖5給出了部分樣船矩陣計算結果,橫坐標為不同計算工況的吃水和hGM值，縱坐標為根據不同衡準方法計算得到的敏感性結果與標準值的差值。通過以上研究得到了這3種失效模式的一致性檢驗結果。研究表明對于中國樣船而言，一致性問題主要集中于純穩性喪失衡準。據此，確立了中國對于一致性問題的基本立場[12-13]，為后續開展薄弱性衡準改進研究確立了研究方向。

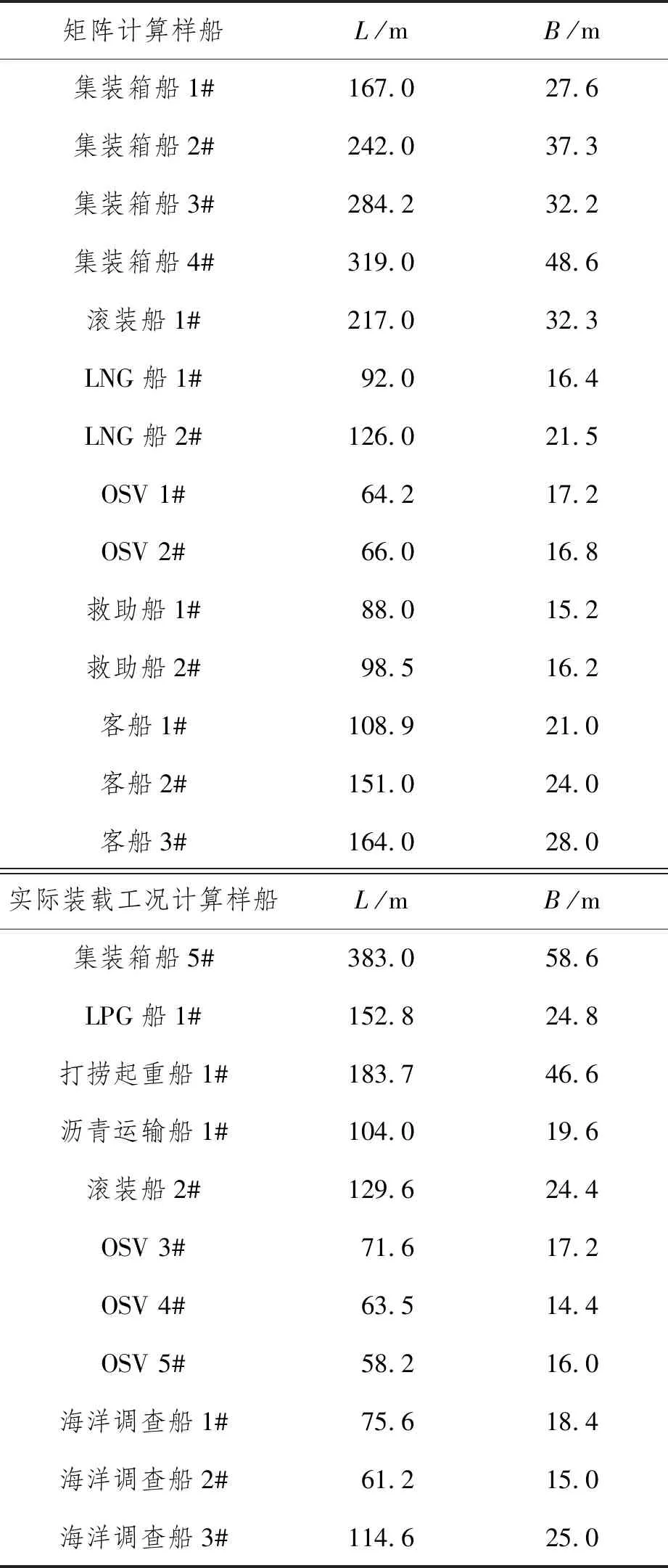
表2 矩陣計算樣船與實際裝載工況計算樣船尺度

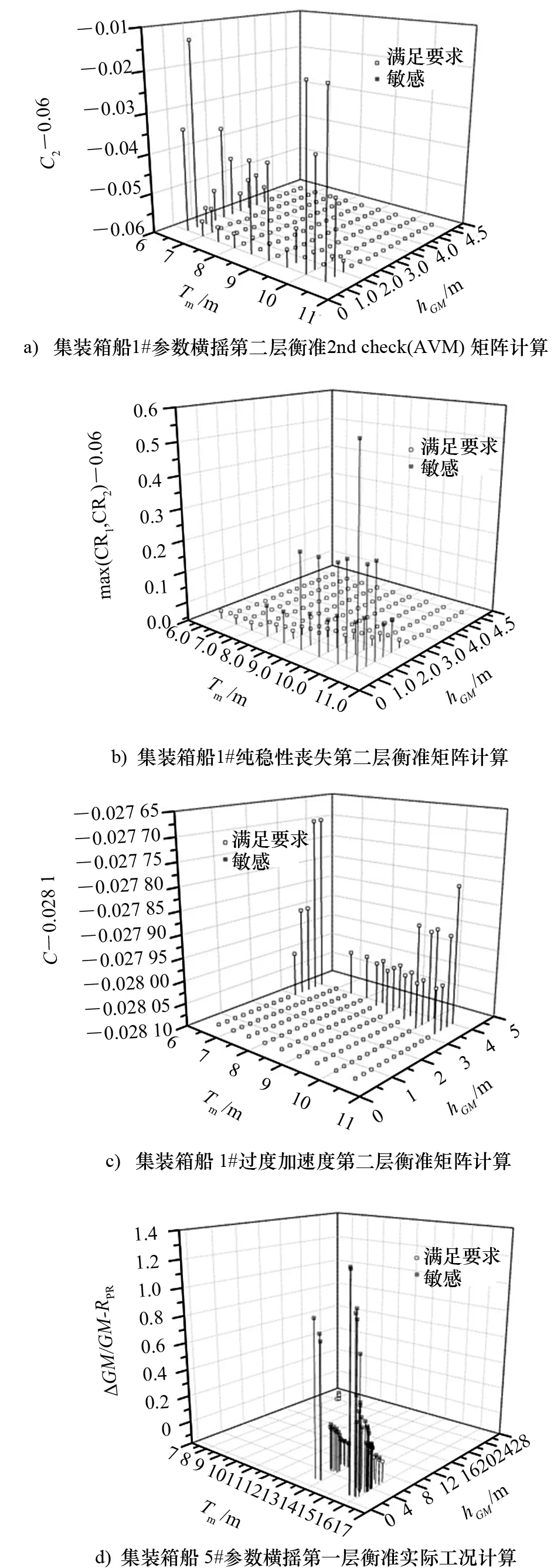
圖5 部分矩陣和實際工況計算結果

3 純穩性薄弱性衡準的一致性改進

3.1 SDC4會議改進建議

針對純穩性喪失衡準通過樣船計算結果表現出來的一致性問題，IMO在SDC 4會議上對解決方案進行了討論。提高第一層衡準的入射波條件，將入射波陡由現有的0.03提高至0.05。通過提高第一層衡準保守程度的方式改善一致性。根據這一提議，開展了11艘典型實船的對比計算，如表3所示。由對比計算結果可見，3艘OSV和2艘海洋調查船仍然存在一致性問題，這表明SDC 4會議考慮的改進措施實質上對于OSV和海洋調查船型改善效果不明顯。

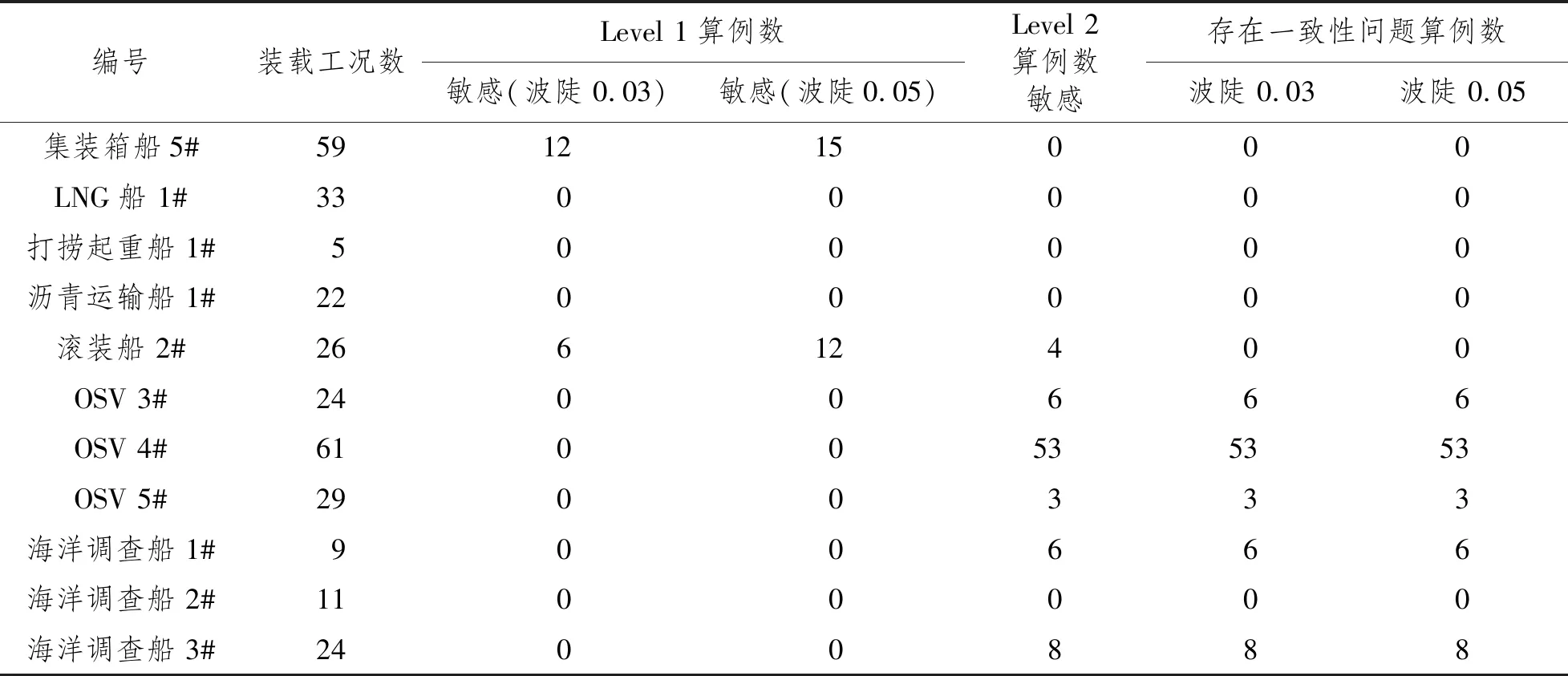
表3 算例數對比結果統計

3.2 國內針對一致性改進的方案

由于驗證表明SDC 4會議的改進建議均未能有效地改善一致性，因此有必要進一步研究全新的改進措施。分析既往純穩性喪失樣船計算結果發現，一致性問題可能由兩個方面的原因所導致：(1)由于現有第一層衡準的等效波陡取為固定值，對于中小尺度船舶，等效入射波所表征的海況將會降低；(2)第二層衡準中增加了校核船舶抵御橫傾力矩RPL3能力的要求(即對GZ曲線的特征隱含了要求)，而第一層衡準僅校核波浪中最小初穩心高，后者無法完全反應船舶波浪中GZ曲線的特征。據此，提出針對薄弱性衡準的改進建議：首先，改進入射波陡假定的合理性，對于第一層衡準的入射波陡系數Sw，可改為采用有義波高Hs=7.5 m、平均跨零周期Tz=6.5～18.5 s計算得到的等效波陡中的最大值；其次由于現有的最小hGM值衡準實際無法完全反映波浪中GZ曲線特性，因此無法完全反映船舶抵御橫傾力矩RPL3的能力。有鑒于此，提議對于第一層衡準，新增對于RPL2對應波浪中LGZ值的判斷。

采用修改方案后，不同尺度船舶的校核海況得到了統一。針對所提出的純穩性喪失第一層衡準的改進建議，開展樣船對比計算驗證其有效性。計算樣船包括11艘實船。圖6給出了第一層判定敏感的裝載工況比例，以及存在一致性問題的裝載工況比例。

結果表明：采用新提議的方法后，小尺度船舶第一層判定敏感的裝載工況比例有所增加。所有裝載工況的第一、二層衡準校核結果均維持一致，一致性問題得到了顯著改善。相關結果已提交IMO工作組討論[14]。

3.3 用于穩性直接評估計算方法的精度驗證指標

自SDC 4次會議起，直接計算衡準流程指南的制定被列為本議題工作最高優先級，以美國在SDC 1會議提議文本為基礎，完成了指南草稿文本的起草工作，以待進一步討論和修改。該指南的編制思路是針對5種失效模式分別給出數值軟件必須考慮的運動自由度和受力、環境條件設定以及數值模型精度的定性和定量要求。其中，最為核心的是針對數值模型精度的定性和定量研究。針對參數橫搖、純穩性喪失、過度加速度和騎浪/橫甩失效模式的穩性直接評估數值模型進行樣船計算研究，通過與模型試驗精度的對比分析，針對計算精度的定性和定量要求提出對應的建議[15-18]，用于進一步制定衡準流程指南草案。

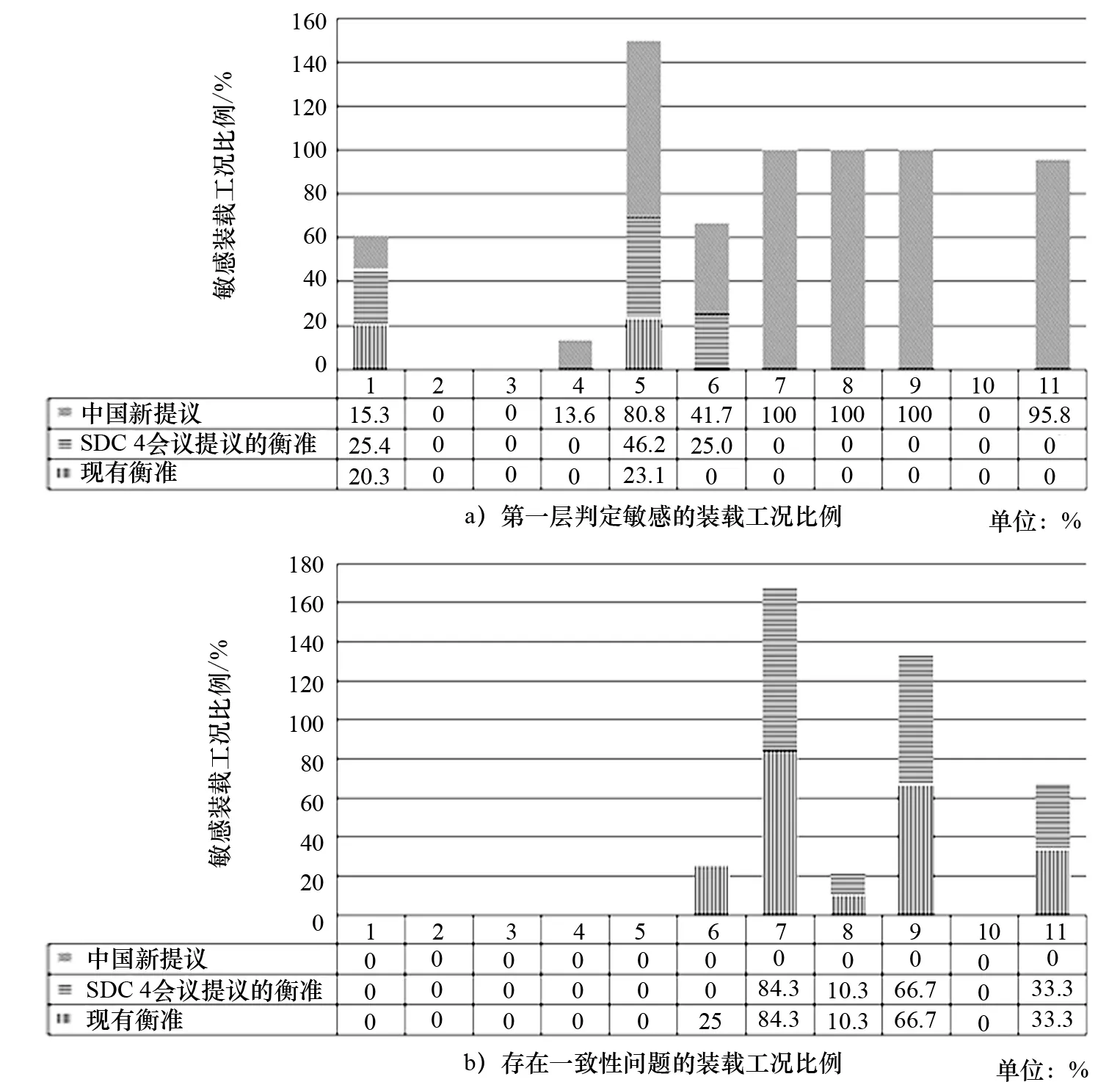
圖6 改進方案有效性比較

例如，針對參數橫搖穩性直接評估，采用3艘樣船的模型試驗結果用于進一步的驗證研究，包括2艘集裝箱船(10 000TEU和4 250TEU)和1艘滾裝船。分析混合方法的數值模擬精度和局限性。還分析混合方法的潛在缺陷，其中部分缺陷已通過采用全非線性計算流體力學(CFD)方法開展對比研究得到初步驗證。根據收集到的經驗，提出針對直接計算衡準流程指南草案定性精度指標的若干建議。部分船模的照片和數值模擬計算結果如圖7～圖9所示。指南草案主要針對橫搖幅值提出預報精度要求，因此，主要對數值預報獲得的橫搖幅值與模型試驗結果進行對比。在10 000TEU集裝箱船計算的19個算例中，15個滿足指南草案對于橫搖幅值的精度要求，即當橫搖幅值小于靜水GZ曲線最大值橫傾角時，誤差應小于10%橫搖幅值。

圖7 4 250TEU集裝箱船的參數橫搖現象

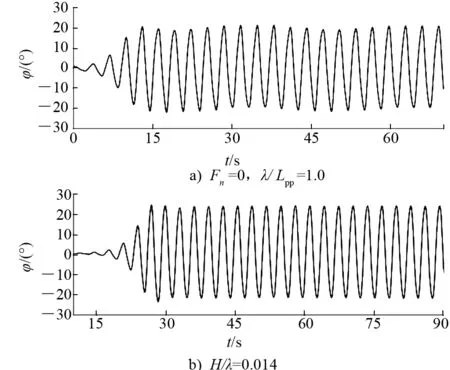
圖8 10 000TEU集裝箱船參數橫搖幅值預報結果

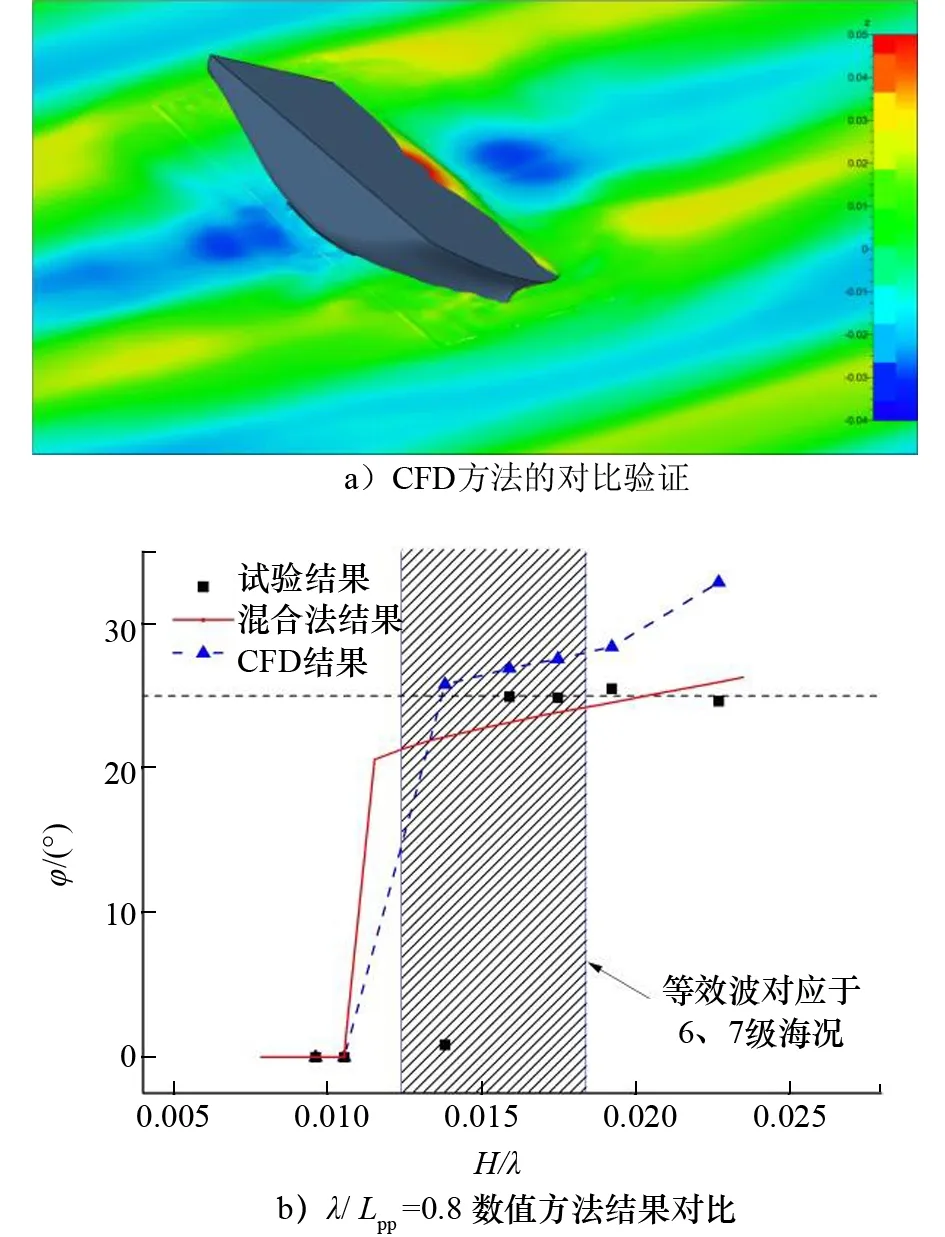
圖9 基于CFD方法的數值方法橫向比較 (10 000TEU集裝箱船)

4 結 語

在最近兩屆的SDC會議上，中國代表團以樣船計算和模型試驗等為技術支撐，針對第二代完整穩性衡準開展了大量基礎性研究工作，主要涉及參數橫搖Level 2衡準運動預報方法的選型研究、參數橫搖和純穩性喪失薄弱性衡準一致性檢驗研究、純穩性薄弱性衡準的一致性改進研究和用于穩性直接評估計算方法的精度驗證指標研究等方面。根據上述研究成果，總計提交了9份提案文件和4份信息文件，對于薄弱性衡準的改進和穩性直接評估指南的制定向IMO提出了大量建議。

根據IMO對第二代穩性研究的工作計劃和取得的進展，結合中國在船舶第二代穩性研究方面所取得的成果和技術水平，建議將以下幾方面作為未來工作的重點研究方向：

(1) 通過擴大樣船計算，進一步檢驗薄弱性衡準的一致性，積累對第二代穩性衡準敏感性水平的船型數據。

(2) 繼續研究純穩性喪失薄弱性衡準的適用條件。

(3) 繼續針對純穩性喪失薄弱性衡準的一致性問題開展研究。

(4) 開展更多的關于參數橫搖、過度加速度和純穩性喪失穩性直接評估方法的實船計算和試驗對比驗證研究，積累使用經驗。

(5) 加強針對實船操作指南/操作限制指南制定方面的研究，結合實船商業運營的經驗，制定相關指南文件。