由覆杯實驗引申的壓強問題研究

莊 黨，張 帆，張立娜，胡君輝，杜 婧，全文文，陽 麗

(廣西師范大學 物理科學與技術學院，廣西 桂林 541004)

在初中物理實驗中，覆杯實驗因為取材方便、操作簡單、現象直觀一直被用作驗證大氣壓存在的演示實驗. 將玻璃杯裝滿水，在杯口蓋1張紙，然后倒置，可以發現水被紙片托住. 實驗時，一般認為玻璃杯一定要裝滿水，不然實驗就會失敗[1]. 在實際教學中發現，有些學生在不裝滿水的情況下，同樣的方法倒置依然可以托住水. 為此，本文針對該問題展開了分析.

1 實驗模型

圖1(a)是實際做實驗過程中，觀察到的實驗現象：液面上方會有凹層，而在液面和紙張接觸處會有1層水層. 根據圖1(a)，可以做如圖1(b)所示的實驗模型圖來討論.

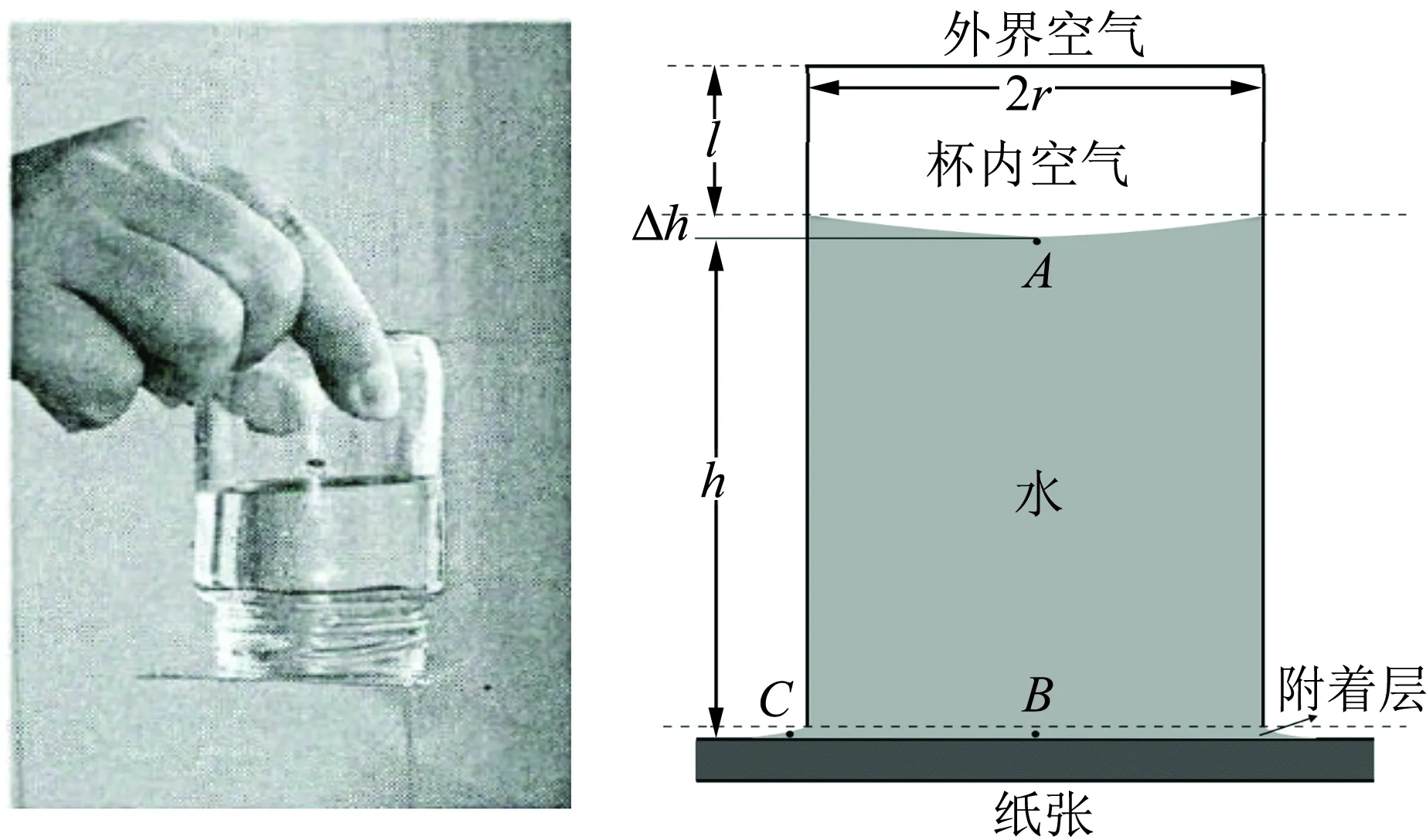
(a)實物實驗 (b)模型 圖1 覆杯實驗

1.1 液面附加壓強

由圖1(b)模型可知，紙張和水杯之間形成附著層. 液面下降的原因不是因為附著層，若不考慮附著層，不妨設下降高度為Δh，此時液面上部形成凹層. 由于Δh非常小，且下降的水全部分散于附著層內，因此可以認為水的高度h不發生變化. 液面上方形成的凹面. 因為弧度非常小，可以認為此凹面是半徑為X的球體的一部分，如圖2所示. 液塊受到3部分的力作用：1)通過液塊邊線作用在液面的張力；2)由底部作用于液面引起的附加壓強所導致的壓力；3)液塊受到的重力，與前兩部分力相比，小得很多，可忽略不計[2].

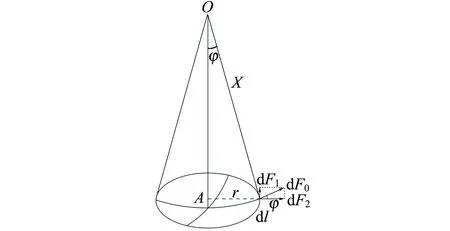
圖2 液體凹面受力示意圖

通過邊線每一微段dl作用在液體表面的張力dF0=αdl，可以分解成垂直于底面的分力和平行于底面的分力：

dF1=dF0sinφ=αdlsinφ,

(1)

dF2=dF0cosφ=αdlcosφ.

(2)

這兩部分力中，平行于底面方向的各個分力dF2由于方向都垂直于軸線OA，由對稱性可知，其合力為零；而垂直于底面方向的分力dF1，方向相同，合力大小為

(3)

根據平衡條件，液面下表面受到的力源于液面上下的壓強差[3]，即F1=Δpπr2，于是可以得到凹面的附加壓強[2]為

(4)

1.2 紙張和附著層的平衡條件

在此模型中，紙張能夠被吸附，是因為紙張和液塊分別滿足了平衡條件. 在紙張和杯子之間會形成液體的附著層，如圖3所示. 由于液塊自身的重力非常小，可忽略不計. 因此，液塊受到的力可以分成2部分：一部分是由于紙張的重力所引起的拉力F,另一部分是液體內部給小液塊的力. 液體內部的力又可以分為3個區域:附著層內部Ⅰ、液體內部Ⅱ和表面層內部Ⅲ. 區域Ⅰ作用的力是沿著紙張表面的壓力N，區域Ⅲ作用的力是水的張力T, 區域Ⅱ作用的力的大小與T和N相比太小可以忽略不計. 因此附著層的小液塊受到的力分別為N,F和T.

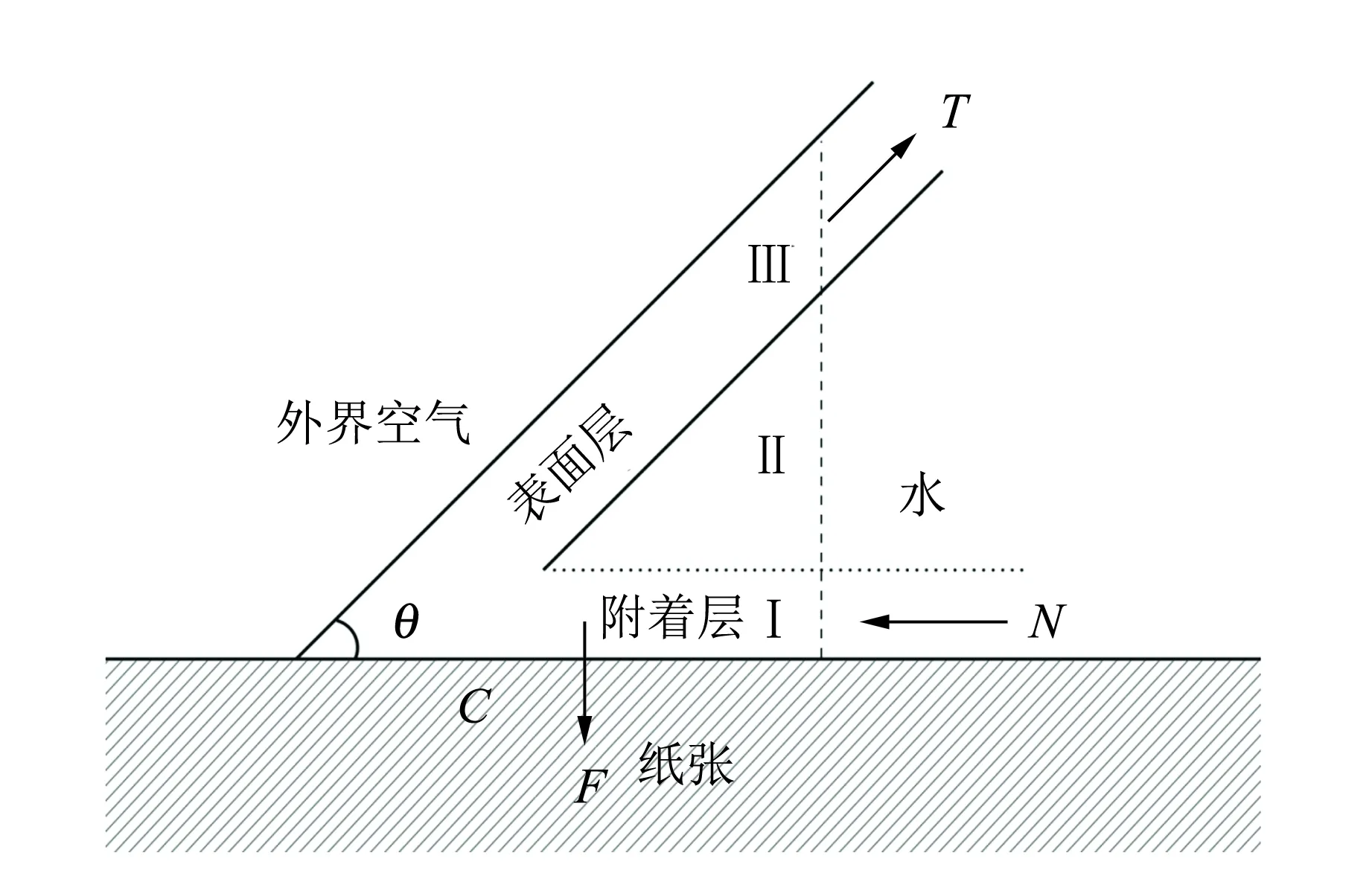
圖3 附著層與紙張受力示意圖

由平衡條件可以得到，

Tcosθ=N,

(5)

Tsinθ=F.

(6)

由(5)～(6)式可知，決定平衡的條件為：液體的張力、接觸角θ以及紙張的重力[3]. 液體的張力T由液體本身的性質決定，接觸角θ由液體和紙張的相對性質決定，對于給定的液體和紙張，接觸角θ是確定值. 因此，要使實驗現象得以實現的前提，取決于覆蓋物的質量m以及液體與覆蓋物的本身屬性.

2 杯內水柱平衡條件

由圖3可知，在杯子沒有被倒置之前. 杯內的空氣體積為V，當杯子被倒置時，液面會形成凹面. 此時杯內的空氣體積將會變大，而增加的體積是以X為半徑高為Δh的球冠，其大小為

(7)

倒置之后，杯內空氣體積為V1=V+V0. 根據氣體的物態方程[4]

pV=nRT=K,

(8)

式中，p為氣體壓強，V為氣體體積，n為氣體分子數，R為普適氣體常量.

2.1 支撐水柱的壓強分析

根據實驗過程可知，在倒置前后，溫度的變化可忽略，分子數并未發生改變[5]，因此K為常量. 此時，杯內空氣的氣壓值為

(9)

外界大氣壓值為

(10)

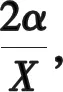
(11)

A點與B點的高度差為h. 此時，B點的壓強為

(12)

根據流體靜力學的基本原理，流體靜止時等高的兩點的壓強相等. 忽略紙張厚度，即pC=pB=p0，于是有

(13)

由(9)式～(10)式和(12)式～(13)式可以知道水柱高度與壓強的關系

(14)

由(14)式可知，支撐起水杯中水柱的原因為：彎曲液面內外的壓強差及由于杯內空氣與外界大氣的壓強差[6].

2.2 水柱平衡的實際數據分析

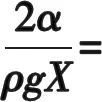
(14)式中后面部分，由(8)式可得

(15)

對于(15)式中，由于球冠的體積邊緣較小，可以近似認為它的體積是以半徑為r、高為Δh的圓柱的體積[6]，即

(16)

由此(15)式可以化解為

(17)

實際實驗中，l的高度約5 cm，假設Δh的高度為1 mm，綜合(14)式和(17)式可以得到，杯內空氣與外界大氣的壓強差能夠支撐起的水柱高度為20.2 cm. 可見，這是撐起水柱的主要原因. 1標準大氣壓可以支撐起10 m左右的水柱，而該實驗的水杯高度不會超過0.1 m. 由(17)式只要增加的凹面的體積不超過原有體積1%，形成的壓強差就可以支撐起水柱[7].

3 實驗驗證

3.1 實驗材料與實驗方法

實驗材料：普通玻璃杯1個(高13.5 cm)，不透水卡片1張，自來水. 為了清楚地看到玻璃杯內的空氣柱長度，在玻璃杯壁上標刻度.

為了演示玻璃杯中空氣柱的高度不會影響“覆杯實驗”的成功，分別進行了9組實驗，分別控制水柱的高度為玻璃杯的1/16，1/8，2/8，…,直到整杯水[8].

3.2 實驗現象

分別拍攝1/16,1/8,2/8,3/8,4/8,5/8,6/8,7/8以及滿杯水9種情況下覆杯實驗的演示現象,如圖4所示. 以上該實驗均獲得成功，由式(14)和(17)也可知杯內空氣與外界大氣的壓強差能夠支撐起的水柱高度為20.2 cm，在此實驗中即使滿杯水也未超過20.2 cm. 同時，1標準大氣壓可以支撐起10 m左右的水柱，在實驗中遠遠沒有達到10 m高度，且每次增加1/8的水量帶來的凹面體積的增加并未超過原有體積的1%. 因此，在實驗中液面高度的變化并不影響覆被實驗的成功.

(a)裝滿水 (b)7/8杯水 (c)6/8杯水

(d)5/8杯水 (e)4/8杯水 (f)3/8杯水

(g)2/8杯水 (h)1/8杯水 (i)1/16杯水圖4 不同水位的覆杯實驗

4 結 論

探究了未裝滿水的水杯能托起水柱的原因. 實驗結果表明：液體的張力、接觸角以及覆蓋物的重力決定了紙張和附著層的平衡條件，滿足平衡條件是此實驗實現的前提，能支撐起水杯中水柱的原因是彎曲液面內外的壓強差和杯內空氣與外界大氣的壓強差，而杯內空氣與外界大氣的壓強差是托起水柱的主要原因.