論數學教學中如何體會圖形運動思想并領悟其中獨特妙用

◆李春燕

(山東省濱州市濱城區第四中學)

數學思想方法是數學中的精髓，是聯系數學中各類知識的紐帶.掌握這些思想方法，將使人終身受益.圖形運動的思想在初中數學中，一般指圖形的平移、對稱、和旋轉三種.對稱包括軸對稱和中心對稱.在操作中，軸對稱常以翻折形式出現，中心對稱是旋轉角為180°時的旋轉運動.點的運動問題也體現了圖形運動的思想.

首先要熟悉各類圖形運動后產生的性質.運動后的圖形與原圖形是全等形；平移后的圖形與原圖形對應線段平行且相等，原圖形上的每一點都沿同一方向移動了同一距離；若兩個圖形關于某直線成軸對稱，則這兩個圖形上對應點的連結線段被對稱軸垂直平分，對應線段或互相平行或它們所在直線的交點必在對稱軸上；若兩個圖形關于某點成中心對稱，則這兩個圖形上對應線段互相平行且相等，對應點連結的線段都通過對稱中心，且被對稱中心平分；旋轉運動中，注意旋轉中心，旋轉方向和旋轉角.

解幾何題時，由于條件分散，相關圖形又不集中，很難發現量與量之間的關系，此時，將圖形進行平移、對稱、旋轉變換，將分散的條件集中起來，或置于某一熟悉的圖形之中，以改變問題情景，發現和運用某些特征、性質或聯系，由此找到問題的突破口和解決問題的關鍵，從而使原有問題得到解決.

這類問題的解題關鍵在于如何“化動為靜”，“以靜制動”，如何化繁為簡，化分散為集中，化難為易，體現“以不變應萬變”的核心規律.以下通過實例來滲透，理解，把握，體會，進而達到舉一反三，熟練運用.

例1：如圖，梯形ABCD中，AD∥BC，且∠C=90°-1/2∠B.求證:AB=BC-AD.

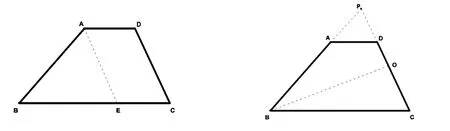
簡解：1.利用平移.將線段DC沿DA方向平移到AE，其中點E在邊BC上.則AECD為平行四邊形，∠DAC=∠AEB=∠C，AD=EC.又∠C=90°-1/2∠B，∴2∠C+∠B =180°，又∵∠DAB+∠B==180°∴∠BAE+∠EAD+∠B=∠BAE+∠C+∠B=180°，∴∠BAE=∠C=∠AEB，∴AB=BE=BC-EC=BC-AD.

2.常規解法.延長BA交CD的延長線于點P.過點B作CD邊的垂線，垂足為點O.利用已知條件證得△BPC與△APD皆為等腰三角形，進而證得結論.

點評：比較兩種證法，前者利用平移變換，將已知條件集中一個三角形中，到化繁為簡，求解十分方便，體現了運動思想解題的優越性;而第二種解法過程較復雜，煩瑣.

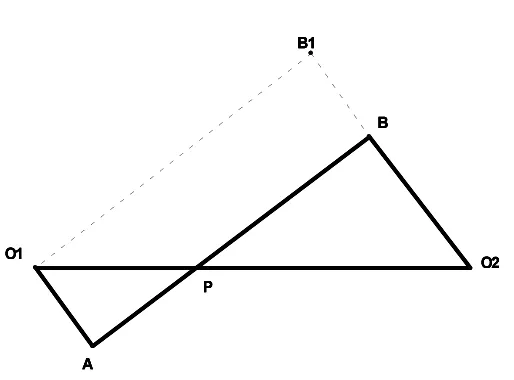
變式訓練：如圖，線段01O2與線段AB相交于點P，且01A⊥AB，O2B⊥AB，已知01A=r，O2B=R，01O2=d，(R、r、d均為常數).試求線段AB的長.

提示:利用平移，將AB平移到O1B1，將已知量R、r、d都集中在Rt△01O2B中，易求得AB即O1B1的長.(而利用平行線分線段成比例定理和方程思想，求得O1P、O2P的長，再利用勾股定理求得AP、BP的長，進而求得AB的長卻很煩瑣.)

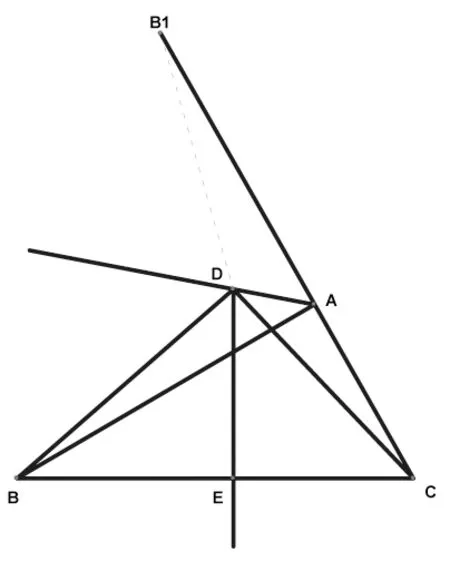
例2：如圖，△ABC中，BC的垂直平分線交∠BAC的外角平分線于點D，連結DC 、DB.求證:∠DBA=∠DCA.

簡解:將△BAD沿AD翻折到△B1AD，∵DA平分∠BAC的外角，∴AB1線在CA的延長線上，∴△ABD≌△AB1D，∴BD=B1D，且∠DBA=∠D B1A

∵DE垂直平分BC，∴DC=DB，∴DC=DB1，∴∠D B1A=∠DCA.因此，∠DBA=∠DCA.

點評：此題直接證∠DBA=∠DCA非常困難，而通過翻折(周對稱運動)，使∠DBA=∠D B1A，且∠DB1A與∠DCA在同一個三角形中，又是等腰三角形，因而得到∠DBA=∠DCA.本題通過運用圖形運動思想，找準問題的切入點，化難為易，妙筆生花，殊途同歸，不失為一典范好例.遇中點或中線考慮，作軸對稱圖形，也是常用輔助線之一.

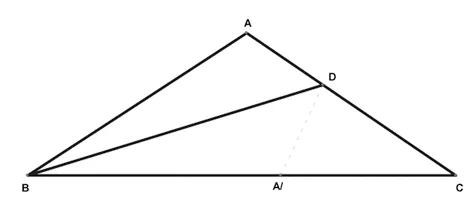
變式訓練：已知:△ABC中，AB=AC，∠BAC=120°，BD平分∠ABC，且與AC交于點D.求：AD:DC的值.

提示：將△ABC沿BD翻折，使點A落在BC邊上A1點，此時△DA1C是直角三角形.運用30°角對的直角邊是斜邊的一半，進而得出結論.

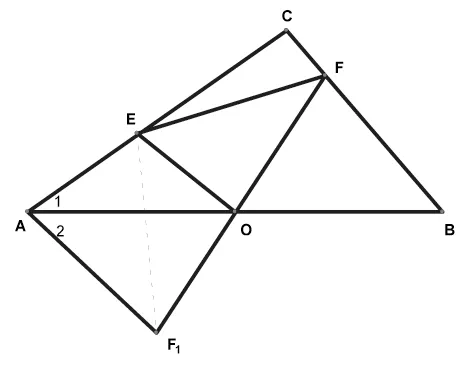
例3：如圖，△ABC中，∠C=90°，O是AB的中點，將三角尺的直角頂點置于點O，并繞點旋轉，使直角尺的另一邊交邊AC于E，直角尺的另一邊交邊BC于F(E、F均不與A、C、B重合)，連結EF.試問：三條線段AE、EF、FB是否總能構成一個直角三角形？請做出判斷，并證明你的結論.

簡解：三條線段AE、EF 、FB總能構成一個直角三角形，且EF是斜邊，最長邊.將△BOF繞點O旋轉180°至△AOF1，(即作出△BOF關于O點的中心對稱圖形△AOF1)，連結AF1，∵AF1=BF，∠2=∠B，∠ACB=90°，∴∠1+∠2=90°.即∠EAF=90°.∵EO⊥FF1，且F1O=FO，∴EF1=EF.

又△AEF1是直角三角形，有AE2+AF12=EF12，即AE2+BF2=EF2，∴AE、EF、FB總能構成一個直角三角形，且EF是斜邊，最長邊.

點評:此題是一結論開放性題，由于三線段AE、EF、FB較分散，通過圖形的中心對稱運動，使它們集中于一個AEF1中，而此三角形恰好是直角三角形，從而證明AE、EF、FB總能構成一個直角三角形，且EF是斜邊，最長邊.由此看來，將分散條件集中，是圖形運動思想在解題中的獨特妙用.

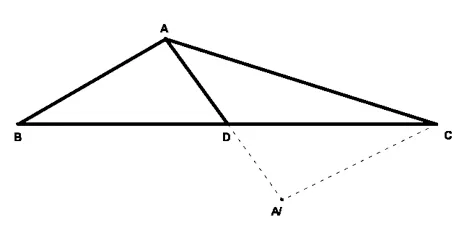
變式訓練：已知:△ABC中，AD是BC邊上中線，且AD⊥AB，AC=10，AD=4.求:邊BC的長.

提示：作△ABD關于點D的中心對稱圖形△A1CD，則△AA1C是直角三角形，由勾股定理得A1C=6，再由Rt△A1CD，求得DC，最后得BC=2DC.進而求得結果.

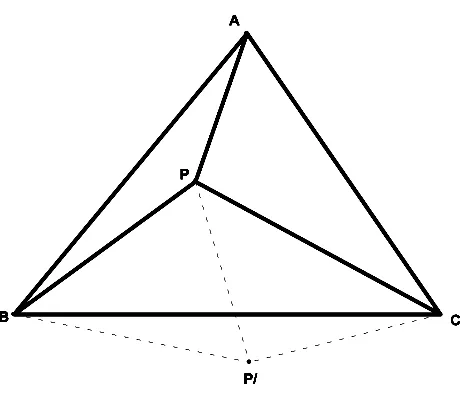
例4：已知點P是等邊三角形ABC內一點，∠APB=150°，PA=3，PB=4.求PC的長.

簡解：將△APB繞點B順時針旋轉60度，連結P P′.

因△ABC是等邊三角形，故△APB與△CP′B全等.BP=B P′，∠PB P′=60°.則得△PB P′為等邊三角形，BP′=BP=4，P′C=PA=3.

∴∠PB P′=60°，P′P= BP=4.又∵∠APB=150°∴∠P P′C=90°.在Rt△PP′C中，由勾股定理得PC=5.

點評:此題所求線段PC與已知線段PA、PB構不成一個三角形，條件分散，不易求解.由于△ABC是等邊三角形，具備旋轉角60°的旋轉條件，因此可作旋轉運動，將已知條件集中到一個直角三角形中，便于求解.此題解法新穎，充滿魅力.

變式訓練1：如圖，Rt△ABC中，∠ABC=90°，AB=3，BC=5，

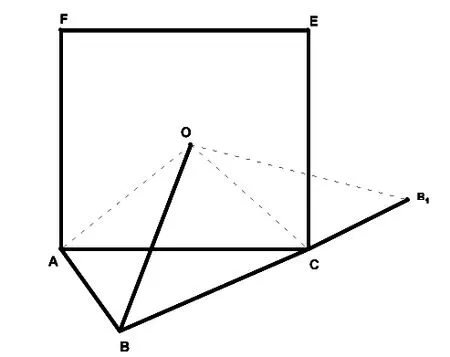
以AC為邊向△ABC外作正方形ACEF，設O為正方形ACEF的中心，連結BO.求BO的長.

提示：連結AO、CO.將△OAB繞點O逆時針旋轉90°到△OCB1，可證∠OC B1=∠OAB，點B、C、B1共線，進而證得△OBB1是等腰直角三角形，再求得BO長.

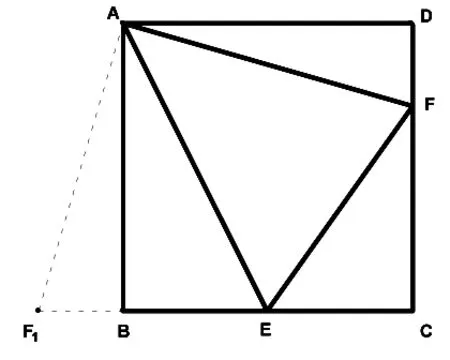
提示：將△ADF繞點A順時針旋轉90°到△ABF1，可證△AEF≌△AEF1，∠AEF=∠AEF1=60°進而求的EC、EF、EF1.將△AEF的面積轉化為△AE F1的面積.可為構思獨特.

將圖形運動的數學思想運用于數學實際，利用平移、對稱、和旋轉變換，尋求變化過程中的不變因素，抓住變換特征，研究內在聯系，找準突破口，將條件集中，數形結合，化難為易，化繁為簡，建立數量關系，就能達到動靜結合，以不變應萬變的核心目的.更會提升思維的高度，發展創新能力.