例談電子白板在“數形結合”思想滲透中的應用

張水仙

（古田縣第三小學，福建 古田 352200）

對于以具體形象思維為主的小學生來說，抽象的數學概念，嚴密的邏輯推理，嚴謹的數學語言等，確實有點枯燥乏味。生活經驗的欠缺，教學形式的單一，更是讓數學課堂沉悶無趣。“數缺形時少直覺，形缺數時難入微”[1]。如果能利用好具有融合傳統(tǒng)媒體，整合教學資源，為“互動教學而生”的電子白板，再運用“數形結合”的思想方法把蘊藏在例題、習題中抽象的數學語言與形象直觀的圖像結合起來，定能使復雜的問題簡單化，抽象的問題具體化，增強學生的學習興趣，為學生打下良好的數學思維基礎。

一、利用電子白板，“數形結合”幫助學生理解算理、掌握算法

在計算教學中，算理與算法是相輔相成，有機聯系的，算法是解決“怎么算”的問題，算理是解決“為什么這樣算”的問題。算理是計算的依據，是算法的基礎。利用電子白板，可以指導學生在理解算理的基礎上掌握計算方法，形成計算技能。

在學生動手操作的基礎上，教師可以借助白板畫圖的功能，邊評講邊拉出一個長方形，邊平均分邊涂色表示五分之一的三分之一，接著拋出第二個問題， 小時粉刷這面墻的幾分之幾呢？你能涂色表示 的 嗎？在學生回答的基礎上，請同學上臺涂色表示。

分數乘分數的計算法則和算理的教學，對六年級的學生來說，是比較抽象難以理解的，利用白板的涂色功能，通過兩次的動手操作，把抽象的算法借助“圖形化”的過程，學生直觀地理解了算理，最終得出了分數乘分數的計算法則，給學生留下了深刻的印象。

最后利用白板的思維導圖功能，再出幾道分數乘分數的題目，算式內容層層展開，讓學生進行口算，從而達到掌握算法的目的。

二、利用電子白板，“數形結合”幫助學生分析問題、解決問題

在小學數學教學中，解決問題類的知識占了很大的比重，求相差數問題，求倍數問題，連乘連除問題，借助線段圖找等量關系，并利用等量關系列方程解決問題。列表格尋找解決問題的策略、方陣圖、植樹問題等。在分析這些問題的數量關系時，無一不是由“數”聯系到“圖形”。利用電子白板，把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來，通過“以形助數”或“以數解形”使復雜問題簡單化，從而起到優(yōu)化解題途徑的目的，有助于增強學生的數學素養(yǎng)，提高分析問題和解決問題的能力。

例如，蘇教版四年下冊“用畫圖的辦法解決面積問題”。當長和寬同時增加或者減少，引起面積的增加或者減少，這類題目，學生往往很難想象的出來面積怎么變化。這時，利用電子白板，“數形結合”，通過畫圖演示，學生就能輕松地解決了這類問題了。

三、利用電子白板，“數形結合”幫助學生增強空間觀念，提高空間想象能力

空間觀念是在對周圍環(huán)境和實物的直接感知的基礎上形成的。小學生對于立體圖形和平面圖形的轉化，在一定程度上主要依賴于直覺觀察。因此，在教學中，教師要按照學生認識事物的規(guī)律，可充分利用電子白板，“數形結合”使學生獲得空間與圖形的鮮明表象，積累幾何圖形豐富的感性經驗。

在認識了圓柱的側面后，學生在頭腦中已經建立起一個封閉的、彎曲的表象。接著又要研究側面積，學生對于平面圖形和立體圖形之間的轉換，還有很大的困難，首先要解決的是化曲為直的問題，將圓柱的側面展開為一個平面的圖形（長方形或正方形）。在學生動手操作，剪一剪的基礎上，還可以利用電子白板“學科工具”中的圓柱體，通過“展開”功能，把圓柱就變成了各種類型的平面圖形，讓學生多方位地積淀對空間觀念的認識。

四、利用電子白板，“數形結合”增強學生學習興趣，提高課堂效率

電子白板集黑板、粉筆、PPT課件的功能為一體，構建起了新型的教學模式，教師根據學生和教材以及白板的特點，就能充分調動學生的興趣，提高課堂效率。

如蘇教版四年級下冊“三角形的內角和”。教材P113提供了三個三角形的素材，讓學生通過兩種方式：1.動手量一量，再把三個內角的和加起來，算出三角形的內角和是180°，這個方法有存在誤差的可能；2.折一折（撕下來或剪下來），再把這三個內角折一折或者拼一拼，得出了三角形三個內角的和是180°，這個方法得出的結論比較準確，可是，這三個三角形是課本指定的三角形，并不代表任意一個三角形的內角和都是180°。帶著這個疑問，教師可以利用白板“學科工具”中的三角形，請學生上來，任意畫一個三角形，白板強大的功能會立即顯示這個三角形三個內角的度數，學生只要把這三個內角的和加起來就能算出來了。因為有了學生自己畫的過程，以數畫形，學生們心服口服，不僅提高了學生的學習興趣，也提高了課堂的學習效率。（如圖）

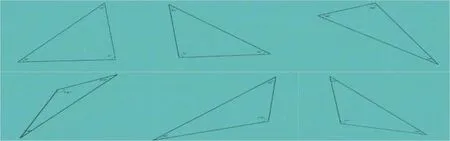
“千言萬語不如一圖”，[2]利用電子白板與“數形結合”教學，為師生的互動搭建了有利的平臺，既提高了學生的學習效率，又學得輕松愉快。當然，要想運用更加得當，必須先要了解電子白板的各種功能，操作要熟練，同時對哪些課題適合滲透“數形結合”思想也要心中有數，這樣才能因“材”施教，兩者交互，達到水乳交融的美好境界。