復雜結構條件下的動態組合維修決策模型研究

丁申虎，賈云獻

(陸軍工程大學石家莊校區， 石家莊 050003)

對于復雜裝備，組合維修決策主要根據部件之間的維修相關性。部件之間的維修相關性主要分為結構相關性、故障相關性和經濟相關性三類。經濟相關性是指多個部件同時進行維修比各部件單獨進行維修可以節省維修費用，是目前研究的熱點，本文也是基于經濟相關性對復雜裝備進行組合維修決策的研究。

目前研究比較成熟的是長期使用條件下復雜裝備的靜態組合維修模型，但在裝備的實際使用期中，維修信息很難一成不變，往往是動態變化的。受市場和環境條件的影響，維修的費用和部件的故障規律會呈現階段性的變化，維修人員數量的變化以及其他某種原因導致維修機會的出現，靜態維修策略往往忽略了這些因素對維修決策的影響，因此，Wildeman，Dekker等學者[1-3]開始做動態組合維修決策的研究。但是，大部分研究都假設系統中各部件是串聯關系，而實際上裝備系統的結構組成是很復雜的，各部件之間可能是串聯、并聯和橋路等，另一方面，這些研究都將預防性維修時間忽略不計。為了解決此類問題，本文針對部隊級維修中常見的成組更換工作，本文將綜合考慮復雜的結構關系和維修所花費的時間來建立成組更換的動態組合維修模型，從而進一步優化維修保量力量的配置。

1 復雜結構條件下的動態組合維修策略

復雜結構條件下的動態組合維修策略是綜合考慮了系統的結構關系和預防性維修時間，根據裝備在使用過程中出現的新情況，適時對維修計劃進行調整，以達到提高維修效率和節省維修費用的目的，這是一個不斷反饋和調整的維修決策過程。復雜結構條件下動態組合維修策略的基本思路是首先對系統結構進行分析，確定重要部件和重要組合，然后確定各部件單獨進行維修時的最優維修間隔期，接下來根據各部件的使用情況來確定初始維修計劃，按照費用最優的原則將各部件的維修計劃提前或推后使多個部件同時進行維修。最后，用滾動時域法，確定下一個使用期內的維修計劃，依次反復進行，復雜結構條件下的動態組合維修策略的基本流程如圖1所示。

1.1 符號說明

符號說明如下：

cpi:部件i成組更換時的特定預防性更換費用；

Cpi:部件i進行預防性維修的總費用；

Cfi:部件i故障后修復性維修的總費用；

S:部件i進行預防性維修和修復性維修需送修或聘請專業維修人員所產生的維修準備費用，為一定值且各部件均相等；

cd:重要部件進行預防性維修時單位時間的停機損失費用；

ij:部件i的第j次預防性維修；

tij:部件i進行第j次預防性維修的初始計劃時間；

tpi:部件i進行預防性維修所花費的時間；

Gk:第k個組合維修；

tGk:第k個組合進行預防性維修的時間；

DGk:對組合Gk中的部件同時進行預防性更換所花費的時間。

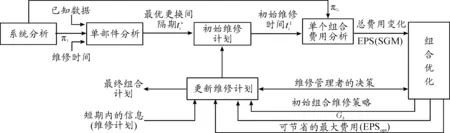
圖1 復雜結構條件下的動態組合維修策略

1.2 基本假設

裝備各部件均為單一故障模式，且各故障發生相互獨立；

部件在發生故障后進行修復如舊的維修，且修復性維修的時間忽略不計；

成組更換時的維修效果為修復如新；

系統停機進行維修活動時對部件的故障率不產生影響，即維修不會植入故障；

維修人員和備件充足；

各部件的故障規律服從尺度參數為ηi，形狀參數為mi的兩參數威布爾分布。

2 復雜結構條件下的動態組合維修決策模型

2.1 系統結構分析

通過分析系統的結構確定重要部件或重要組合。首先，用可靠性框圖描述系統的結構組成，并通過可靠性框圖中確定最小割集。最小割集表示能使系統發生故障的最少部件數，若最小割集中只含有一個部件，則這個部件即為重要部件。

若該部件為重要部件，則πi=1，否則，πi=0。如果由多個部件構成組合Gk中包含一個最小割集，那么組合Gk是一個重要組合，且πGk=1；若組合Gk不包含任何一個最小割集，則Gk是一個非重要組合，且πGk=0。

2.2 單部件優化

單部件優化是不考慮部件之間的經濟相關性，根據長期使用期下單部件的維修費用模型，確定各部件成組更換的間隔期。

在建模之前，我們要分析部件維修時的一些費用情況。當對部件進行預防新更換時，必須支付以下費用：

1) 維修準備費用S。主要為送修或聘請專業維修人員所產生的費用，為一定值且各部件均相等，且不管幾個部件同時進行維修時，所需花費的費用值都相等。

2) 特定的維修費用cpi。與部件的屬性有關，主要為購買所需的備件，特定的工具而產生的費用。

3) 對部件進行預防性更換導致系統停機時產生的停機損失。

因此，一個部件進行預防性更換的總維修費用為：

Cpi=S+cpi+πi·tpi·cd

(1)

式(1)中，

由于部件i的故障規律服從尺度參數為ηi，形狀參數為βi的威布爾分布，因此，部件i的故障率為：

(2)

用Mi(t)表示部件i在維修間隔期內發生故障的期望維修費用為：

(3)

由于部件的成組更換是一個更新過程，因此，在長期使用條件下,其單位時間內的期望維修費用可依據更新報酬理論得出，即

(4)

2.3 初始維修計劃

為了進行組合維修決策的研究，我們必須了解動態維修信息出現的時間及當前的維修現狀，以便進行下一步的分析和規劃。

定義t0表示現在的時刻，ij表示從t0開始，部件i的第j次預防性維修。根據單部件維修優化模型，從t0開始，部件首次進行預防性更換活動的時間為：

(5)

因此，部件之后各次預防性更換活動維修時機的關系為：

(6)

為了制定組合維修策略，我們要確定組合策略應用的時間范圍，起始點一般為當前時間t0，終止時間用tend表示，為確保在此之前所有的部件至少已經進行過一次預防性維修，因此

(7)

為了便于理解，在圖2展示了一個具有3個部件的系統的初始維修計劃。這里，若tbegin= 0，則tend=max(ti1+tpi)=t31+tp3，在這期間，部件2和部件3僅在t21,t31時進行一次維修，部件1在t11,t12時各進行一次預防性更換。因此，部件在此期間的預防性維修活動數N=4。

圖2 具有3個部件的系統的初始維修計劃

2.4 費用分析

假設組合Gk中含有nk個不同的維修活動，則這些維修活動會在tGk時同時進行。那么，這個組合產生的費用主要由以下四部分的變化構成。

2.4.1維修準備費用變化分析和因部件維修時間改變產生的費用變化分析

因為同時進行多個預防性維修僅需一次維修準備費用，所以組合Gk組合維修后可節省的維修準備費用為：

UGk=(nk-1)·S

(8)

由于組合維修，各部件的實際維修時間會比原計劃時間提前或推遲。組合維修后，維修活動ij的實際維修時間為：

tGk=tij+Δtij

(9)

(10)

圖3 部件i組合維修后的維修時間

一個組合內的部件因維修時間改變而產生的總費用變化為：

(11)

2.4.2預防性維修產生的停機損失費用變化分析

多個部件組合維修后，可以減小因預防性維修導致的停機時間。相比組合維修前，組合維修后因進行預防性維修而產生的停機損失的費用變化為：

(12)

(13)

(14)

由于維修人員和備件充足，多個部件組合后的系統停機進行預防性維修的時間為參與組合維修的部件進行預防性維修的最大值，即

(15)

式(15)中，πGk是一個指標函數，其定義如下

因此，組合維修后組合Gk因進行預防性維修所產生的停機損失費用變化為：

(16)

1) 當Gk是一個非重要組合，則πGk=0,組合中任何一個部件πi=0。

2) 當不考慮預防性維修的時間，則tpi=0,DGk=0。

2.4.3 總費用變化分析

通過以上三部分費用變化的分析，組合維修后單個組合實際的總費用變化情況為：

以上，我們僅給出了一個組合維修費用的計算方法，假設在[t0,tend]內的維修活動有N個，將這些預防性維修活動按照時間順序排列，可形成一個維修活動所構成的集合Gzong={1,…,N},集合Gzong可以看作是由互斥的組合G1,G2,…,Gm構成，即

Gj∩Gk=?, ?k≠j

G1∪…∪Gm=Gzong={1,…,N}

因此，結合系統中所有部件組合后可節省的費用為：

(17)

對式(17)進行求解，當節省的費用最大時，各部件所對應的維修時機和組合方式即為最優的組合優化方案。

2.5 更新維修計劃

通過以上分析，我們可以得到在有限時間[t0,tend]內所有部件的組合優化方案，但當前的時間區域是低于裝備的使用壽命的，等到了使用間隔期的末端，需重新確定系統中的部件在下一階段的組合維修方案。

但在實際的維修過程中，在[t0,tend]內的維修信息不是一成不變的，會有很多新情況出現，比如維修機會的出現、訓練任務發生變化、系統的結構發生變化等，這樣當前的組合維修方案并非最優，這就需要我們重新進行系統結構分析，制定初始維修計劃階段，確定一個新的維修時域，進行費用分析后，重新制定組合維修方案。接下來，若又有新的情況出現，再進行系統結構分析，制定初始維修計劃，確定一個新的維修時域，這樣反復進行以上步驟，由于維修時域是不斷變化向前的，這種求解方法也稱作滾動時域法，具體過程如圖4所示。

圖4 滾動時域法

3 案例分析

假設一個裝備系統由8個部件構成，系統的結構可靠性框圖如圖5。已知cd=80,S=100,各個部件的特定預防性維修費用、故障后修復性維修的總費用(元)、已工作時間(天)、預防性維修活動所用的時間以及壽命分布的形狀和尺度參數如表1所示。

表1 系統中各部件的相關參數

通過分析系統結構可靠性框圖，我們可以發現該結構共有6個最小割集，分別為：組合只要包含其中的一個最小割集，那么該組合即為重要組合，同時，我們可以看出各部件是否為重要部件，各部件的值如表2所示。

首先，根據長期使用條件下單部件的維修決策模型，結合式(1)、(4)、(5)知，各部件預防性維修總費用、最優預防性維修間隔期、單位時間的期望維修費用和部件首次進行預防性維修的時間如表2所示。

圖5 系統的結構可靠性框圖

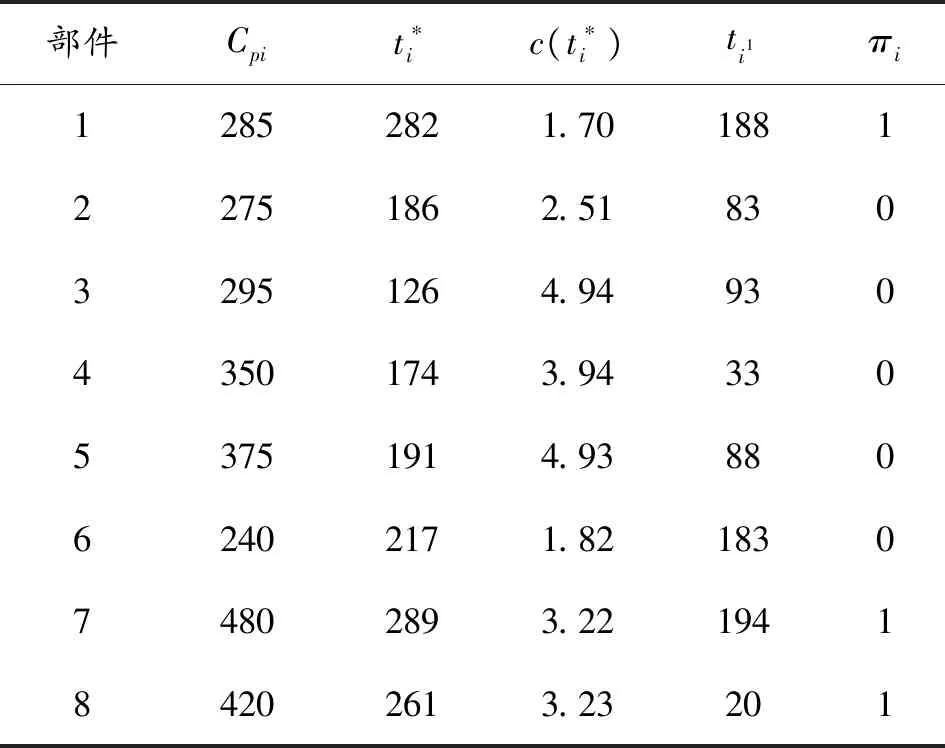
部件Cpit?ic(t?i)ti1πi12852821.70188122751862.5183032951264.9493043501743.9433053751914.9388062402171.82183074802893.22194184202613.23201

根據各部件首次預防性維修情況，可以得出組合維修的使用范圍為t0=0,tend=t71+tp7。根據公式(6)，我們可以得出各部件其他次維修的時機，但他們的時間已經超出了[0,195]的范圍，這就意味著，每個部件在此期間僅進行了一次預防性更換工作，各部件的初始維修計劃如圖6所示。

圖6 系統中各部件的初始維修計劃

在間隔期內，按照單部件維修策略，各個部件單獨進行維修時所需花費的期望維修費用為：

依據組合維修策略模型，運用遺傳算法工具箱進行求解，優化過程如圖7所示，最終，可得系統組合維修后可節省的最大維修費用為498.125元，相比組合前大約節省了的維修費用，具體的維修計劃如表3所示。

圖7 優化過程

組合部件pGktpGktGkP(Gk)G14,8132899.336G22,3,50390199.346G31,6,712191199.443

表4 組合維修計劃更新后的和ti1數值

表5 考慮維修機會后的組合維修計劃

同理，各個部件單獨進行維修時，所需花費的期望維修費用為:

組合維修后，可節省的最大維修費用maxP(Gzong)=588.942，比組合前節省了15.23%的維修費用，說明利用維修機會對組合維修策略進行調整,可有效地節省維修費用。

5 結論

本文將動態組合維修策略應用到非串聯結構條件下的復雜裝備的研究中，綜合分析了系統結構和維修時間兩個因素的影響，更貼近復雜裝備的維修現狀，具有很強的現實意義。但本文組合維修的依據僅考慮了部件間的經濟相關性，對于部件間結構相關性和故障相關性時的組合維修策略，還需進一步深入研究。