基于Abaqus的齒輪傳動系統模態分析

鄭 巖，李 穎

(1.吉林省建研科技有限責任公司，吉林 長春 130000；2.長春理工大學，吉林 長春 130000)

1 引 言

齒輪傳動系統是由齒輪、轉子和軸承等組成的傳動系統，研究其動力學特性就是為了確定和評價齒輪傳動系統的動態性能，找出導致系統振動超限的因素，并進行優化，同時也為設計高質量的齒輪傳動系統提供理論上的指導。

齒輪傳動系統的固有特性是指固有頻率以及相應的振型，是其最基本的動態特性之一，對系統的動載及振動形式等均有顯著的影響。對于齒輪傳動系統固有特性的研究，目前最為有效的方法是基于有限元法的模態分析[1-3]。

2 模態分析基本理論

物理參數分析模型通常為多個廣義坐標相互耦合的二階常微分方程組，這種微分方程組不易求解。通常采用坐標變換的方法，使方程組解耦，成為一組以模態坐標及模態參數描述的非耦合方程，以便于對其進行求解，這種方法即為模態分析法。坐標變換矩陣為模態矩陣，其每列為模態振型。模態分析中，采用了模態截斷的處理方法，可以很大程度地減少方程數目和計算容量，計算成本較低[4-5]。

時域和頻域內均可采用模態分析法，其目標是提取系統的模態參數，為系統的振動特性分析以及結構動力學特性的優化、設計等提供依據。

對于多自由度無阻尼自由振動系統，其運動方程為：

(1)

此系統中存在N個固有頻率及對應主振型，每一對固有頻率和振型代表一個單自由度自由振動系統。這種在自由振動時結構所具有的基本振動特性即為結構的模態。多自由度系統的自由振動可以分解為N個固有模態振動的疊加。一般來說，多自由度系統是做多個固有頻率的簡諧振動的合成振動。

設多自由度自由振動系統中某一簡諧振動形式的解為：

(2)

則有：

(3)

將式(2)、式(3)代入式(1)，得出特征方程：

(4)

|([K]-ω2[M])|=0

(5)

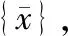
根據有限元理論，可得系統的分析模型：

(6)

[φ]=[φ1,φ2,φ3……,φn]

(7)

則有：

[φ]T[M][φ]=[I]

(8)

(9)

若設[C]=[0]，即對多自由度無阻尼振動系統，式(6)可化為：

(10)

式中，[φ]即模態矩陣，{Q(t)}=[φ]T{p(t)}稱為模態載荷列陣，[I]稱為模態質量矩陣，[Ω2]稱為模態剛度矩陣，[q]稱為模態坐標。

3 基于Abaqus的齒輪傳動系統模態分析

(1)啟動Abaqus/CAE導入分析模型

基于Creo4.0軟件的特征建模技術和參數化建模技術建立齒輪傳動系統的參數化模型，包括外嚙合直齒圓柱齒輪和軸的參數化建模。建立的齒輪傳動系統參數化模型見圖1，Abaqus/CAE模型文件導入界面和齒輪傳動系統運動簡圖如圖2、圖3所示。

圖1 齒輪傳動系統的參數化模型

圖2 Abaqus/CAE模型文件導入界面

(2)設置材料屬性

齒輪傳動系統齒輪材料選用高級優質合金結構鋼12Cr2Ni4A，材料參數如表1所示。

表1 齒輪傳動系統材料參數

(3)定義頻率提取分析

在分析步設置模塊，選擇Procedure type類型為“線性擾動：頻率提取”分析步，求解器類型選擇為Lanczos，在Number of eigenvalues requested后選擇Value，并輸入特征值數目20，默認其他選項，完成分析步設置。

(4)定義接觸

完成接觸屬性的定義，選擇“Hard”Contact，其他選項默認；并且在Contact Property選項卡中Global Property assignment指定為上步所創建的接觸屬性。

(5)施加邊界條件及載荷

在模態分析中，載荷對其沒有影響，只有邊界條件對系統有影響，所以僅施加邊界條件。施加邊界條件后使傳動系的各軸僅具有一個繞Z軸的旋轉自由度。圖4為齒輪傳動系統邊界條件的施加位置和方向。

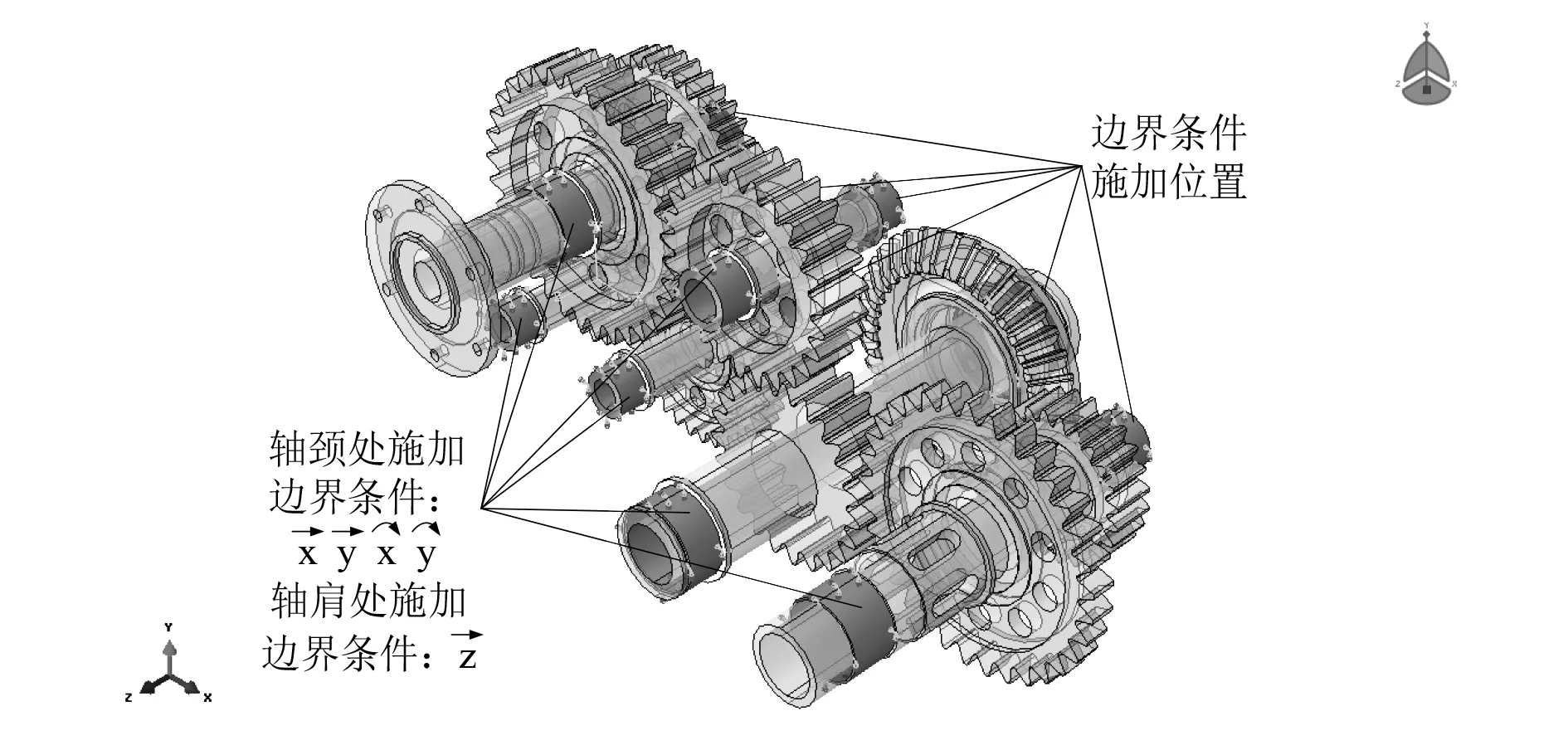
圖4 齒輪傳動系統邊界條件的施加位置及方向

(6)分網

進行網格劃分時，首先需要布種子，設置Approximate global size為5.0，單元類型選擇修正的二次Tet單元(C3D10M)，并選擇自由分網技術，網格模型如圖5所示。

圖5 齒輪傳動系統網格模型

(7)提交分析作業及后處理

采用Lanczos算法求解齒輪傳動系統前10階模態頻率及模態振型情況，見表2，圖6給出了齒輪傳動系統的前10階模態。

表2 齒輪傳動系統前10階模態頻率及振型

(a)第1階模態

(b)第2階模態

(e)第5階模態

(f)第6階模態

(g)第7階模態

(h)第8階模態

(i)第9階模態

(j)第10階模態

在忽略外部激勵對系統的影響，僅考慮含內部激勵作用的齒輪系統主共振響應特性的情況下，齒輪傳動系統的激勵頻率主要為嚙合頻率。齒輪傳動系統的嚙合頻率為P=nZ/60，其中，n為齒輪軸轉速(r/min)，Z為齒輪輪齒數目。現分別計算該齒輪傳動系統各級齒輪副的嚙合頻率，如表3所示。嚙合頻率遠離系統的前10階模態頻率(前10階模態最高模態頻率為2110.9Hz，見表2)，故附件傳動系統在嚙合頻率的激勵下不會產生圖6所示模態振型，所以不會發生共振。

表3 齒輪傳動系統各級齒輪副的嚙合頻率

4 結 論

針對試驗機等設備研究過程中常需要對齒輪傳動系統進行動力分析，借助Abaqus有限元軟件對齒輪傳動系統進行模態分析，是一種基于結構動力學的模態分析方法。雖然這種方法為大多數學者所采用，但是由于齒輪系統是高速旋轉件，而轉速對系統模態有很大影響，這種方法存在一定的誤差。本文基于結構動力學的模態分析，得到了附件傳動系統的前10階模態頻率及相應振型，在忽略外部激勵，僅考慮含內部激勵作用的齒輪系統模態分析的結果表明，齒輪傳動系統的嚙合頻率遠離齒輪傳動系統的前10階模態頻率，不會產生前10階模態振型，所以不會產生共振。

基于齒輪傳動系統中齒輪實體樣機，對其進行有限元模態分析。通過對齒輪傳動系統的參數化建模，調整模型參數，分析不同參數時齒輪傳動系統的動態性能，為齒輪系統的性能優化提供指導。參數化的齒輪系統模型還能在性能優化之后，根據相應的優化參數做出相應調整，為設計高質量的齒輪傳動系統奠定基礎。