變剛度轉臂定位節點對地鐵車輛車輪磨耗的影響

祁亞運， 戴煥云， 魏 來， 干 鋒， 徐 坤

(西南交通大學 牽引動力國家重點實驗室，成都 610031)

隨著我國軌道交通的迅速發展，地鐵運營里程逐年增加。載客量不斷增大，地鐵車輪磨耗問題日益顯著。地鐵線路一個重要特點是小曲線多，車輛啟動制動頻繁。因此地鐵車輪存在嚴重的磨耗，鋼軌也出現大量的波磨現象。關于地鐵車輪磨耗的問題，國內為學者十分關注這一問題。首先Pearce等[1-3]根據試驗提出了車輪磨耗模型，并確定了相關系數。Han等[4]根據實測車輪磨耗型面的擬合出了車輪磨耗模型并用于車輪磨耗預測取得了不錯的效果。Pombo等[5]利用多體動力學軟件仿真并用于車輪磨耗預測。Ignesti等[6]采用磨耗模型分析了鋼軌和車輪的磨耗。陶功權等[7]在考慮穩定性的基礎上進行車輪磨耗預測。羅仁等[8-9]探究了不同的系統參數對車輪磨耗的影響。于春廣等[10]對地鐵車輪磨耗進行了跟蹤測試，提出相應車輪減磨措施。陶功權等[11]從靜力學角度分析了不同軌底坡對我國常用于地鐵車輛的LM, 51002和DIN5573型面與CN60鋼軌匹配的輪軌接觸特性的影響。沈鋼等[12]對比初始與實測輪軌型面對上海地鐵A型車的曲線通過性能的影響，并分析不同的輪軌型面匹配對輪軌磨耗、鋼軌波浪形磨耗、接觸疲勞的影響。李霞等[13]介紹了車輪磨耗的預測方法。考慮輪軌動態接觸狀態，采用數值分析方法分析異常磨耗的地鐵車輪和新鋼軌作用情況，且對導致地鐵車輪踏而異常磨耗的原因作了分析。丁軍君等[14]在SIMPACK軟件中建立地鐵車輛動力學模型，基于FASTSIM算法和Braghin踏而磨耗模型，分析彈性滑動速度對磨耗的影響，并對車輛在直線、曲線和實際線路上運行時的車輪磨耗過程進行仿真。張隸新等[15]利用變剛度轉臂定位節點對車輛動力學的影響。孫宇等[16]研究了凹形磨耗下輪軌兩點接觸時的輪軌力和動力學性能。李國棟等[17]研究了LMB踏面長期磨耗狀況下其動力學性能和輪軌接觸關系的研究，最后表明LMB踏面延長了車輪磨耗里程，同時在磨耗周期內減弱了車輛振動。楊陽等[18]通過結合機車動力學仿真和Achard磨耗模型研究了不同牽引力矩對車輪磨耗的影響，同時與實測踏面數據進行對比。李亨利[19]主要研究了貨車車輪磨耗的規律和不同的影響因素。楊新文等[20]采用修正的非Hertz接觸算法計算了曲線超高對鋼軌磨耗的影響。

本文首先分析了變剛度轉臂定位節點模型的頻變特性和幅變特性，利用該模型的在曲線通過時的優勢，將其用于地鐵轉臂定位節點的磨耗仿真分析，計算了定剛度和變剛度轉臂定位節點在曲線通過時的受力。最后采用Zobory模型計算了地鐵車輛的通過不同線路狀況的磨耗深度，并進行了車輪磨耗預測分析以及模型參數對磨耗的影響。

1 模型建立

1.1 轉臂定位節點建模

轉臂定位節點是連接構架和軸箱機構的重要部件，一般是橡膠件。轉臂定位裝置如圖1所示。德國Freudenberg Schwab公司開發了具有變剛度特性的轉臂定位節點，變剛度轉臂定位節點模型考慮了其頻變特性，在直線上剛度大，表現為硬特性；在曲線上剛度較小，表現為軟特性，具有自適應的調節功能，改善了車輛的曲線通過性能。本節采用Poynting-Thomson模型(以下簡稱PT模型)模擬該變剛度定位節點的非線性特性。PT模型如圖2所示。其中包括2個彈簧單元和1個阻尼單元，彈簧與阻尼組成串聯單元，該串聯模型再和彈簧并聯組成PT模型。

圖1 轉臂定位節點裝置Fig.1 Rotary arm positioning node device

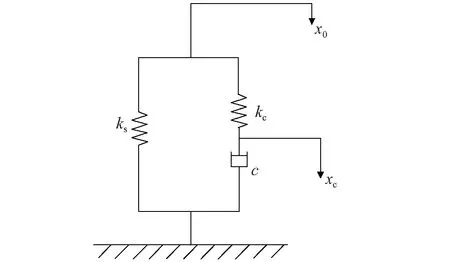
圖2 Poynting-Thomson模型示意圖Fig.2 Poynting-Thomson model schematic diagram

在PT模型中，x0=A0·sin(2πf·t)。 其中：A0為激擾幅值；f為激擾頻率。 串聯單元的力F可以表示為

F=ksx0+kc(x0-xc)

(1)

PT模型中的具體參數見表1。 從式(1)可知， PT模型中力與位移的關系，通過改變激擾頻率和激擾幅值，可獲得系統的非線性剛度和阻尼特性曲線。

表1 模型參數

圖3和圖4給出了PT模型的頻變特性和幅變特性曲線，從圖3可知，頻率增大后，示功圖斜率越大，說明剛度變大，示功圖面積變小，說明模型阻尼變小。從圖4可知，隨著幅值的改變，頻率不變，因此剛度不會增大。隨著幅值增大，示功圖增大，模型阻尼也增大。

圖3 模型頻變特性Fig.3 The frequency variation characteristics of model

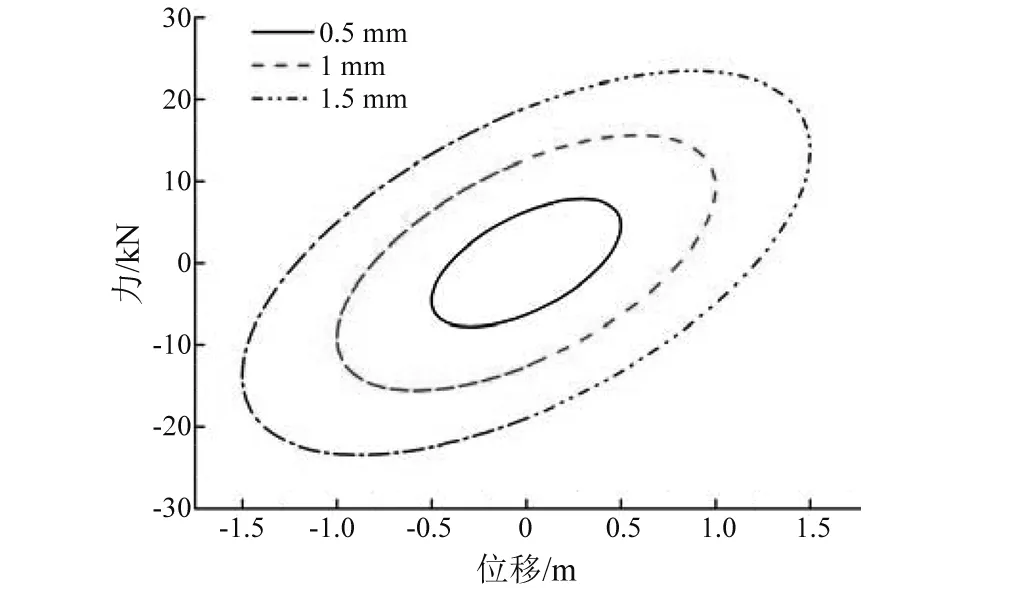
圖4 模型幅變特性Fig.4 The amplitude variation characteristics of model

仿真值和試驗剛度對比，如圖5所示。從圖5可知，試驗值和理論值有很好的一致性。模型準確地模擬了頻變剛度特性。因此將該模型用于變剛度轉臂節點仿真時有效的。

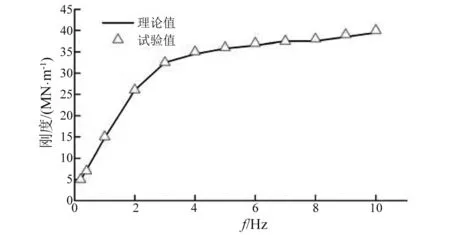
圖5 仿真計算和試驗剛度試驗值對比Fig.5 Comparison of simulation and test stiffness test values

1.2 車輛模型

建立我國地鐵車輛模型，采用LM踏面，選取1個車體，2個構架、4個輪對與8個轉臂以及一系懸掛和二系懸掛系統組成車輛系統。車體、構架、輪對考慮了縱向、橫向、垂向、側滾、點頭、搖頭6個自由度。輪對的垂向和側滾運動耦合在一起；轉臂只考慮點頭自由度，該模型考慮車輛自由度，如表2所示。以車輛前進方向為x軸，y軸為平行于軌道方向，z軸為垂直于軌道向下建立坐標系。車輛模型如圖6所示。考慮輪軌非線性的接觸關系和車輛懸掛系統，車輛系統的動力學方程表示為

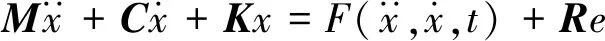
(2)

表2 車輛自由度

圖6 車輛動力學模型Fig.6 Vehicle dynamics model

1.3 輪軌接觸算法

計算輪軌接觸特性時，選用Hertz-FASTSIM的的快速算法，即輪軌間法向力的計算采用Hertz接觸理論，切向接觸應用FASTSIM接觸理論。這種算法由Hertz接觸理論計算橢圓接觸斑大小，并在接觸斑內劃分網格單元，每個單元的長度為Δi和Δj。接觸單元上的法向力為

(3)

(4)

式中：pz(i,j)為接觸網格上的法向力分布；a，b為接觸斑長軸、短軸一半； Δv，Δvi，Δvj為相對滑動速度、縱向相對滑動速度、橫向相對滑動速度；vi為質點通過接觸點的速度。

并假設接觸斑內任意一點(i,j)的彈性位移u與同方向的法向力p和柔度系數L有關， 即：u(i,j)=L·p(i,j)，滑動方程描述為

(5)

式中：Vi，Vj為縱向和橫向滑動速度；Vv為列車運行速度；ξi，ξj為縱向和橫向蠕滑率；φ為自旋蠕滑率；u1，u2為縱向和橫向彈性位移。

彈性滑動速度可以表示為

(6)

黏著區和滑動區共同構成了接觸斑區域，磨耗主要發生在接觸斑內的滑動區。將接觸區進行劃分(見圖7)，假設切向力的大小與輪軌間的切向應變成線性關系。

u(i,j)=L·F(i,j)

(7)

式中：u(i,j)為彈性變形；L為柔度系數；F(i,j)為輪軌間的切向力。 柔度系數L可以利用KALKER理論中蠕滑力與蠕滑率之間的關系得到。

(8)

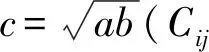
圖7 橢圓接觸斑示意圖Fig.7 Sketch of ellipse contact spot

接觸斑(長軸是2a，短軸長為2b)被劃分成i×j個接觸單元，單元格的長度分別為Δi和Δj，見圖2。任意單元內，滑動速度與剛性滑動量和切向變形有關，即

(9)

式中：vs(i,j)滑動速度；p(i,j)為剛性滑動量。

(10)

在黏著區域，滑動速度為0，左邊為0，切向力為

(11)

在滑動區域，根據庫倫摩擦定理： 當接觸斑單元上的切向力大于其最大摩擦力(輪軌法向力乘以摩擦因數)， 若F(i,j)≤Fmax(i,j)， 則單元格處于黏著區； 若F(i,j)>Fmax(i,j)， 則滑動出現，滑動區單元格切向力

(12)

1.4 ZOBORY磨耗模型

在ZOBORY磨耗模型中， 接觸斑劃分為nx×ny個單元格，由上節可知， 輪軌接觸區劃分為黏著區和滑動區，分別表示為Aa和As。 根據輪軌蠕滑理論，黏著區內不發生磨耗，只在滑動區發生磨耗。接觸斑內的磨耗能量流密度為

(13)

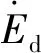
(14)

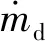
應用質量流密度計算單位面積的質量為

(15)

圖8 磨耗系數Fig.8 Coefficient of wear

由于接觸班劃分的網格塊很小，可以近似為

(16)

則磨耗深度可以表示為

Δz=Δm/(ρ·ΔA)

(17)

式中： Δz為磨耗深度；ρ為材料密度； 將式(15)代入式(17)就可以計算出接觸班上網格塊的磨耗深度。

2 變剛度模型動力學性能

2.1 變剛度模型曲線通過性能

為了計算變剛度模型曲線通過性能，采用500 m曲線半徑，超高為120 mm，速度為70 km/h。軌道激擾采用地鐵線路軌道激擾。分別計算了變剛度模型和定剛度模型的磨耗功、輪對沖角以及縱/橫向蠕滑力。

從圖9～圖11中可知，車輪通過500 m曲線時的車輪磨耗功、輪對沖角和蠕滑力計算結果，從圖中可以看出采用變剛度模型時的磨耗功比定剛度模型減小50%。采用變剛度模型時輪對沖角比定剛度模型減小55%，因此可以看出采用變剛度模型時曲線通過性能有了很大提升，而且減小了車輛通過曲線的磨耗；定剛度模型縱向蠕滑力最大值為13 kN，動剛度模型的縱向蠕滑力為5.5 kN。定剛度模型的橫向蠕滑力值為10 kN，變剛度模型的橫向蠕滑力為6 kN。變剛度模型使得縱向蠕滑力和橫向蠕滑力明顯降低。

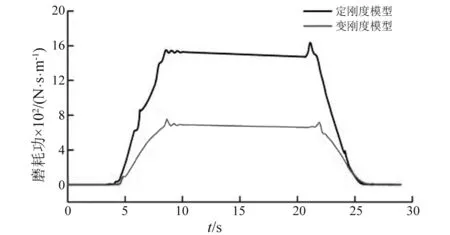
圖9 磨耗功Fig.9 Wear power

圖10 輪對沖角Fig.10 Wheelset angel

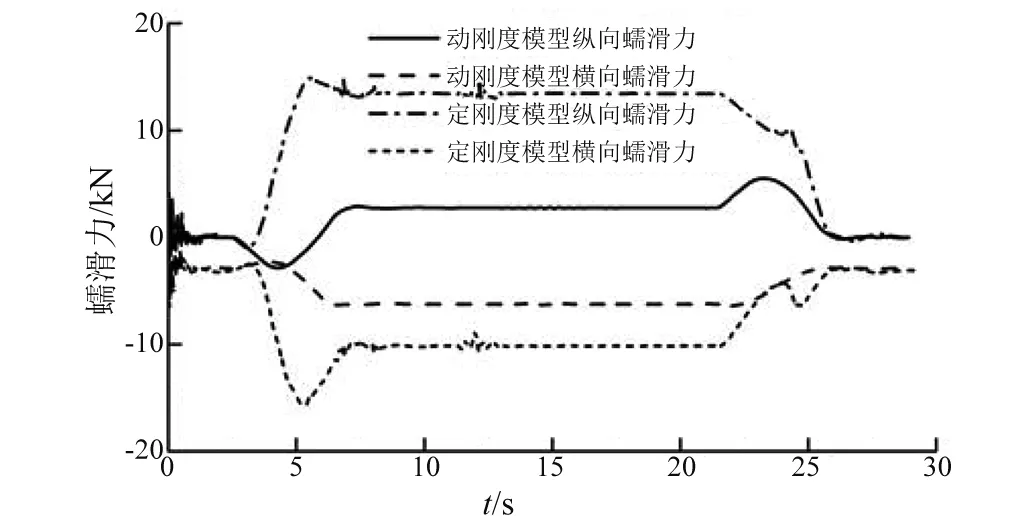
圖11 蠕滑力Fig.11 Creep force

2.2 變剛度模型平穩性和安全性計算

由上節可知，采用變剛度節點具有較好的曲線通過性能，但對于車輛的平穩性和安全性影響未知，本介計算了兩種模型下平穩性和安全性指標。

從圖12可知，采用動剛度模型時車體中部平穩性有所降低，當速度在100 km/h時，平穩性指標降低5.6%。從表3可知，采用動剛度模型時其輪軌橫向力和傾覆系數和定剛度模型差別較小，脫軌系數和輪重減載率都有了一定的減小，脫軌系數較小了10.2%，輪重減載率減小了9.3%。

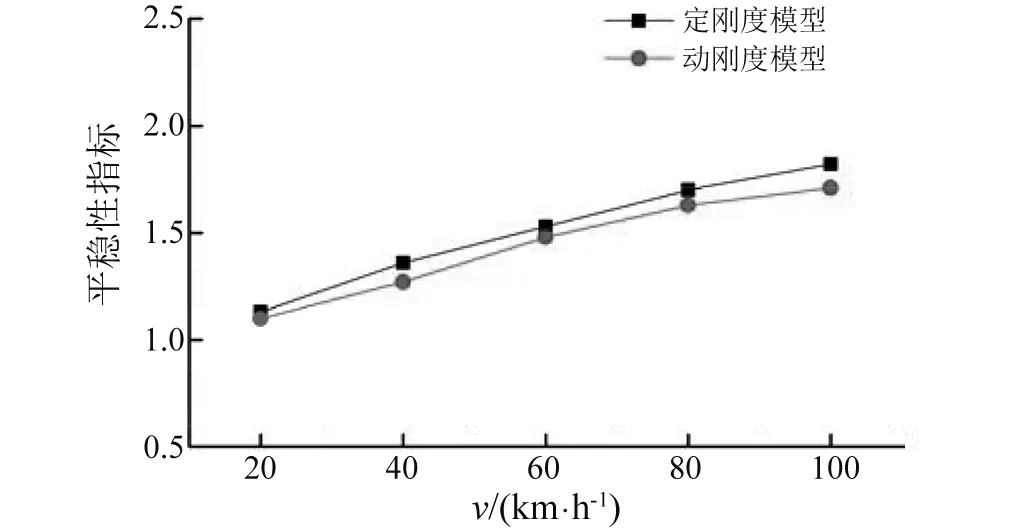
圖12 車體中部平穩性指標對比Fig.12 Comparison of ride index in the middle of car body

安全性指標定剛度模型變剛度模型脫軌系數0.490.44輪重減載率0.430.39輪軌橫向力/kN27.527.3傾覆系數0.400.38

因此采用變剛度模型的平穩性性能有所降低，其安全性指標在曲線上比較關注的脫軌系數和輪動減載率都有所降低。

3 車輪磨耗仿真分析

車輪磨耗預測主要包括以下步驟：

步驟1車輛動力學仿真，通過SIMPACK建立車輛動力學模型，計算出每一積分步的輪軌接觸參數，并將輪軌接觸參數輸出。

步驟2局部輪軌接觸計算，采用Karlker算法重新劃分接觸斑網格，區分黏著區和滑動區，計算磨耗模型需要的參數。

步驟3車輪磨耗計算，計算接觸斑磨耗深度并線性插值累加到踏面上，并將累加后的磨耗深度進行平滑。

步驟4踏面更新。

其計算流程如圖13所示。

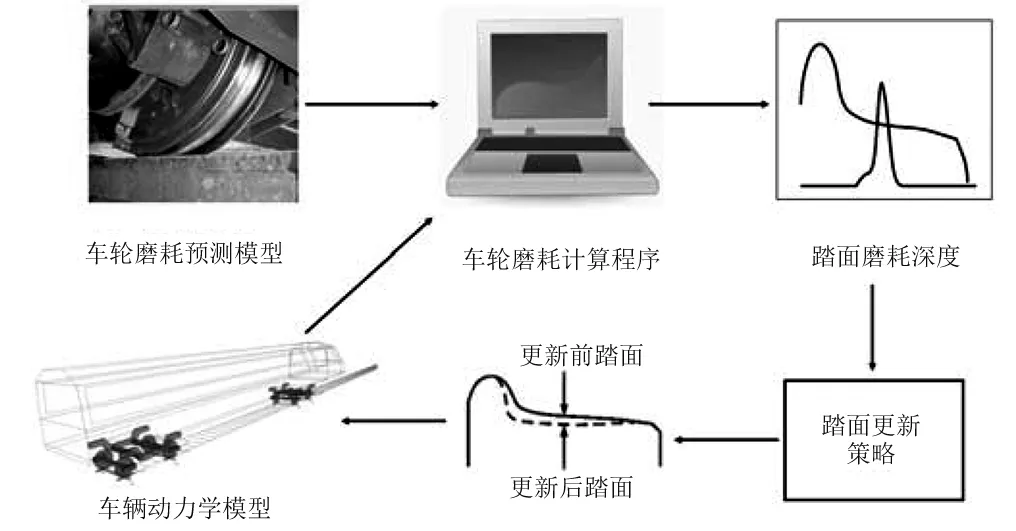
圖13 車輪踏面磨耗計算過程示意圖Fig.13 Diagram of wheel tread wear calculation process

3.1 直線工況下車輪磨耗

仿真踏面為LM踏面，軌面為60軌。軌底坡為1∶40。在600 m直線上兩種模型的車輪磨耗深度，采用實測線路軌道激擾。磨耗深度計算采用zobory模型，圖14給出了兩種模型在直線工況下的車輪磨耗深度值，當采用定剛度模型時車輪磨耗深度相對于定剛度模型明顯減小，1位輪對左輪磨耗深度減小55%,1位輪對右輪磨耗深度減小46%。因此在直線工況下變剛度模型能夠有效降低車輪磨耗。

3.2 曲線工況下車輪磨耗

仿真選用實測軌道譜，曲線半徑為500 m，緩和曲線長100 m，圓曲線長200 m，超高為120 mm，軌底坡為1∶40。采用Zobory模型計算了左右車輪磨耗深度。從圖15可知，當采用定剛度模型時，1位輪對左車輪磨耗深度為70×10-9m；當采用變剛度模型時，1位輪對右車輪磨耗深度為19×10-9m，且磨耗更均勻，車輪最大磨耗深度減小72.8%。當采用定剛度模型時，1位輪對右車輪磨耗深度為55×10-9m，采用變剛度模型時，1位輪對右車輪磨耗深度為18×10-9m，車輪最大磨耗深度減小67.3%。因此，從磨耗深度的仿真結果來看，變剛度模型有效地降低了地鐵車輛通過曲線時的車輪磨耗。

圖16給出了不同曲線半徑下，計算了基于定剛度模型和變剛度模型車輪磨耗深度。隨著曲線半徑的增大，定剛度模型和變剛度模型車輪磨耗深度都不斷降低，兩種模型的磨耗深度之差逐漸減小。可見，曲線半徑越小，變剛度模型的在減緩磨耗方面作用更加顯著。在300 m，500 m，800 m和1 000 m曲線半徑下，變剛度模型磨耗深度均小于定剛度模型磨耗深度。

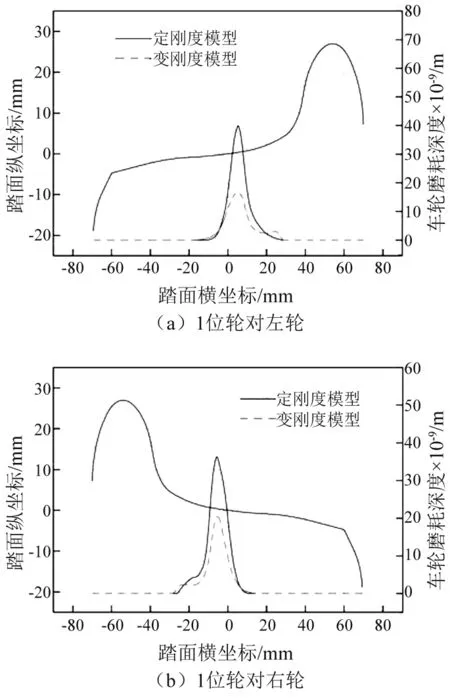
圖14 直線工況下車輪磨耗深度Fig.14 Wheel wear depth under a straight line

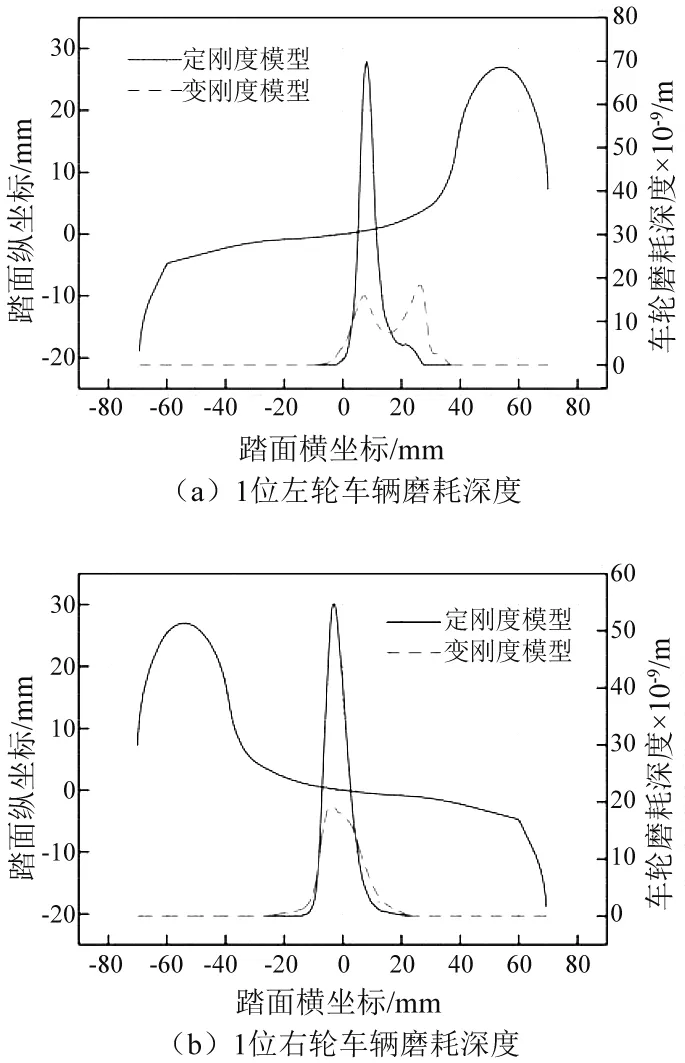
圖15 曲線工況下車輪磨耗深度Fig.15 Wheel wear depth under a curve line

圖16 不同曲線下的磨耗深度Fig.16 Wheel wear depth under diffrent curve lines

3.3 長距離車輪磨耗預測

由于缺乏買際線路貨料，因此本文選用表4所示的線路。為了減少計算量，本文做了以下假設：①線路上左曲線和右曲線對稱分布；②列車不掉頭往返運行；③每條曲線或直線的摩擦因數均為3；④計算中不考慮鋼軌型面的磨損。基于以上假設，車輛第1，第4輪對左右車輪的磨耗相同，第2，第3位輪對左右車輪的磨耗也相同，在計算時給出第1位輪對車輪的磨耗仿真結果。

表4 線路設置參數

采用以上線路工況，現分別就就兩種模型進行5萬km里程的磨耗預測，給出了車輪磨耗后型面和車輛磨耗深度，如圖17所示。

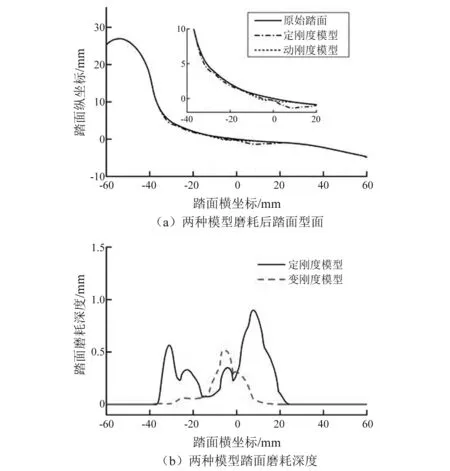
圖17 5萬km車輪磨耗預測Fig.17 Wheel wear prediction of 50 thousand km

由圖17可知，定剛度模型車輪的磨耗分布主要出現在車輪名義滾動圓士40 mm范圍內，變剛度模型車輪的磨耗分布主要出現在車輪名義滾動圓士20 mm范圍內。在運行里程為5萬km的情況下，采用定剛度模型的最大磨耗深度為0.9 mm，出現的位置在名義滾動圓外側10 mm處，同時在名義滾動圓內側30 mm處磨耗也較大，這是由于過曲線時輪緣根部頻繁接觸造成的，采用變剛度模型時最大磨耗深度均出現車輪名義滾動圓內側約5 mm處，最大磨耗深度為0.52 mm。最大磨耗深度減小42.2%。可以看出長距離運營工況下，采用變剛度模型可以有效減小車輪磨耗深度，改變車輪磨耗范圍。

地鐵車輛在實際線路中運行環境復雜，線路情況復雜，而仿真計算中僅采用了幾條典型的線路工況，仿真中輪軌材料的塑性流動、天氣因素對輪軌界面摩擦因數的影響均未在考慮范圍內。因此仿真計算結果與車輪實際磨耗可能存在一定的差異。但本文仿真作為理論分析，只作定性研究。

3.4 參數對車輪磨耗的影響

圖18中給出了串聯剛度、并聯剛度、并聯阻尼系數對車輪磨耗的影響，從18(a)可知，隨著串聯剛度的增大，車輪磨耗深度不斷增大，當從20 MN增大到40 MN時，車輪磨耗深度增大55%，從40 MN增大到60 MN時，車輪磨耗深度增大45.1%。從圖18(b)和圖18(c)可知，并聯剛度和串聯阻尼系數對車輪磨耗的影響較小，當并聯剛度從4 MN增大到8 MN時，車輪磨耗深度從31×10-9增大到了33×10-9，增大了6.41%，當串聯阻尼系數從0.2 MN增大到1 MN時，車輪磨耗深度增大2.4%。因此，串聯剛度對變剛度模型的車輪磨耗影響最大。并聯剛度和串聯剛度阻尼系數對對定剛度模型的車輪磨耗影響較小。

圖18 變剛度模型參數對車輪磨耗的影響Fig.18 Parameters influence of variable stiffness model on wheel wear

4 結 論

本文建立了變剛度節點模型，分析了其頻變特性和幅變特性。并分析了地鐵車輛變剛度轉臂定位節點的車輛動力學性能和磨耗性能。

(1) 變剛度模型提高了車輛直線運行時的臨界速度，改善了曲線通過性能，使得車輛通過曲線時接觸角和蠕滑力分別減小。

(2) 變剛度模型有效地改善了車輪磨耗，在直線工況，曲線工況下的變剛度模型車輪磨耗深度較定剛度模型有了大幅減小。隨著曲線半徑的增大，定剛度模型和變剛度模型車輪磨耗深度都不斷降低，兩種模型的磨耗深度之差逐漸減小。變剛度模型的在減緩磨耗方面作用更加顯著。

(3) 串聯剛度對車輪磨耗的影響最大，當串聯剛度從20 MN增大到60 MN時，車輪磨耗深度增大125%。并聯剛度和并聯阻尼系數對車輪磨耗影響較小，但參數選取時應結合動力學性能。