基于黏彈性理論的碰撞力計算方法及其在碰撞TMD中的應用

張井財， 李英娜， 薛啟超,2， 張春巍

(1. 哈爾濱工程大學 航天與建筑工程學院，哈爾濱 150001；2.青島理工大學 土木工程學院，山東 青島 266033)

地震作用下，相鄰結構或構件間的碰撞和沖擊常常會導致結構出現多種形式的破壞，如局部構件脫落甚至整體的坍塌。這種現象在世界上多次地震中都已經被觀察到[1-3]。結構或構件間的碰撞作用會導致構件破壞，但碰撞作用過程中的能量耗散作用也可以被利用，實現對結構的振動控制。碰撞式可調諧質量阻尼器(Pounding Tuned Mass Damper, PTMD)是在傳統的TMD系統上加裝黏彈性材料碰撞裝置，令附加質量與黏彈性碰撞裝置發生碰撞，輸入的能量在碰撞過程中不斷耗散，實現對主體結構振動的控制[4-11]。

無論是想避免(緩解)碰撞帶來的危害，還是想充分的利用碰撞耗能作用，準確地計算和分析碰撞過程中的相互作用是對碰撞問題進行研究的重要前提。

碰撞與沖擊是一個傳統的力學問題，經典的彈性理論忽略碰撞物體間的相互作用，以碰撞前后能量和沖量的變化來描述碰撞過程。針對碰撞物體間的相互作用，Goldsmith等[12]最先提出將單自由度碰撞過程中的接觸-回復過程的作用考慮為一個線性彈簧或非線性彈簧，并成功應用于碰撞分析。在此基礎上，針對碰撞過程中存在的能量耗散，加入了線性阻尼器的Kelvin模型被Anagnostopoulos[13]提出，能夠有效地考慮建筑結構間碰撞過程中的能量耗散。更為復雜的碰撞力模型大都基于Kelvin模型進行改進的結果，如Muthukumar等[14]推導了包含了非線性彈簧的Kelvin模型，即Hertz-Damp模型；Jankowski[15-16]在Kelvin模型和赫茲非線性彈簧理論的基礎上，將碰撞物體間的接觸過程分為逼近過程和分離過程，從而消除碰撞力曲線結束位置存在的拉伸作用，該模型是目前運用最廣的模型之一，如楊永強等[17-19]，對相鄰建筑(構件)的碰撞破壞問題的研究均采用此模型；趙大海等[20]則就隔震結構碰撞問題提出了改進Hertz-damp模型。

常用的碰撞力模型大都存在一些缺點，如模型參數缺乏具體的物理意義、適用性不強、小比例模型試驗結果在應用于真實結構時理論不完善等等。為了解決這些問題，本文結合接觸力學和線性黏彈性力學理論建立一種新的碰撞力模型分析方法，并根據兩個典型試驗和一個小型振動臺試驗驗證了該分析方法在單次碰撞和連續碰撞情況下的有效性。

1 黏彈性基本理論

1.1 黏彈性物質的本構關系

圖1是線性黏彈性固體的本構模型，圖1(a)是Kelvin模型，該模型通過并聯一個黏壺和一個彈簧來模擬物質的彈性和黏性性質，但是該模型無法模擬材料的瞬時彈性的性質。但對于一般材料，瞬時彈性是存在的，特別是在低速碰撞過程中材料的瞬時的彈性至關重要，于是有采用三參數模型如圖1(b)。

圖1 線性黏彈性物質的本構模型Fig.1 Linear viscoelastic constitutive models

對于三參數模型，分別定義σ,ε1,ε2,ε為模型總應力、Kelvin模型的應變、與之串聯的彈簧的應變和模型總應變，則有

ε=ε1+ε2

(1)

(2)

σ=E2ε2

(3)

式中：E1,E2和C1為三參數黏彈性模型的參數，見圖1(b)。寫成三參數模型的標準形式

(4)

其中，

(5)

由彈簧、阻尼通過串、并聯方式得到的更復雜的黏彈性本構關系如圖1(c)，本構關系可以統一寫成

(6)

為便于書寫，現引入微分算子

(7)

那么，以上本構關系可以統一寫成

Pσ=Qε

(8)

1.2 拉普拉斯變換域內黏彈性材料的本構方程

由前文，引入微分算子后，黏彈性物質的本構方程得到了形式上的簡化，但是本質上還是微分關系式，仍然不便使用。考慮到在拉普拉斯變換域內，黏彈性物質的應力應變可以轉換成線性關系，該關系在形式上和原物理空間下線彈性的本構關系相同，因此可以大大簡化使用過程。此時，在拉普拉斯變換域內解答一個黏彈性問題和在原物理空間下的線彈性問題是一致的(彈性-黏彈性對應原理)，在求得拉斯變換域內的解后再通過逆變換即可以得到原物理空間下的解。

黏彈性材料在拉氏變換下的本構關系為

(9)

(10)

寫成類似線彈性本構關系的形式

(11)

(12)

2 基于黏彈性理論的碰撞力模型

2.1 基本假設

(1)忽略碰撞區的慣性效應。土木工程領域的碰撞，應變范圍約在10-4～10-2，屬于傳統的低速碰撞問題，因此碰撞接觸區質量的慣性效應可以忽略。

(2)碰撞過程中的能量耗散只來源于材料的黏彈性性質。實際上，幾乎所有材料都具備黏彈性性質，也完全可以用黏彈性模型予以描述。傳統的材料如混凝土、鋼材均可視為是黏彈性材料，完全線彈性材料C=0。

2.2 分析過程

具體分析流程如圖2所示，首先需要對模型進行簡化，再借助接觸力學獲得其準靜態的力-位移表達式，最后通過軟件(MATLAB)進行拉氏變換和逆變換獲得碰撞力的時域表達式。

由接觸力學理論，兩物體發生碰撞后碰撞力按照式(13)計算

F=D(A,R,l)E*δα

(13)

式中：F為碰撞兩者間的碰撞力；D(A,R,l)和α為考慮了碰撞兩物體接觸面積、接觸面的曲率半徑等條件的參數；δ為碰撞侵入位移；E*為碰撞兩者的等效彈性模量。

將式(13)做拉普拉斯變換得到式(14)

(14)

再將式(14)進行一次拉普拉斯逆變換就得到了碰撞力時域的表達式(15)

(15)

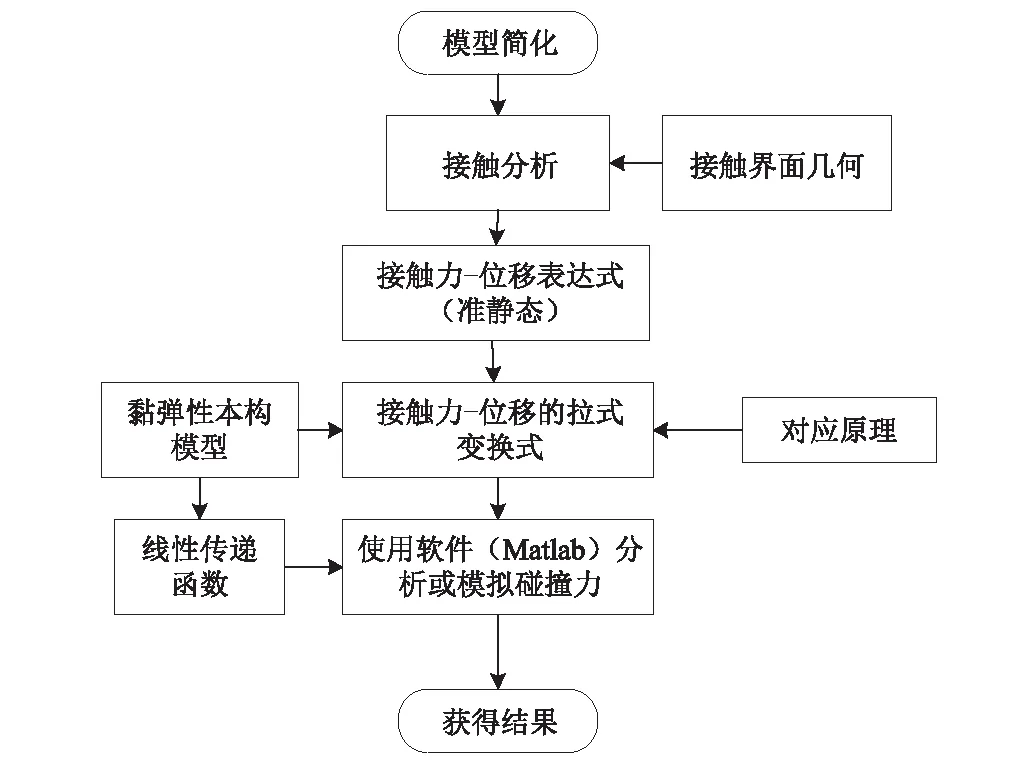
圖2 基于黏彈性理論的碰撞力分析方法分析流程Fig.2 Sketch of the proposed pounding force analysis model

3 基于黏彈性理論的碰撞力模型驗證

為研究兩物體之間的碰撞，不同的學者或提出或改進了諸多碰撞力模型，不同的模型有不同的計算思路和適用范圍。目前運用較多的有四種：線彈性模型(Linear Elastic, LE)、非線彈性模型(Non-Linear Elastic, N-LE)、線性黏彈性模型(Linear Viscoelastic, LVE)和非線性黏彈性模型(Non-Linear Viscoelastic, N-LVE)，如圖3所示。本文以這四種模型作為參照模型，對比驗證基于黏彈性理論的碰撞力模型的精度。

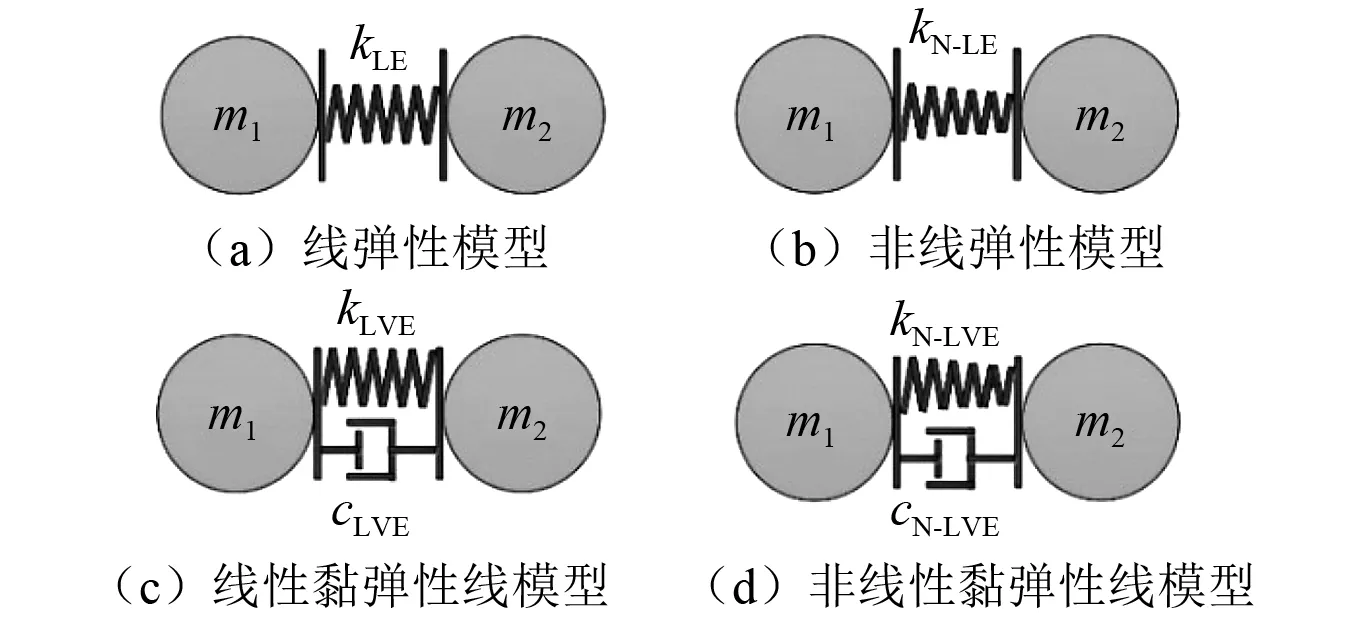
圖3 已有碰撞力模型Fig.3 Pounding force models

3.1 鋼-鋼碰撞

3.1.1 試驗概述

Goland等[21]于1959年完成該試驗，是一個鋼球從高處跌落與鋼平面之間的碰撞，示意圖如圖4所示。

圖4 鋼-鋼碰撞示意Fig.4 Model of steel-steel impact

運動方程寫成式(16)

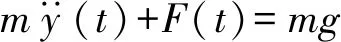
(16)

式中：m為小球質量；g為重力加速度；y為小球豎向位移，按照式(17)計算。

y(t)=δ(t)+h

(17)

式中：δ(t)為小球與鋼板的侵入位移；h為試驗跌落高度，本文h=5.08 cm。

由接觸力學，小球和鋼板間接觸力按式(18)計算[22]

(18)

式中：R為小球半徑，本文R=0.396 24 cm。根據黏彈性力學的對應原理，在拉氏變換域內有

(19)

再做逆變換得到

(20)

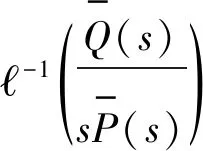
本文采用以碰撞力峰值相等的擬合方式來驗證提出的模型，采用MATLAB自編循環程序擬合目前已有碰撞模型的參數，具體的循環過程如圖5所示。

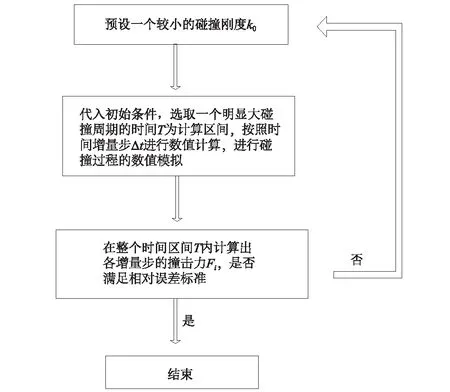
圖5 擬合流程Fig.5 Sketch of fitting analysis

相對誤差標準按式(21)計算

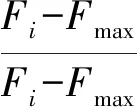
(21)

采用式(22)來計算各個模型的相對誤差。

(22)

(23)

式中:n為采樣點個數。

3.1.2 模擬結果

圖6(c)是鋼-鋼碰撞力時程曲線。線性黏彈性模型(LE)、非線性黏彈性模型(LVE)在碰撞初期均出現了碰撞力的跳躍現象，如圖6(a)所示。碰撞過程中，非線性黏彈性(N-LE)模型出現了力不連續現象如圖6(b)所示，在碰撞末期，線性黏彈性模型出現了拉力，如圖6(d)所示。這些均與實際碰撞過程不符。而本文模型(Proposed)沒有出現上述現象，說明本文模型是符合碰撞過程實際情況的。

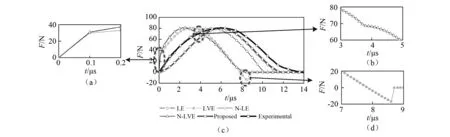
圖6 鋼-鋼碰撞力時程曲線Fig.6 Time histories of pounding force of steel-steel impact

表1給出了各模型的擬合結果。由表1可知，雖然上述擬合條件能夠讓已有碰撞力模型保證峰值力為80.7 N，但一方面在碰撞持續時間上，線性彈性模型(LE)、線性黏彈性模型(LVE)、非線彈性模型(N-LE)和非線性黏彈性模型(N-LVE)分別為10.0 μs，8.7 μs，11.2 μs和8.4 μs，而實際碰撞持續時間為13.8 μs，各模型的碰撞持續時間誤差分別是27.5%，37.0%，18.8%和39.1%，而本文模型峰值力86.0 N，持續時間11.2 μs，峰值力和持續時間相對誤差只有6.2%和18.8%。而模型的相對誤差Ψ為19.4%，也是所有模型中最小的。

同時，可以看出在本次試驗中，本文模型和非線彈性模型(N-LE)結果接近，而兩者的碰撞力-時間曲線也較接近，表明整個碰撞過程接近彈性碰撞。

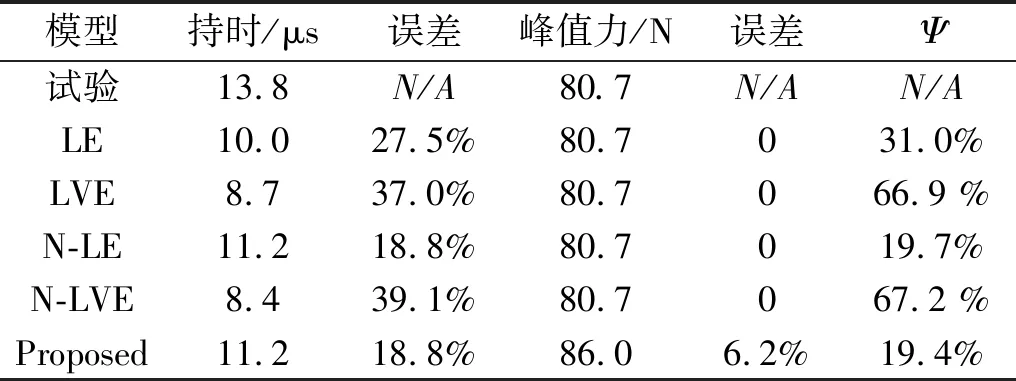
表1 鋼-鋼碰撞各模型擬合結果

圖7是各模型侵入位移和碰撞力之間的關系曲線。由圖，非線性黏彈性(N-LVE)和線性黏彈性(LVE)兩種模型曲線形成了滯回環，滯回環的面積即碰撞過程中的能量耗損，表明用這兩種模型描述的碰撞發生了塑性碰撞，碰撞過程能量耗損比較嚴重，與實際情況不符。其余三種模型幾乎是沿原路徑返回，表明該過程是近似彈性碰撞，能量耗損較小。

圖7 鋼-鋼碰撞力-侵入位移曲線Fig.7 Pounding force-indentation relationship of steel-steel impact

綜上，本文模型可以精確合理的模擬鋼-鋼碰撞的整個過程，無論是峰值力、碰撞時間還是碰撞力相對誤差都比現有的模型有明顯優勢。

3.2 混凝土-混凝土碰撞

3.2.1 試驗概述

Mier等[23]于1991年完成。如圖8所示，碰撞的兩者分別是尺寸為0.25 m×0.25 m×20 m的混凝土預應力梁和帶有圓形碰頭的混凝土擺錘。擺錘強度等級B30(美標)，強度38.2 N/mm2，質量570 kg，碰頭處為一半徑0.2 m的半球。與梁相撞時擺錘速度v1=0.5 m/s。

圖8 混凝土-混凝土碰撞試驗裝置圖Fig.8 Experimental setup concrete-concrete impact

模型簡化成圖9后，擺錘的運動方程為

(24)

式中：L為簡化后的單擺擺長，x是擺錘水平方向的位移。

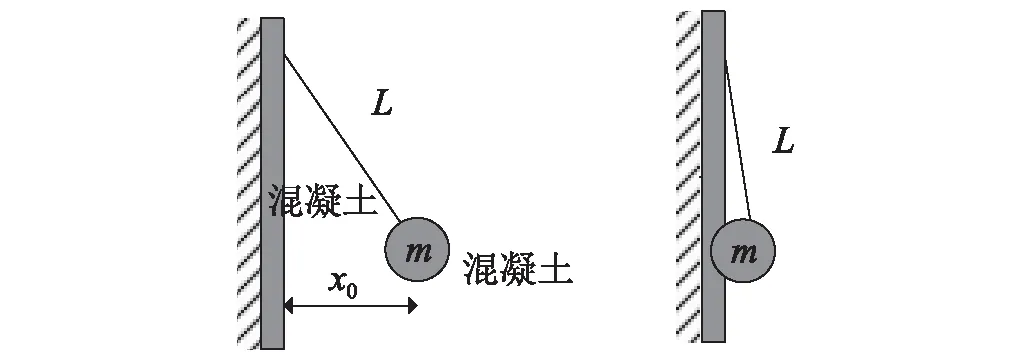
圖9 混凝土-混凝土碰撞計算模型Fig.9 Model of concrete-concrete impact

3.2.2 模擬結果

圖10(c)是混凝土-混凝土碰撞力時程曲線，在鋼-鋼碰撞中精度較高的非線彈性模型(N-LE)和線性彈性模型(LE)模擬結果和試驗結果偏差都非常大。從峰值力出現時間來看，前者在4.3 ms附近，后者在5 ms附近，而試驗峰值發生時間在2.1 ms附近。碰撞持時前者9 ms左右，后者10 ms左右，而試驗持時只有6 ms左右。這些都表明彈性模型已經無法描述混凝土-混凝土碰撞過程。

實際上，從Mier等的試驗結果來看，該過程中最大的碰撞力為100.8 kN，而按照相同接觸條件下的靜態加載形式，其徑向侵入位移為1.3 mm左右，那么碰撞力產生的壓強96.8 N/mm2左右。考慮到低速撞擊時，其侵入位移要更小，那么碰撞力肯定已經超過混凝土的強度(38.2 N/mm2)，換言之，混凝土擺錘碰頭處已經發生劣化，存在塑性變形(圖11是試驗原圖)。

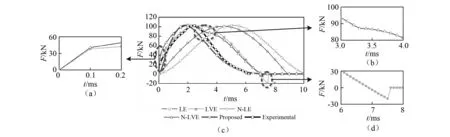
圖10 混凝土-混凝土碰撞力時程曲線Fig.10 Time histories of pounding force of concrete-concrete impact

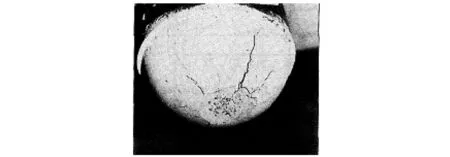
圖11 擺錘試驗后破壞情況Fig.11 Damage of striker specimen

如上所述，混凝土-混凝土碰撞是一個非彈性碰撞過程，雖然黏彈性模型取得了較好的模擬效果。但是，與鋼-鋼碰撞試驗類似，線性黏彈性模型(LVE)、非線性黏彈性模型(N-LVE)在碰撞初期均出現了碰撞力的跳躍現象如圖10(a)；碰撞過程中，非線性黏彈性模型(N-LVE)出現了力不連續現象如圖10(b)；碰撞末期，線性黏彈性模型(LVE)出現了拉力如圖10(d)，這些都是與實際不符的。而本文模型(Proposed)卻沒有出現上述現象，說明本文模型更符合碰撞過程實際情況。

圖12是碰撞力和侵入位移關系曲線，線性黏彈性模型(LVE)、非線性黏彈性模型(N-LVE)以及本文模型(Proposed)均出現了滯回環，這與混凝土-混凝土碰撞過程中出現了能量耗損是相一致的。但是，前文已經證明，該碰撞過程中存在劣化現象，發生了塑性變形，而這兩種黏彈性模型滯回環均沒有體現這一現象，說明這兩種模型僅僅是一種碰撞力上的純數值擬合，沒有考慮實際碰撞體的材料變化。相反，本文模型有明顯的殘余的變形，這說明本文模型與實際碰撞過程更加符合。

圖12 混凝土-混凝土碰撞力-侵入位移曲線Fig.12 Pounding force-indentation relationship of concrete-concrete impact

表2是各個模型的擬合結果。由表可知，在以峰值力為100.8 kN作為擬合邊界條件下，線性彈性模型(LE)、線性黏彈性模型(LVE)、非線彈性模型(N-LE)和非線性黏彈性模型(N-LVE)分別為8.8 ms,7.5 ms,10.2 ms和7.4 ms，與實際碰撞持續時間為6.1 ms相比，各模型的碰撞持續時間誤差分別是44.3%,23.0%,67.2%和21.3%，而本文模型峰值力100.2 kN，持續時間7.2 ms，峰值力和持續時間相對誤差只有0.8%和18.0%。在模型相對誤差上，本文提出的模型誤差只有12.5%，這遠小于已有的其他模型，表明本文模型有更高精度。

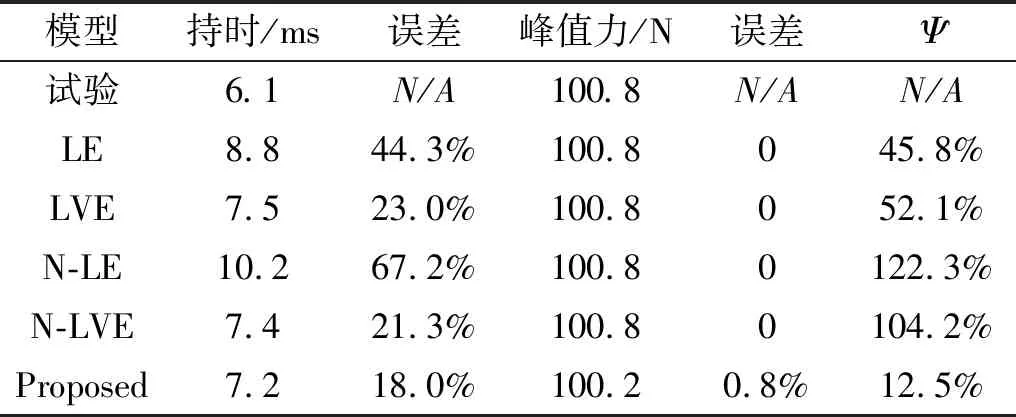
表2 混凝土-混凝土碰撞各模型擬合結果

綜上，對混凝土-混凝土這類非彈性碰撞，基于黏彈性理論的碰撞力模型依然能夠很好的符合實際碰撞過程，并有足夠高的精度。

4 PTMD的小型振動臺試驗

PTMD是一種新型的減振裝置，目前對其基本性能還缺乏足夠的認識，本文提出的碰撞力計算方法能否用于PTMD中也存在疑問。本節將自制小型PTMD裝置，并開展小型振動臺試驗。一方面驗證本文模型在連續碰撞過程中的有效性，另一方面驗證PTMD減振有效性，給出其基本動力學性能描述，拓展本文模型的應用范圍。

4.1 試驗概述

試驗在東北林業大學結構實驗室完成(見圖13)。主結構為一在頂端附有配重的鋼管。圓管內徑3 mm外徑5 mm。PTMD結構由L型梁、PTMD配重和粘有一層黏彈性聚氨酯黏彈性體的鐵環(兩者共同組成振動限制器)組成。主結構總重2.5 kg，PTMD配重50 g。整個裝置安裝于振動臺之上。振動臺與控制臺相連。實驗的振動限制器與主結構通過一根半徑2 mm的細鐵棒相連，鐵棒穿過主結構鋼管通過螺栓緊固。鐵環開有螺孔，與細鐵棒之間可拆卸，通過安裝不同半徑的鐵環即可獲得不同預留間隙的PTMD。當沒有鐵環時，PTMD預留間隙可以認為是無限大，即PTMD退化成為TMD。由于試驗條件所限，無法直接得到碰撞力曲線。本試驗采用對比結構響應的方法來間接驗證本文提出的碰撞力模型的精確性。

圖13 PTMD的小型振動臺試驗裝置Fig.13 Experimental setup of shake table test of PTMD

選取El地震波前10 s加速記錄激勵和初始位移為0.02 m的自由振動兩種工況進行試驗。同時為了驗證本文模型，結構被簡化成單自由度體系后在MATLAB/SIMILINK中進行模擬，解算方法采用四階的龍格庫塔法(OED4)，時間步長0.01 s，模擬時間10 s。

試驗所使用的振動臺為江蘇東菱振動儀器公司生產的型號ES-050-120 /LT0202的振動試驗機，采用兩個激光位移傳感器來監測主結構質量塊和配重質量塊的位移響應。

4.2 試驗結果

圖14和圖15分別是兩種工況的主結構位移時程曲線，由圖可得以下三點結論；

①PTMD能夠有效減輕結構在El激勵下的振動。PTMD可以使結構的最大位移從0.019 m下降到0.014 m(試驗結果)，減振率26.3%。在3～4 s和6～9 sPTMD的減振效果尤其明顯。

②PTMD可以使結構在自由振動過程中快速達到靜止狀態。如不附加PTMD，結構位移由0.02 m下降到0.005 m需歷時將近5 s，而PTMD可以將這個過程縮短至1.75 s左右(試驗結果)。這表明PTMD加速了結構的能量耗散。

③試驗結果(實線)和模擬結果(長虛線)雖然沒有完全重合，但是整體上符合較好。說明試驗結構和模擬結果是接近的。限于設備問題，無法采集碰撞力的實際情況，但是結構在振動過程中發生了碰撞，而碰撞對結構振動的影響直接的反應就是結構的振動響應，數值模擬和試驗結果符合較好，說明本文提出的碰撞力模型對連續碰撞工程也是適用的，并且有足夠的精度。

圖14 結構在El地震波作用下的位移時程曲線Fig.14 Displacement time history excited by El wave

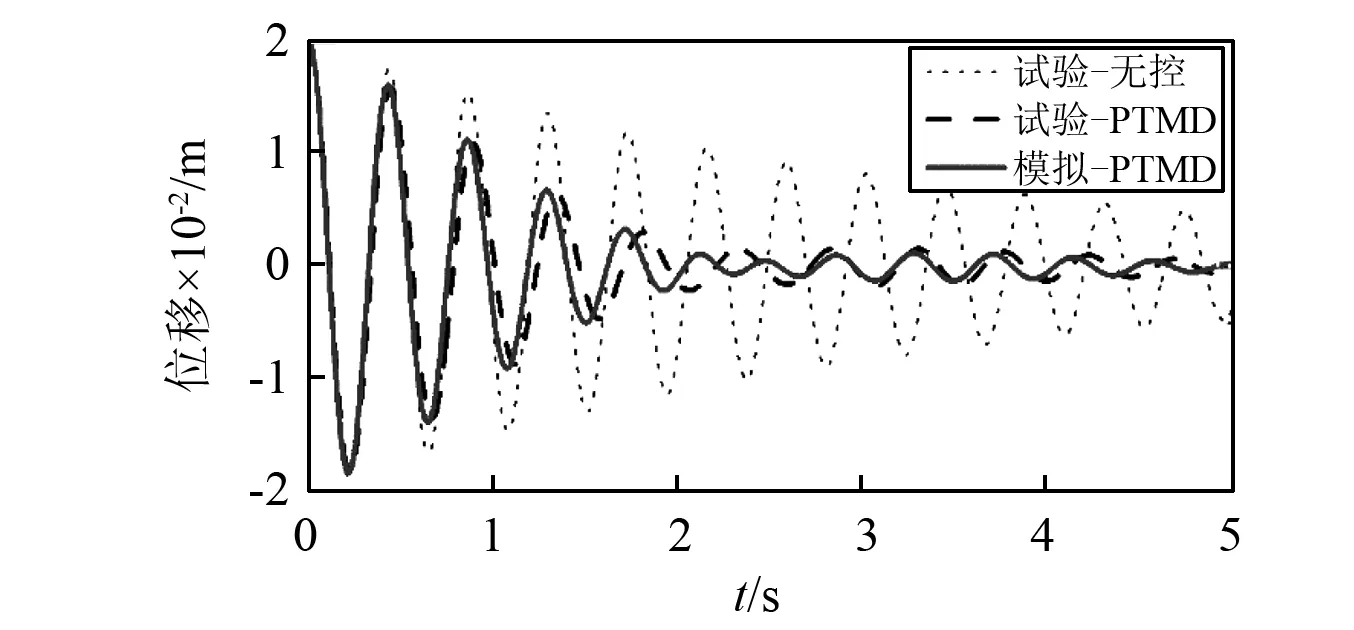
圖15 結構具有初始位移0.02 m的自由振動位移時程曲線Fig.15 Free vibration case with an initial displacement=0.02 m

5 結 論

本文提出了基于黏彈性理論的碰撞力分析理論，推導了該方法的計算公式，給出了計算流程。根據已公開發表的鋼-鋼碰撞和混凝土-混凝土碰撞試驗數據驗證了基于黏彈性理論的碰撞力模型，并開展了自制PTMD小型振動臺試驗，得到以下結論：

(1)基于黏彈性理論的碰撞力模型既能夠精確的描述彈性碰撞過程也能夠精確的描述非彈性碰撞過程。鋼-鋼的碰撞是一個近似彈性碰撞的過程，混凝土-混凝土的碰撞過程中發生了劣化和塑性變形，是一個非彈性碰撞過程，本文提出的模型在峰值力、碰撞時間和相對誤差方面的精度均高于現有模型。

(2)與現有模型相比，基于黏彈性理論的碰撞力模型可以獲得塑性碰撞過程的殘余變形，并且沒有出現線性黏彈性模型在碰撞初期發生碰撞力跳躍現象和在碰撞后期的拉力現象。也不會出現非線性黏彈性模型碰撞初期碰撞力跳躍和碰撞力過程中碰撞力不連續現象。這表明本文模型能夠更精確合理的描述碰撞過程。

(3)開展了自制PTMD小型振動臺實驗，實驗結果與數值模擬符合較好，說明本文模型可以較為精確的模擬鋼材與黏彈性材料之間的連續多次碰撞問題。

(4)PTMD可以有效抑制結構在外激勵下結構響應，也可以加快結構在自由振動下的能量耗散，使結構快速靜止。