艦用中低頻偽速度譜測量擺性能研究

趙鵬鐸， 曾澤璀,， 張 磊,， 閆 明

(1.海軍研究院，北京 100161；2.沈陽工業大學 機械工程學院，沈陽 110870)

現代艦船在海戰中必會面臨非接觸爆炸引起的沖擊破壞問題，主要的艦載機電設備和武器電子設備可能因承受過大的沖擊載荷而遭受破壞，導致艦船喪失戰斗力，處于不利局面[1]。

因此如何準確評估非接觸爆炸沖擊載荷對艦船設備破壞能力是一個十分重要課題。偽速度譜使用四參數對數坐標表示不同固有頻率系統在沖擊載荷作用下結構的最大相對位移、最大相對速度和最大加速度曲線變化趨勢，能夠簡單明了地反映沖擊載荷的破壞能力，用于確定沖擊環境，指導受沖擊系統的設計，廣泛應用在工程實踐中[2-3]。目前獲取偽速度譜的途徑主要有兩種：理論計算方法和傳感器測量方法。理論計算方法主要包括：有限元瞬態動力學計算方法和Duhamel積分方法。傳感器測量方法主要包括：機械式偽速度譜測量儀、振子式偽速度譜測量儀、電模擬式偽速度譜測量儀和數字分析方法。理論計算方法中，沖擊載荷曲線都是針對理想沖擊載荷曲線，從而獲得的偽速度譜也比較理想；而在傳感器測量方法中，由于傳感器自身特性產生的測量誤差導致沖擊信號測量不準，降低了偽速度譜的完整性和準確性。

目前，由于壓電加速度計具有體積小測量頻域寬等優點，廣泛應用于加速度測量領域。測量偽速度譜主要方法是利用壓電晶體加速度計測量沖擊載荷的時域曲線并進行數據處理獲得偽速度譜，但是，當沖擊載荷較大時會激起加速度計的諧振峰，使其產生的電荷不能快速釋放，從而產生零漂，零漂現象會影響中低頻偽速度譜測量的完整性和準確性[4-9]。所以需要利用簧片儀和低頻振子兩種測量裝置對加速度計測量得到的偽速度譜進行補充和相互驗證。但是，簧片儀和低頻振子都無法單獨測量獲得完整的中低頻偽速度譜曲線，而且簧片儀在測量低頻譜時，由于末端質量位移響應比較大，導致簧片儀根部應力過大而發生斷裂，所以低頻簧片儀能測頻率最低為5 Hz[10]；低頻振子在測量5 Hz一下的低頻譜時由于自身固有頻率低，具有彈簧的拉伸、壓縮量大和質量塊重的缺點，固有頻率為9.62 Hz的低頻振子僅質量塊重量就為8.4 kg[11]。

因此，需要研究體積小、重量輕的一種新型中低頻偽速度譜測量裝置來代替低頻振子和簧片儀，獨立完成中低頻偽速度譜的測量。沖擊環境主要包括垂向沖擊和橫向沖擊，在水下非接觸爆炸作用下，水面艦船主要承受垂向沖擊，潛艇主要承受橫向沖擊。橫向沖擊對艦載設備的破壞能力不遜于垂向沖擊，并且各國設備抗沖擊標準中都涉及到橫向沖擊譜標準值[12-13]。所以橫向沖擊偽速度譜的測量同樣十分重要。接下來主要針對非接觸爆炸所產生的橫向沖擊環境，利用德國BV043/85標準中的橫向沖擊位移譜值作為參考，從而進行偽速度譜測量擺的性能研究。

1 測量擺原理及運動方程解析求解

1.1 測量擺原理

由于低頻振子重量大不方便攜帶、中頻簧片儀雖然結構緊湊但是存在多階模態響應疊加影響測量精度，從而設計一種新型的中低頻偽速度譜測量裝置，即測量擺。測量擺原理如圖1所示，其結構與簧片儀相似，為懸臂梁-集中質量塊結構，其與簧片儀的區別在于將簧片儀固定端的完全約束固定連接改變為鉸鏈彈性連接，并選用扭簧為彈性元件，其包括以下幾個部件：鉸鏈、扭簧、擺桿和質量塊。測量擺的工作原理：基礎在沖擊載荷作用下，其沖擊響應主要表現為，質量塊和擺桿繞著鉸鏈以一定的頻率和振幅振動。

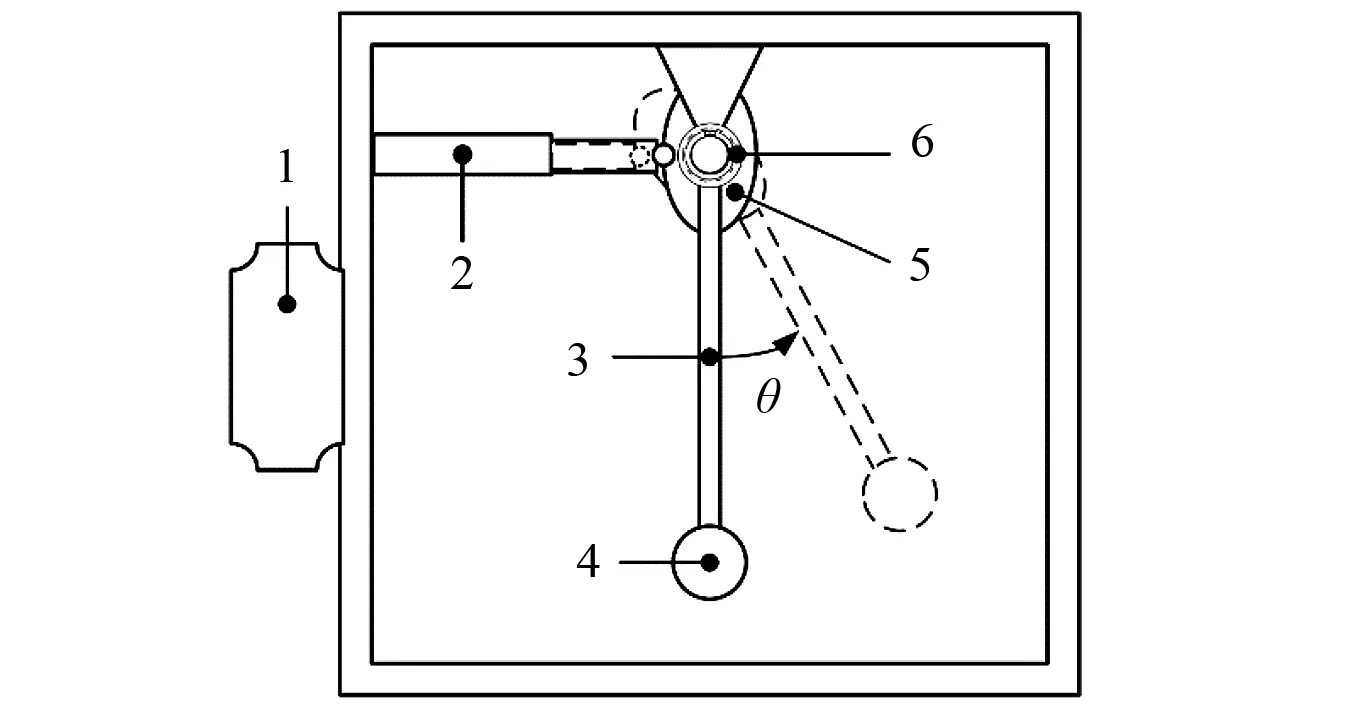
1-連接器；2-位移傳感器；3-擺桿；4-質量塊；5-凸輪；6-扭簧圖1 測量擺原理圖Fig.1 Schematic diagram of measuring pendulum

根據轉矩平衡定理式(1)，可以獲得沖擊測量擺運動微分方程式(2)

(1)

(2)

式中：kt為彈簧扭轉剛度，N·mm/rad；L為擺桿旋轉中心到質量塊重心的距離，mm；m1為質量塊量,kg；m2為擺桿質量,kg；θ為擺桿的擺角,rad。

由于sinθ的存在，式(2)為非線性方程。而且只有在θ<1°(也就是小振幅條件)，此時式(2)才能近似于線性方程。但是各國都有對應的沖擊環境標準，其中德國BV043/85標準中的橫向沖擊位移譜值為47 mm。因此測量擺的實際測量角度響應幅值高達30°，測量擺在沖擊譜測量過程中存在非線性效應。為研究測量擺在±30°范圍內的測量性能是否明顯受到非線性效應影響，分別利用解析法求解非線性方程、有限元方法和實驗進行研究，從而驗證測量擺用于實際偽速度譜測量的可靠性。

1.2 非線性方程解析求解

在這里引入sinθ的泰勒級數展開式來幫助求解方程，如式(3)所示。

(3)

所設計的測量擺在對應實驗沖擊載荷作用下其擺角不超過30°，其所對應的sinθ泰勒級數展開式前兩項與sinθ數值相差百分比在0.01%之內。因此sinθ泰勒級數展開式的前兩項就可以作為sinθ的近似解。通過聯立式(2)和式(3)可以獲得沖擊測量擺的運動微分方程為

(4)

根據Ritz-Galerkin方法，通過滿足控制非線性微分方程得到問題的近似解。現將非線性微分方程式(4)表達成

(5)

令

則式(5)可以表達成

(6)

假設式(6)的近似解為

(7)

式中:φ1(t)，φ2(t)，…，φn(t)為假定的時間函數；a1，a2，…，an為待定的權系數，如果把式(7)代入式(6)可得到近似函數方程為

(8)

并且通過求解積分方程式(9)獲得非線性微分方程的近似解

(9)

現以式(7)的一階近似解為例，求解非線性微分式(2)～式(5)，具體求解步驟如下：

令

(10)

將式(10)代入式(8)可求得

(11)

根據Ritz-Galerkin方法求解方程解

(12)

求解式(12)，得

(13)

因為式中A0不等于零，所以將式(13)轉化為

(14)

求解方程得

代入測量擺結構參數和初始條件，求解式(15)就可以獲得測量擺的固有頻率，其中A0值取決于瞬態動力學分析所獲得的最大角度響應。在這里分別計算5 Hz，10 Hz和20 Hz的測量擺，在計算中發現式(15a)的第一項解更接近與真實解，所以這里只列出式(15a)的解，其計算結果如表1所示。

2 有限元模態分析

為了計算沖擊測量擺仿真模態頻率，使用有限元軟件ANSYS的Mechanical/LS-DYNA模塊進行計算。創建沖擊擺有限元模型，其中使用BEAM188單元創建擺桿模型，材料為45鋼；使用COMBIN14單元創建測量擺的扭簧模型；使用MASS21單元創建測量擺的自由端質量塊模型。

根據測量擺實物尺寸創建幾何模型并劃分網格，并設定邊界條件進行模態分析，具體計算結果如表1所示，表中fl為Ritz-Galerkin方法計算頻率，fy為有限元模態計算頻率，fs為實驗模態頻率。從Ritz-Galerkin方法計算結果可以看出當沖擊角度響應較小時(小于30°)，使用一階近似解就可以獲得與數值解法相近的方程解。

表1 沖擊測量擺模態計算

由于所計算三種頻率的前三階模態振型類似，這里只列出20 Hz測量擺的前三階振型，如圖2所示。

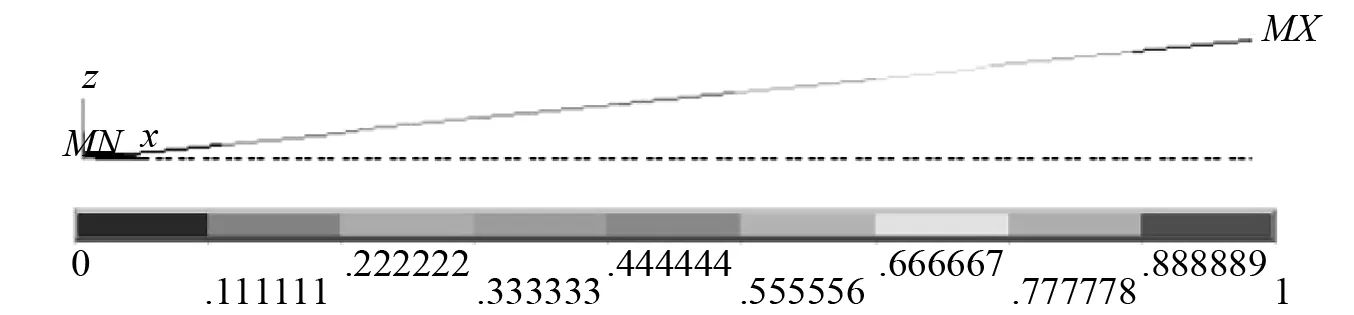
(a)一階振型

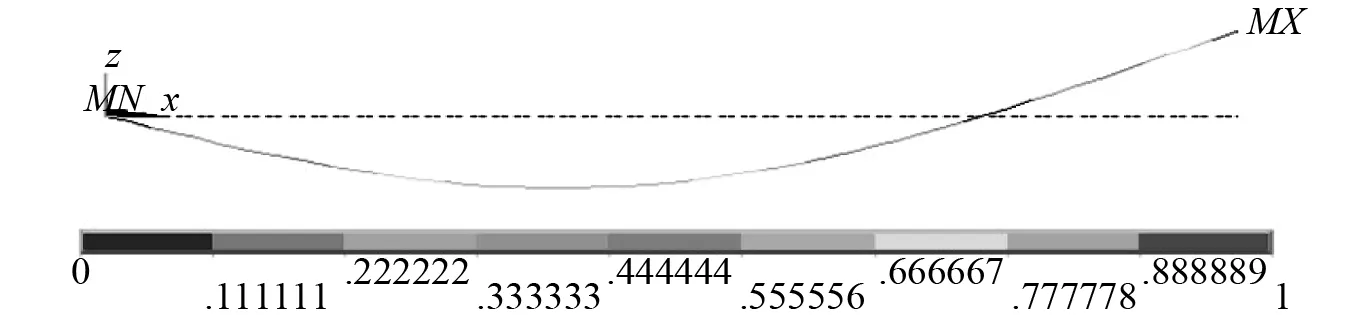
(b)二階振型

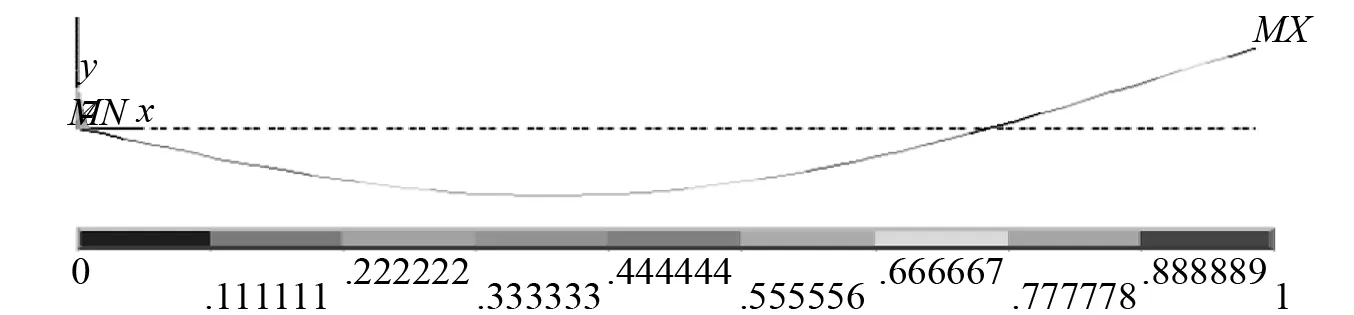
(c)三階振型圖2 測量擺前三階模態振型圖Fig.2 The first three modal shape of measuring pendulum

3 沖擊響應計算

在現代海戰中艦船經常受到水下非接觸爆炸沖擊，其主要表現形式為正負雙正弦波加速度時域曲線，即正負雙波曲線[14-15]。正負雙波曲線可以由兩個符號相反，時間延遲為脈沖寬度的正弦沖擊信號組合而成，正負雙波曲線函數為式(16)。

(16)

式中：l(t)為單位階躍函數。根據實際沖擊載荷波形幅值和脈寬換算出一條等效沖擊波形用于理論計算所用的理論載荷，如圖3所示。

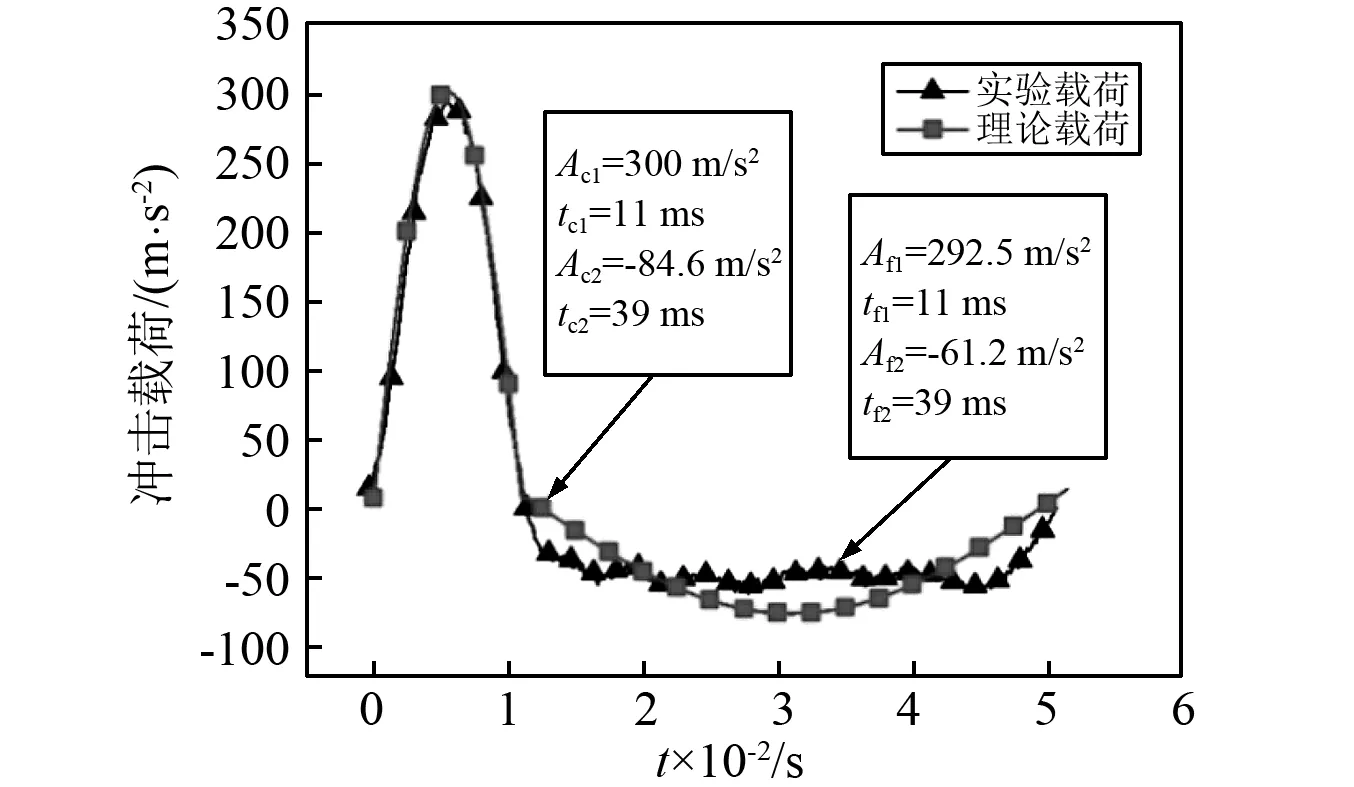
圖3 沖擊載荷時域曲線Fig.3 Real-time curve of shock loading

利用杜哈美積分方法求解系統在正負雙波曲線沖擊下的角度響應方程式(17)。

(17)

式中：wd為阻尼固有頻率；wn為系統固有頻率。將已知的正負雙波沖擊信號代入式(17)中就能求得系統最大角度響應。

使用MATLAB編寫程序計算固有頻率為5 Hz，10 Hz和20 Hz沖擊測量擺在無阻尼狀態下的沖擊角度響應，見表2，表中θl為杜哈美積分方法求解角度響應，θy為有限元瞬態響應方法求解角度響應。

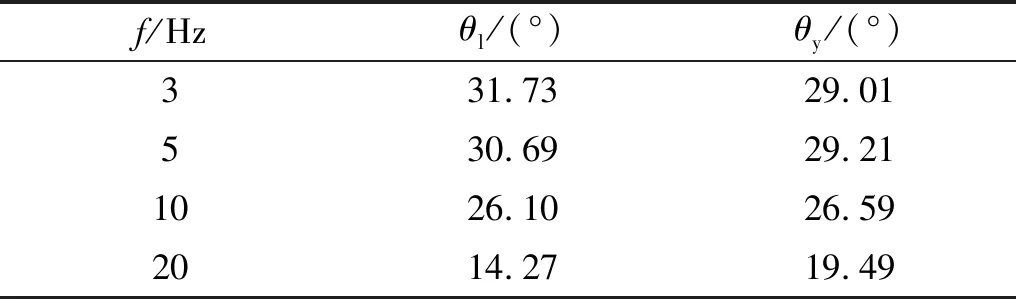
表2 測量擺沖擊角度響應

使用ANSYS有限元軟件，創建沖擊測量擺模型，并計算沖擊角度響應。由于實際實驗環境較為復雜，對于系統的阻尼系數難以得到精確測量，在本節中所采取計算阻尼系數的方法是通過初步確定系統阻尼比，從而獲得阻尼系數，再根據具體阻尼系數計算測量擺的理論沖擊響應。根據具體沖擊測量擺原理樣機的結構參數計算不同固有頻率所對應的臨界阻尼，如表3所示。

表3 測量擺臨界阻尼系數ct

在考慮阻尼比(ζ=0，ζ=0.05和ζ=0.15)的情況下計算沖擊測量擺的角度響應，其對應的沖擊響應曲線如圖4所示，并將最大角度響應轉換為水平分量的位移響應見表4。

圖4 測量擺角度響應Fig.4 Shock angle response of measuring pendulum

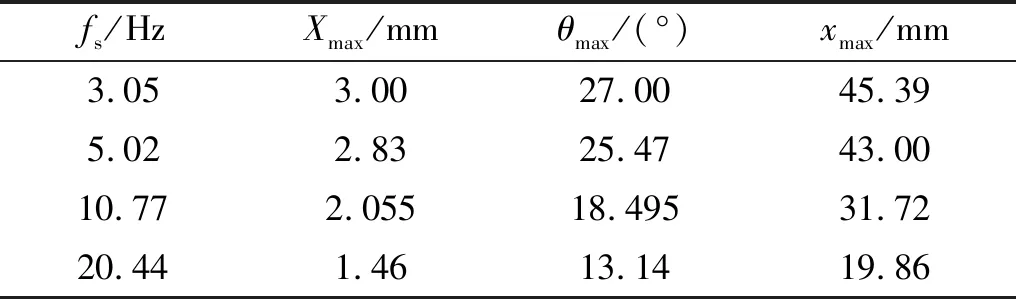
fs/HzXmax/mmθmax/(°)xmax/mm3.053.0027.0045.395.022.8325.4743.0010.772.05518.49531.7220.441.4613.1419.86

根據測量擺擺桿長度為100 mm，通過對擺桿的角度響應進行轉換可獲得質量塊在水平方向位移響應分量，并根據測量擺最大位移響應與偽速度的關系式(18)進行換算繪制中低頻段的偽速度譜，如圖5所示。

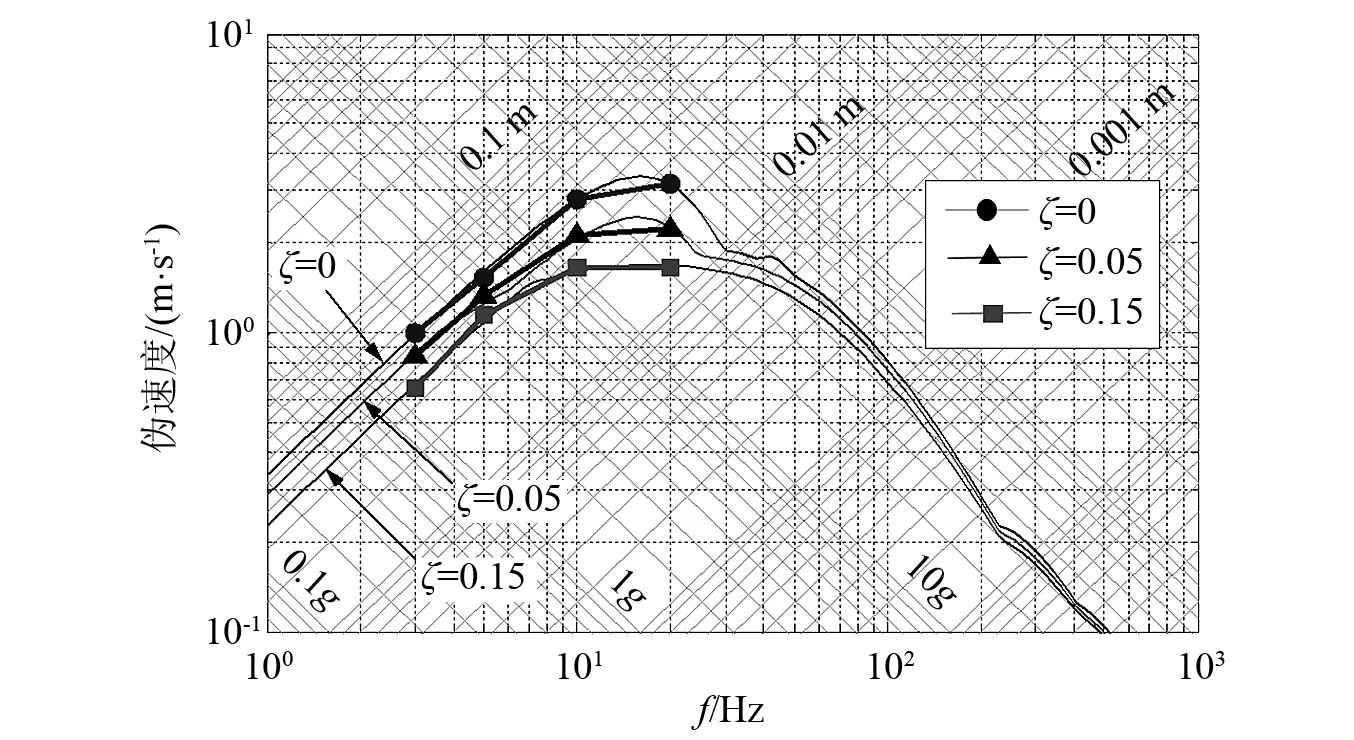
圖5 測量擺理論偽速度譜Fig.5 Schematic diagram of measuring pendulum

(18)

4 沖擊測量擺原理樣機實驗

4.1 掃頻實驗

為了測量沖擊測量擺原理樣機的實際固有頻率，使用振動實驗機進行掃頻實驗。本次實驗所使用振動實驗臺為蘇州蘇試試驗儀器有限公司生產的電動振動實驗系統，型號為：DC-3200-36；所使用的實驗樣品為3 Hz，5 Hz，10 Hz和20 Hz的沖擊測量擺；所使用的傳感器為INV9822型加速度傳感器。加速度傳感器一共兩個，分別為加速度計1和加速度計2。加速度計1，用于采集質量塊的響應信號即沖擊響應信號；加速度計2，用于采集實驗沖擊平臺的輸入信號即基礎輸入信號，測量擺實驗原理如圖6所示。

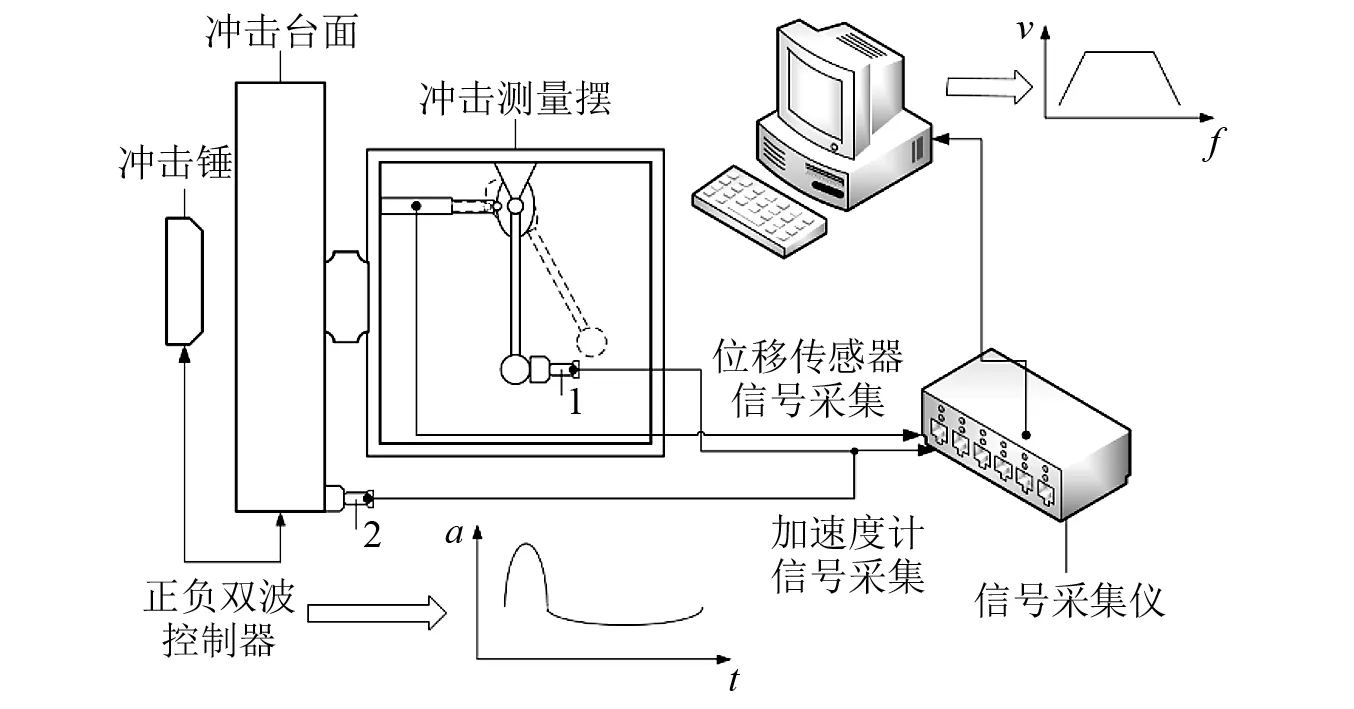
圖6 測量擺實驗原理圖Fig.6 The testing schematic of measuring pendulum

測量擺在實驗中的安裝方法，如圖7所示，其對應模態頻率為3 Hz。圖8中所示的測量擺為模態頻率為10 Hz，其質量塊為0.05 kg，擺桿質量為0.033 kg，扭簧剛度為51.2 N·mm/(°)，整體裝置質量約為4.1 kg，僅為對應固有頻率低頻振子質量塊質量的50%，體積長寬高為150×150×150 (mm)，可以看出測量擺明顯減小傳統測量裝置的體積和重量。

圖7 沖擊測量擺掃頻實驗(3 Hz) Fig.7 Frequency sweep test of measuring pendulum(3 Hz)

圖8 測量擺掃頻實驗(10 Hz) Fig.8 Frequency sweep test of measuring pendulum(10 Hz)

掃頻實驗原理，設定振動臺的掃頻范圍，通過觀察輸出信號與輸入信號之間的傳遞函數，觀察曲線的走勢，曲線峰值所對應的頻率點即為實驗原理樣機的掃頻共振點，通過測量共振點的頻率獲得實驗原理樣機的實際固有頻率，橫向掃頻實驗果數據如圖9所示。

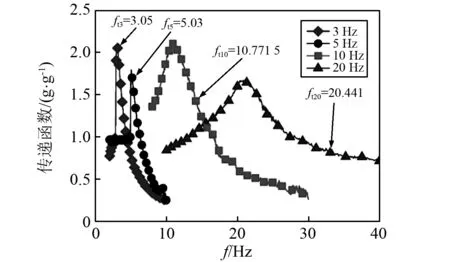
圖9 測量擺掃頻曲線Fig.9 Schematic diagram of measuring pendulum

從掃頻實驗結果可以看出，沖擊測量擺原理樣機固有頻率與實際理論設計固有頻率之間有一定的差別。

4.2 沖擊實驗

(1)沖擊載荷

為了測試沖擊測量擺測量偽速度譜的性能，使用電動振動實驗臺進行沖擊實驗，所設定的沖擊載荷為正波峰值30g，脈寬為11 ms；負波峰值-8.4g，脈寬為39 ms。實際通過加速度計測量實驗臺實際運動獲得如圖10所示的沖擊輸入載荷波形。

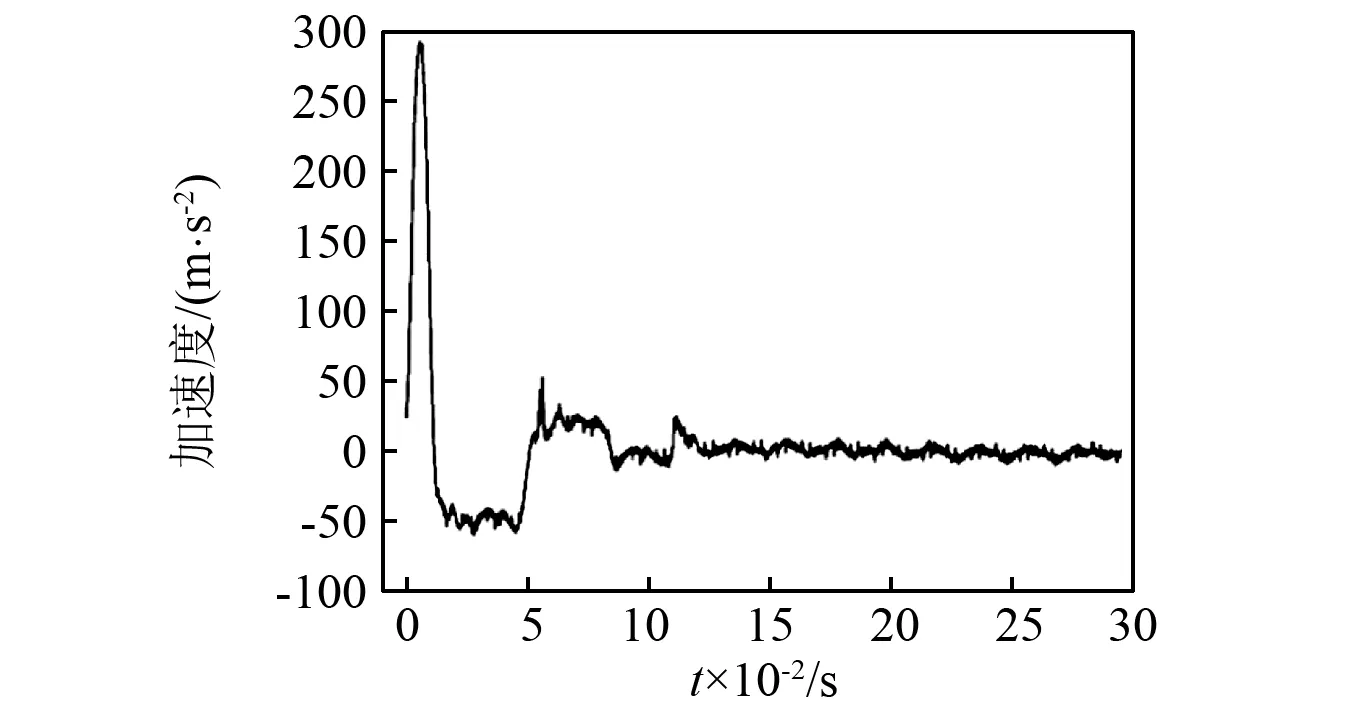
圖10 實驗沖擊載荷Fig.10 Testing shock loading curve

(2)沖擊實驗原理

為了更好地測量沖擊測量擺的沖擊響應，使用位移傳感器測量沖擊響應。測量沖擊測量擺的沖擊響應原理：使用位移傳感器測量凸輪升程間接獲得擺桿的擺角，具體工作原理如圖6所示。

根據上述的沖擊載荷對沖擊測量擺原理樣機進行沖擊實驗，通過對沖擊加速度輸入信號和加速度輸出信號進行濾波處理，并且將輸入和輸出加速度信號進行二次積分處理成時域位移曲線；通過位移傳感器輸出曲線計算沖擊測量擺的角度響應。

4.3 沖擊測量擺實驗數據分析

根據沖擊測量擺的測量原理，在規定的沖擊載荷作用下，位移傳感器測量響應曲線如圖11所示。圖中Xnmin為位移傳感器的初始位置(mm)，不同裝置上的位移傳感器由于裝配差別其對應的初始位置不同；Xnmax為位移傳感器的最大響應值(mm)。

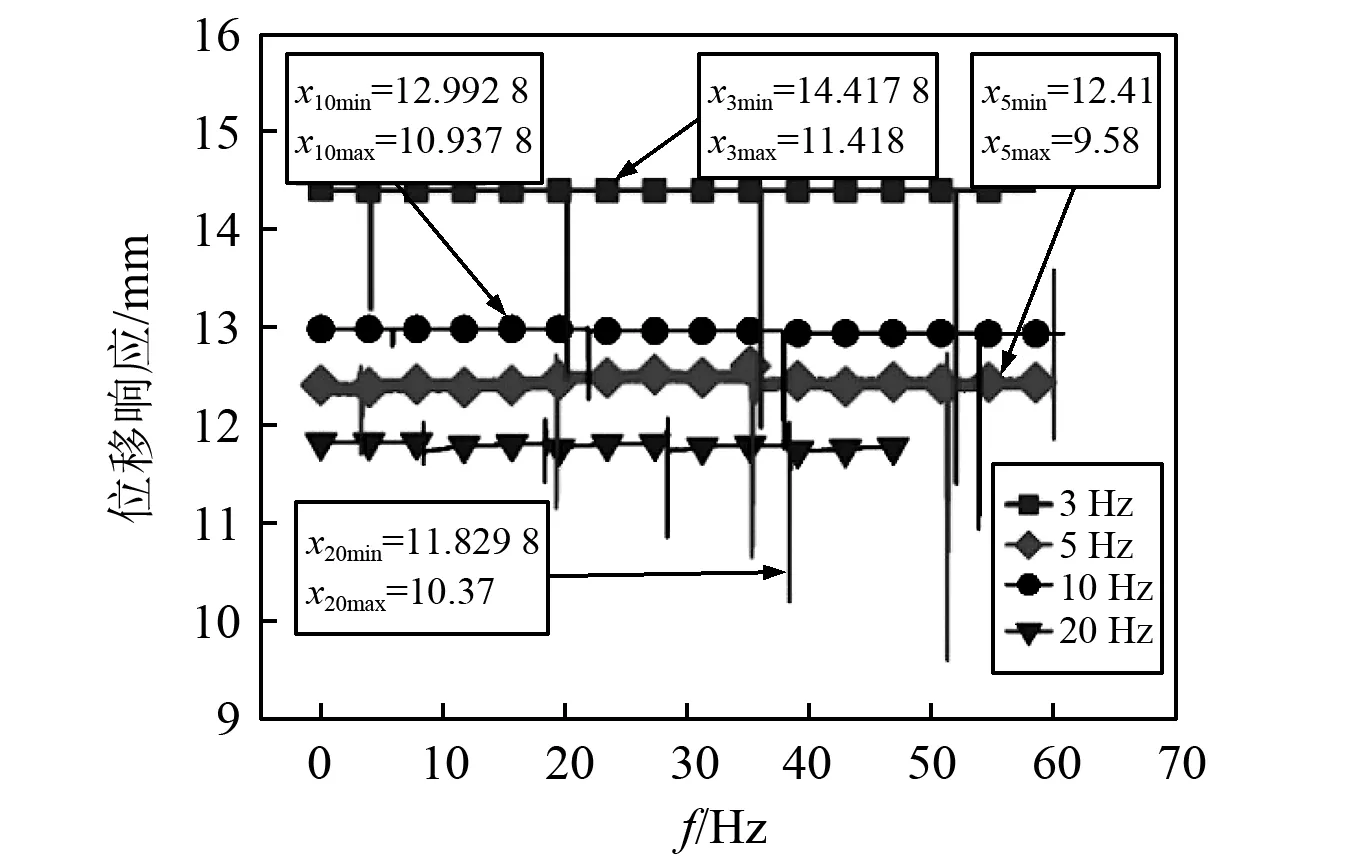
圖11 測量擺位移響應Fig.11 Shock displacement response of measuring pendulum

根測量擺凸輪機構與位移傳感器測量角度響應的原理，可以將實驗中所測量的位移傳感器最大位移響應轉換為測量擺的沖擊角度響應，其具體轉換公式如式(19)，測量擺水平位移響應如表4所示，表中fs為實驗固有頻率，Xi為初始位移，Xmax為最大位移，θmax最大角度響應，xmax最大水平位移響應，其中Xmax=Xnmin-Xnmax。

(19)

將測量擺與低頻振子所測得沖擊響應進行一定轉換后繪制成偽速度譜，如圖12所示。

5 結 論

通過建立測量擺運動微分方程獲得其模型的一階固有頻率，根據任意激勵下系統沖擊響應所涉及的杜哈美積分方法求解系統在正負雙波曲線沖擊下的角度響應；同時對測量擺模型使用ANSYS軟件進行模態計算和瞬態動力學分析獲得其對應的模態頻率和角度沖擊響應；最后對測量擺原理樣機進行掃頻和沖擊試驗，測量其固有頻率和角度沖擊響應。根據角度沖擊響應進行數據處理轉換轉變成偽速度譜，根據研究內容，主要結論如下：

(1)由于傳統加速度計在強沖擊作用下產生零漂現象導致中低頻段偽速度譜測量數值誤差為1～2個數量級，通過理論計算數據和實驗數據可以表明測量擺可以較準確測量中低頻段偽速度譜，并且通過沖擊實驗驗證了測量擺測量性能，可以準確校驗加速度計所測中低頻段的偽速度譜。

(2)測量擺相對傳統的低頻振子，減少了空間尺寸大小和裝置整體質量，模態頻率為10 Hz時其整體裝置質量僅為對應模態頻率低頻振子質量塊質量的50%；與簧片儀相比，測量頻域范圍廣，能夠測量5 Hz以下的偽速度譜。