一類5階KdV方程的孤立波解

周蘭鎖,尹曉軍

(內(nèi)蒙古農(nóng)業(yè)大學(xué)理學(xué)院,內(nèi)蒙古 呼和浩特010018)

1.引言

自從1834年,Russell首次觀察到孤立波以來,孤立子作為非線性科學(xué)的重要組成部分已經(jīng)滲透到了許多研究領(lǐng)域,主要分布在應(yīng)用數(shù)學(xué)、物理學(xué)、力學(xué)、大氣和海洋科學(xué)等交叉學(xué)科領(lǐng)域里[1?3].

近年來,非線性方程發(fā)展作為孤立子理論的載體一直是數(shù)學(xué)物理工作者研究的熱點(diǎn),主要尋求非線性方程的孤立子解以及解的適定性問題.目前對(duì)于非線性方程的求解方法已經(jīng)有很多,如:Jacobi橢圓函數(shù)展開法[4],同倫攝動(dòng)法[5],齊次平衡法[6],B¨acklund變換法[7],Hirota雙線性方法[8],Darboux 變換法[9],Sine-Cosine展開法[10?11]等.這些方法是求解非線性方程精確解的重要方法.但是,由于非線性方程的復(fù)雜性,至今沒有統(tǒng)一的求解方法.1895 年,Korteweg和他的學(xué)生de Vries研究淺水波運(yùn)動(dòng),推導(dǎo)出KdV方程并求得了精確解以來,KdV方程就被視為非線性數(shù)學(xué)物理的基本模型之一.后來,人們陸續(xù)在各個(gè)不同學(xué)科的實(shí)際背景下提出許多非線性偏微分方程,如mKdV,ZK,Schrdinger以及ZK-mZK方程等[12?15].

本文主要尋找一類5階KdV方程

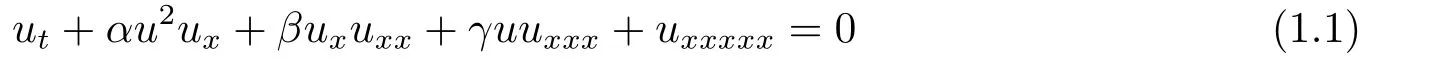
的孤立波解,這里α,β,γ是任意非零常數(shù),其中uxxx,uxxxxx表示色散項(xiàng).當(dāng)方程系數(shù)為(α,β,γ) = (30,20,10),(120,40,20),(270,60,30) 時(shí),稱為Lax方程[16?17],它廣泛應(yīng)用于量子力學(xué)、流體力學(xué)以及等離子體物理領(lǐng)域中.對(duì)于5階KdV方程,文[18]采用Jacobi橢圓函數(shù)展開法,獲得了5階KdV方程的一些精確解.文[19]利用Hirota雙線性方法研究了(2+1)維廣義5階KdV方程的單孤立子解以及雙孤立子解.文[20]根據(jù)Jost解的相容性原理,給出了求解高階KdV方程孤立子解的一種簡單方法.這里我們主要應(yīng)用Sine-Cosine展開法……