雙參數彈性地基上對邊滑支正交各向異性矩形薄板彎曲問題的辛本征函數展開定理

高立梅,額布日力吐,阿拉坦倉

(1.內蒙古大學數學科學學院,內蒙古 呼和浩特010021;2.呼和浩特民族學院,內蒙古 呼和浩特010051)

1.引言

由于彈性地基矩形板在機械和航天事業中有著十分廣泛的用途,所以國內外學者一直在研究彈性地基矩形板問題.經過學者們的不斷努力得到了一些解析解方法,如復變函數法[1]、有限積分法[2]、級數法[3?4]等.但是這些方法都具有一定的局限性,需要事先人為設定好試驗函數.為了改變這種局限性,鐘萬勰院士提出了辛彈性力學方法[5?6],使得許多力學中的實際問題得到解決[7?8].但是辛彈性力學方法也有一定的不足之處,例如,當對應Hamilton 算子的本征值和本征函數沒有具體解析表達式時,該方法并不能給出原問題的解析解.為此李銳提出了辛疊加方法[9],該方法使得各向同性板問題的多個邊值問題得到解決[10?12].但因為雙參數彈性地基上正交各向異性矩形薄板的彎曲問題比較復雜,所以尚未見到利用辛疊加方法處理該類問題的報道.到目前為止,關于雙參數彈性地基上正交各向異性矩形薄板問題辛彈性力學方法只研究了對邊簡支邊界條件的情形[13].由于雙參數彈性地基上正交各向異性矩形薄板的四邊固支和四邊自由邊界條件問題所對應Hamilton 算子的本征值和本征函數均給不出具體解析表達式,所以辛彈性力學方法給不出這兩類邊界條件問題的解析解,但我們可參照各向同性板的結論[12,14],應用辛疊加方法來展開這類問題的研究.基于上述情況本文研究了雙參數彈性地基上的正交各向異性矩形薄板對邊滑支條件下的彎曲問題.首先計算出相應Hamilton 算子的本征值及相應本征函數系.再證明出該本征函數系的辛正交性以及在Cauchy 主值意義下的完備性,之后利用辛本征函數展開法求出雙參數彈性地基上正交各向異性矩形薄板對邊滑支問題的一般解.最后將所得結論與已有文獻作對比驗證了所得解的正確性.本文所得結論為基于對邊滑支問題的辛疊加方法應用到正交各向異性矩形薄板的各類邊值問題中提供了理論基礎.

2.Hamilton 正則方程

雙參數彈性地基上的正交各向異性矩形薄板彎曲方程為

方程(2.1)的Hamilton 正則方程為

通過計算可驗證算子矩陣H滿足H?=JHJ,即H是Hamilton 算子矩陣,從而式(2.2)為薄板的Hamilton 正則方程.

3.本征值和本征函數系

為求解Hamilton 正則方程式(2.2),我們先求對應的齊次方程

由分離變量法求解式(3.1).令

將式(3.2)代入式(3.1)得到

式中μ為本征值,X(x)為相應的本征函數,記X(x) = (X1(x),X2(x),X3(x),X4(x))T,將式(3.3)展開得到

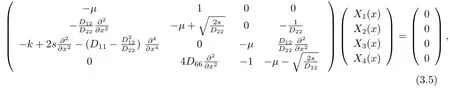
整理后得到

令X1(x)=eλx代入式(3.6)有

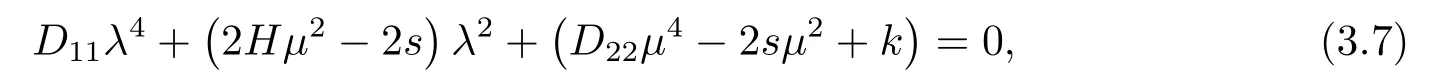
則

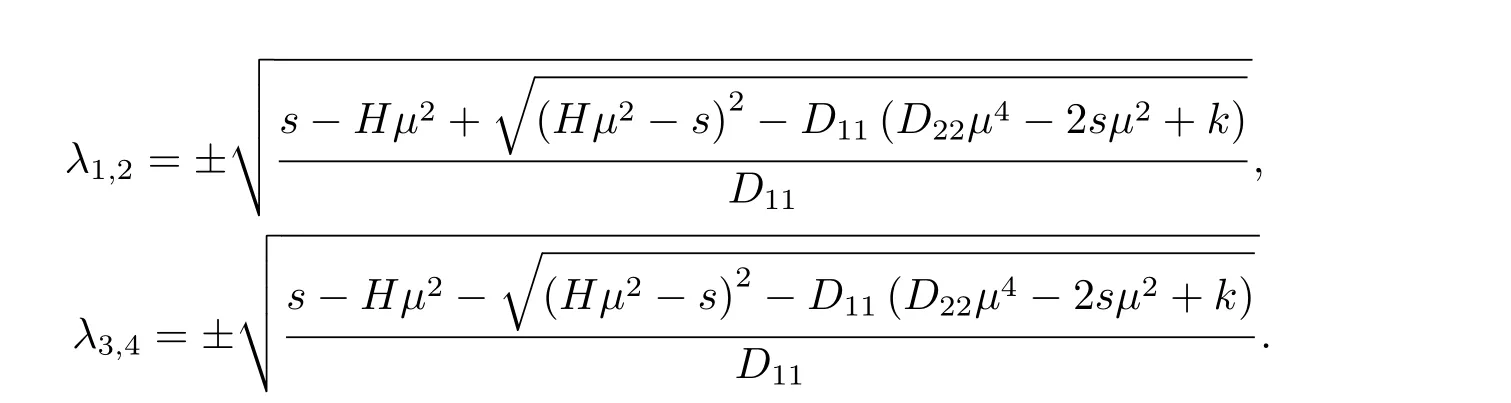
在式(3.6)中代入對邊滑支條件

計算其系數行列式,得

進而得到

設式(3.6)通解為

將式(3.9)和式(3.10)代入式(3.8)得到

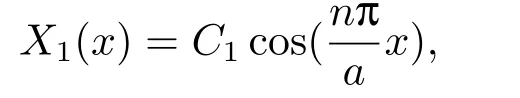
其中C1為常數.

將式(3.9)代入式(3.7)得兩組解

相應的本征函數系分別為

其中n=1,2,3,4,··· ,i=1,2,3,4.

4.辛正交性與完備性

定理4.1設空間X=L2[0,a]×L2[0,a]×L2[0,a]×L2[0,a],則無窮維Hamilton 算子H的本征函數系{Xi(x),Xni(x)|i= 1,2,3,4;n=±1,±2,±3,±4,···}在Hilbert 空間X中具有辛正交性.

證 通過符號計算,可驗證本征函數系{Xi(x),Xni(x)|i=1,2,3,4;n=±1,±2,±3,±4,···}滿足:

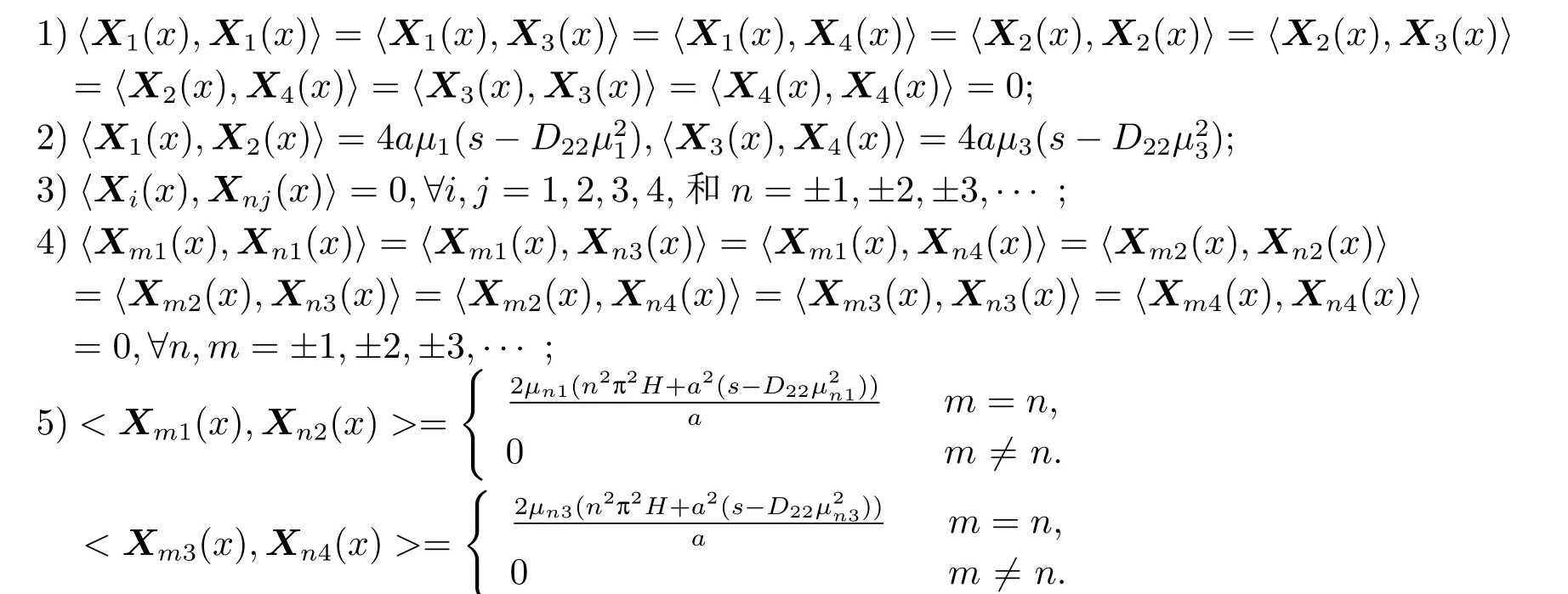
因此,定理4.1得證.

定理4.2在Hilbert 空間X中,無窮維Hamilton 算子H的本征函數系{Xi(x),Xni(x)|i=1,2,3,4;n=±1,±2,±3,±4,···}在Cauchy 主值意義下是完備的.

證?F(x) = (f1(x),f2(x),f3(x),f4(x))T∈X,在Cauchy 主值意義下,用辛本征函數系{Xi(x),Xni(x)|i=1,2,3,4;n=±1,±2,±3,±4,···}可展開為如下辛-Fourier 級數

其中

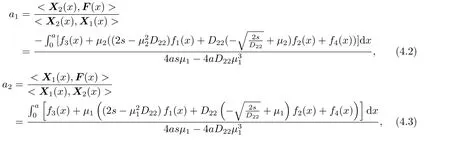
通過符號計算得到

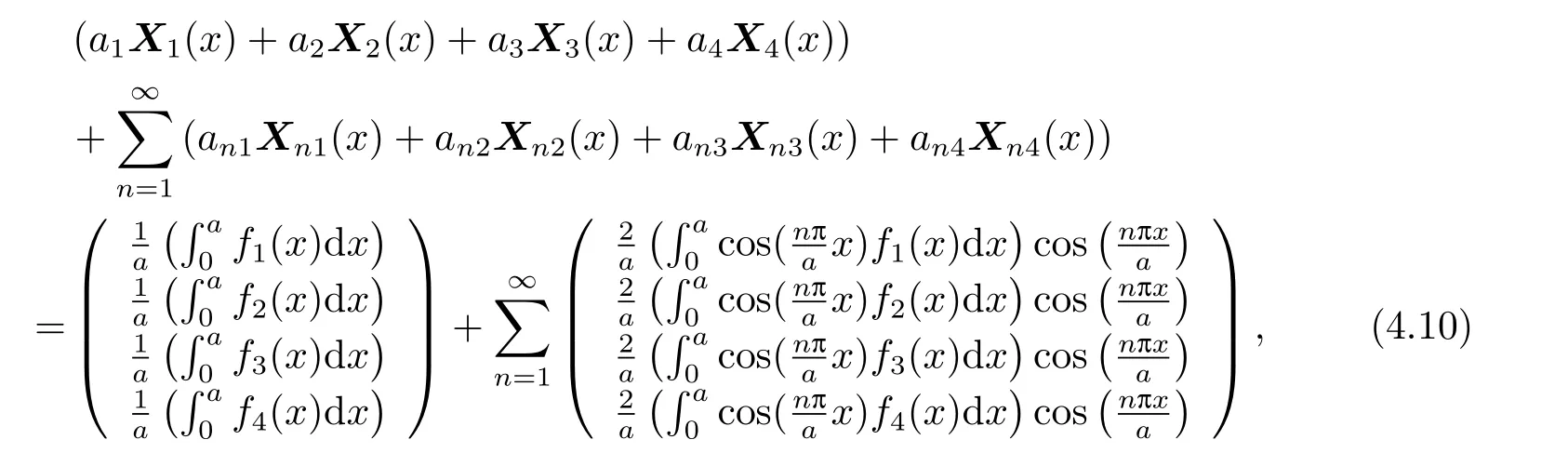
因此,定理4.2得證.

5.通解

設非齊次項f=(0,0,q,0)T可展開為

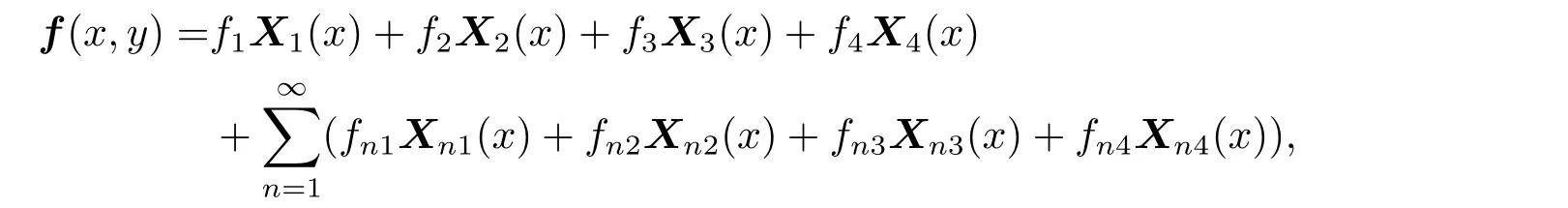
根據本征函數系的辛正交性可得

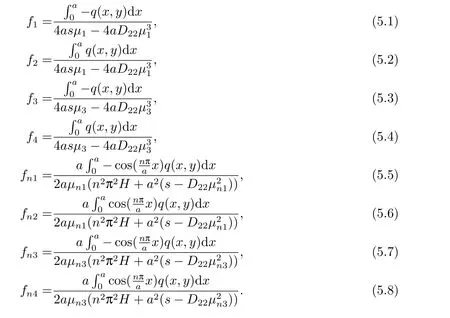
設在對邊滑支條件下Hamilton 系統(2.2)的解為

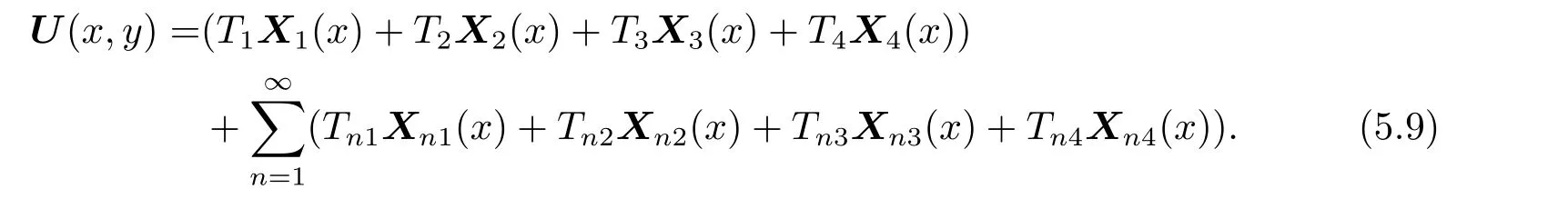
根據本征函數系的辛正交性有

其中Ci,Cni(i=1,2,3,4)為待定常數.

將式(5.10)代回式(5.9)可得

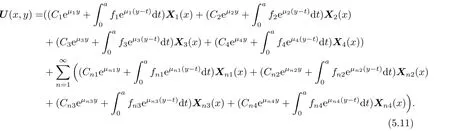
由此可得集中荷載下正交各向異性矩形薄板在對邊滑支條件下的一般解

其中H(y ?y0)是Heaviside theta函數.

6.算例

例1考慮雙參數彈性地基上正交各向異性矩形薄板四邊滑支的彎曲問題,在(x0,y0)處有集中荷載P,在y=0 和y=b處邊界條件是

其中

由通解(5.12)和邊界(6.1)可得關于系數C1,C2,C3,C4和Cn1,Cn2,Cn3,Cn4的聯立方程組,解得

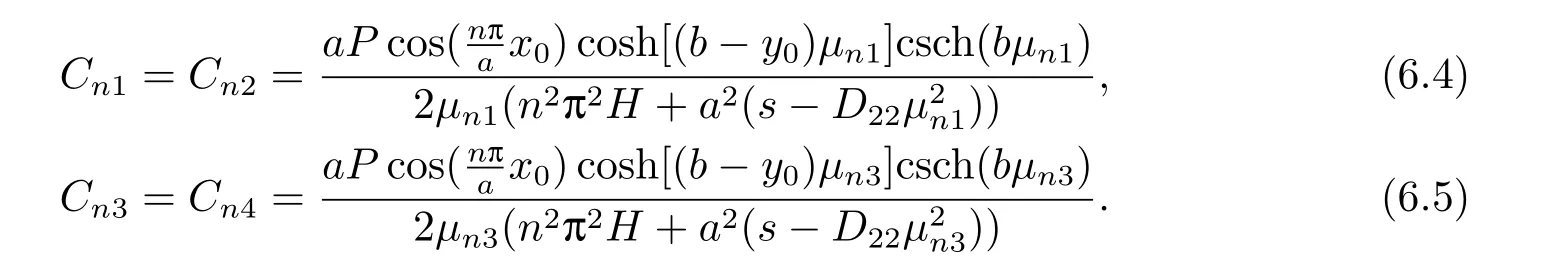
將式(6.2)-(6.5)代入式(5.12)可得通解

當s=0 且D11=D22=D12+2D66時,對于四邊滑支矩形薄板的彎曲問題,所得到的一般解與文[14]結果一致.

7.結論

本文用辛本征函數展開法研究了雙參數彈性地基上正交各向異性矩形薄板的彎曲問題.求出對邊滑支問題所對應Hamilton 算子的本征值以及相應本征函數系,并證明Hamilton 算子本征函數系的辛正交性以及在Cauchy 主值意義下的完備性.根據本征函數系的完備性,得到了雙參數彈性地基上正交各向異性矩形薄板對邊滑支彎曲問題的一般解.本文所研究的內容顯然包括了無彈性地基(k= 0,s= 0)、單參數彈性地基(k= 0 或s= 0)以及雙參數彈性地基上各向同性矩形薄板(D11=D22=D12+2D66,υ12=υ21) 的彎曲問題.

本文所得本征函數系的完備性結論,為基于對邊滑支問題的辛疊加方法應用到正交各向異性矩形薄板的各類邊值問題中提供了理論基礎.