十進制整數編碼的DE算法模式集定理研究

王凱光,高岳林

(北方民族大學數學與信息科學學院,寧夏 銀川750021)

1.引言和預備知識

差分進化算法(Differential Eveolution,簡稱DE[1?3])是由Storn和Price于1995年提出的為解決切比雪夫不等式(Chebyshev Inequality)的一種采用浮點矢量編碼的在連續空間進行搜索的全局優化算法[4?6],是通過差分方式進行迭代搜索的全局性進化算法,具有簡單、易實現、收斂性好、魯棒性強等優點[7?13],但就算法尋優的本質上說,其大小如何影響種群多樣性的分布,進而影響算法的收斂性質[11,13],在理論機制上面尚未得到說明.鑒于此,本文將在二進制模式定理[14?15]研究基礎上,應用十進制編碼對DE算法的動力學機制進行初步研究,探索種群規模(NP)、收縮因子(F)、交叉概率(CR) 等控制參數對種群尋優的動力學機制,并提出相應的編碼規則以及基本概念,給出能夠很好解釋DE算法各類參數對種群尋優能力影響的十進制模式集定理.

ⅠDE算法原理

一般地,極小化優化問題如下表示:

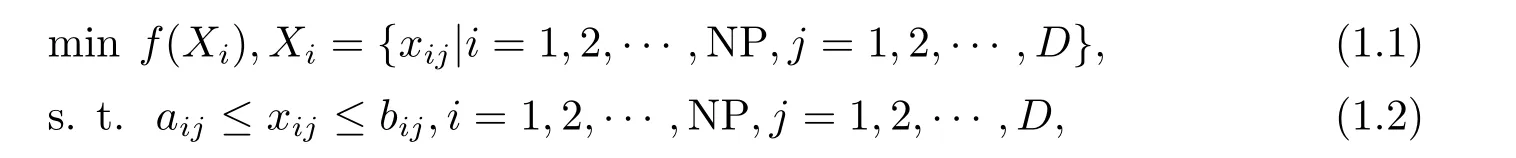
其中,D為決策變量的維數,NP為種群規模,f(Xi)為適應度函數,Xi(i=1,2,··· ,NP) 為D維參量矢量,xij(i= 1,2,··· ,NP;j= 1,2,··· ,D)為第i個個體的第j個分量,aij,bij分別為尋優范圍的下界和上界,差分進化算法(Differential Eveolution,DE)基本操作原理如下描述[1,4,7].

(i)初始化種群

設置DE算法的種群為X(t),則個體可表示為:

其中t為進化代數,NP為種群規模.

初始化種群:確定所求優化問題的維數D,最大進化代數T,種群規模NP,設置生成初值尋優向量如下所示:

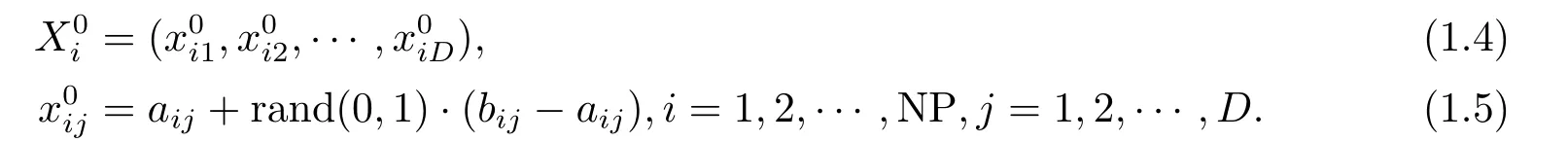
(ii)變異操作

DE算法的個體變異成分是父代個體的差分矢量,每次差分變異個體均來源于第t代父代個體種群中的兩個個體(Xti1,Xti2),其中i1,i2∈NP,則差分矢量定義為:Di1,2=Xti1?Xti2,那么對任意矢量個體Xti,定義變異操作為:

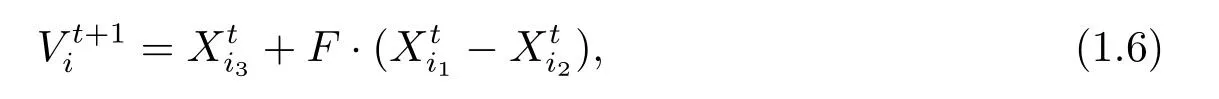
其中,i1,i2,i3∈{1,2,··· ,NP}且i1,i2,i3互不相同,種群規模NP≥4,F為收縮因子.在種群中隨機選取不為零的相異矢量,通過差分操作得到變異個體,變異個體將實現調整種群多樣性的可能.

(iii)交叉操作

對于種群目標矢量個體(xti),與變異個體進行交叉操作,產生試驗個體Uit+1,為保持種群多樣性,引入交叉概率CR和隨機函數rand(0,1)對變異個體和目標矢量個體(xti)進行交叉選擇,保證試驗個體至少有一位由變異個體貢獻,對于其他位點,通過交叉概率CR決定變異個體和目標矢量個體(xti)對試驗個體中某些位點的貢獻,交叉操作的試驗方程如下:

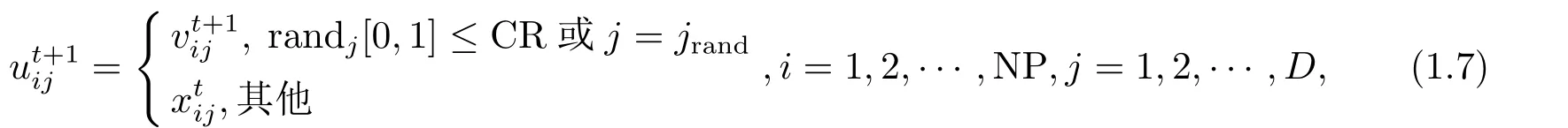
式(1.7)中randj[0,1],CR∈(0,1)為交叉概率,CR取值越大,表明矢量個體在不同位點發生交叉而產生新矢量個體的概率就越大;CR = 0時,表明沒有發生任何交叉操作,有利于保持種群的多樣性和全局群搜索能力;CR=1時,表明一定在某些位點發生交叉操作,有利于保持全局搜索和加快收斂速度.CR=0或1是發生交叉操作的兩種極端情況,j=jrand為隨機選擇的位點,這是為了試驗個體Uti要從變異個體V ti至少獲得一個發生基因變異的位點,確保變異個體目標矢量個體(xti)、試驗個體三者矢量個體之間互不相同,表明交叉操作引起種群間的交叉是有效交叉.

(iv)選擇操作

DE算法的選擇操作是一種基于貪婪算法的選擇機制,經過變異和選擇操作之后生成的試驗個體與目標矢量個體(xti)進行競爭和選擇,若當Uit+1的適應度值好于Xit的適應度值,那么作為最優個體會被種群繼承到下一代,否則保留到下一代的個體將是(xti),選擇算子在種群中的選擇作用由下述方程進行描述:

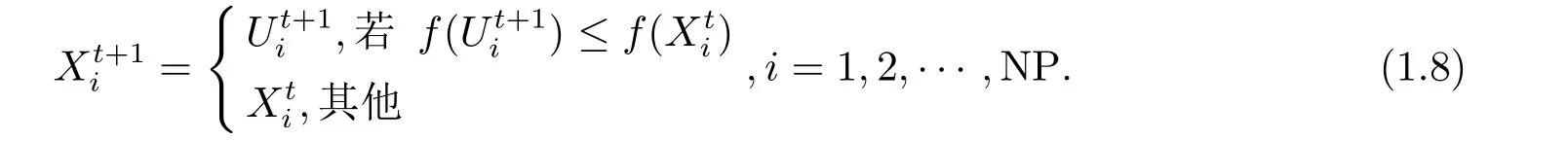
Ⅱ二進制編碼模式定理

引理1.1[14?15](模式定理,Schema Theorem) 在遺傳算子選擇、交叉、變異作用下,那些低階、短定義距、高適應度的模式的生存數量,將隨著迭代次數的增加而以指數級增長.

2.十進制編碼DE算法的模式集定理

對于十進制整數編碼的DE算法,采用V={0,1,2,3,4,5,6,7,8,9}10個基本字符作為基本字符串(Essential Character String),字符串中不確定位點(也稱為分配符)?均在10個基本字符中取值,基本字符串中若含有不確定位點?,則稱為普通字符串(Ordinary Character String),顯然基本字符串也屬于普通字符串(簡稱字符串(Character String)),字符串中任意字符的位點用{di|i ∈Z+,di ∈V}來表示.

Ⅰ基本概念及定義

定義2.1(模式,Schema)H稱之為一個模式,若存在形式={?,0,1,2,3,4,5,6,7,8,9},其中?的位點是任意的,并記作H=V,其中分配符?∈{0,1,2,3,4,5,6,7,8,9}.例如,H=?5?7??9就是一個模式,而H=0517119就是一個確定的模式表示形式.

定義2.2(模式集,Schema Sets)?稱之為一個模式集,若存在形式?={Hi|i ∈Z+}.

定義2.3(模式集階,Schema Sets Order) 包含在模式集?中所有模式{Hi|i ∈Z+}的階的總和,稱為模式集?的模式集階,記作Θ(?).若?Hi ∈?,O(Hi) =ki,則

例1現有一個模式集?={Hi|i ∈{1,2,3}},其中,O(Hi) =ki,i ∈{1,2,3},那么,也即這個模式集?的階為說明此時該模式集?中3個相異個體分別包含各自模式{Hi|i= 1,2,3}的階ki,那么這三個模式{Hi|i= 1,2,3}的階的總和為

注 由于一個種群規模為NP的種群,假設其中存在有限個模式的個體,相異模式個體所攜帶的表示其特征量的模式是相異的,采用{Hi|i ∈Z+}作為模式集階的基本量是基于以下考慮:假設這里有兩個相異模式的個體(此時模式和個體是相當的)H1、H2,O(H1)=k1,O(H2)=k2,即這兩個模式個體所攜帶的染色體(確定字符串)上的不同位點上基因(確定字符)的個數分別為k1,k2,經過選擇、交叉、變異后所得新個體中染色體(新確定字符)上的位點會增加或者說新的確定子字符個數會增加,按照遺傳算法模式定理,新增加的確定字符個數將介于min{k1,k2}和ki之間,或者說新個體的多樣性特征會增加與兩父代個體不同的某些特征,鑒于種群進化的不確定性,采用{Hi|i ∈Z+}作為模式集階的基本量,具有概率上的廣義特征.

定義2.4(模式集串長,String Length of Schema Sets Order) 模式集?中所有模式{Hi|i ∈Z+}包含的所有字符的數量為l,則稱該模式集?的串長為l,并記作L(?)=l.

例2若?={Hi|i= 1,2},L(H1) =l1,L(H2) =l2,則L(?) =L(H1)+L(H2) =l1+l2,也即這個模式集?的串長為L(?) =L(H1)+L(H2) =l1+l2,說明此時該模式集?中2個相異個體分別包含各自模式{Hi|i= 1,2,3}的串長li,那么兩個模式{Hi|i= 1,2,3}的串長總和為L(?)=l1+l2,模式集?的串長對相異模式個體的變異強度有概率上被分割或替換的可能性,串長越長,這樣的可能性就越大,反之越小.

定義2.5(模式集距,Schema Sets Order Range) 模式集?中所有模式{Hi|i ∈Z+}進行降序或升序排列,模式{Hi|i ∈Z+}按次序排列的第一個模式的第一個位點上的確定字符(按次序方向)與按次序排列的最后一個模式的最后一個位點上的確定字符(按次序方向)的距離,稱為模式集距,記作δ(?).

例3現有模式集?={Hi|i= 1,2},其中H1=?2??4,H2=?2?5?,將該模式集的基本量按順序排列,對于模式集的第一個基本量H1,按順次序排列的第一個確定字符為2,其確定為點為第2位點,同樣模式集的第二個基本量H2,按順次序排列的最后一個確定字符為5,其確定位點為第9位點,那么該模式集?距為δ(?)=9?2=7,同模式集串長的概率意義類似,不同的是模式集距中若有位點被分割或替換,發生變異的可能性強于模式集串長.

定義2.6(平均適應度函數,Function of Average Fitness) 設X(t)={Xt1,Xt2··· ,XtNP}為第t代種群,Ev(Xti)為Xti的適應度,則稱

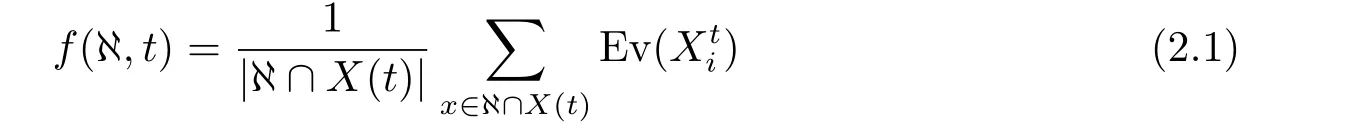
為模式集?的平均適應度函數.

其中,Ev(Xti)是種群規模為NP的種群中,任意個體(既包含同一模式的個體,也包含相異模式的個體,總之是所有種群個體)的平均適應度,f(?,t) 是種群規模為NP的種群所包含的相異模式個體的平均適應度,二者具有檢索個體數量上的不同,但其數學性質完全類似.

ⅡDE算法的模式集定理

文[16-18]介紹了標準的遺傳算法的基本模式定理,Whitley教授[19?20]將二進制編碼的字符串推廣到任意進制字符串編碼上,我們將在前人已有的研究基礎上對DE算法的模式集定理進行探討.我們知道,控制DE算法的各類參數主要有種群規模NP、收縮因子F、交叉概率CR.下面介紹十進制整數編碼DE算法的模式集定理,它將從動力學角度較為詳細地闡述DE算法的進化機理.

定理2.1設DE算法的交叉概率和收縮因子分別為CR和F,模式集?的距為δ(?),模式集?的階為Θ(?),第t+1代種群X(t+1)中含有?中元素個數的期望值記為E(?∩X(t+1)),則有

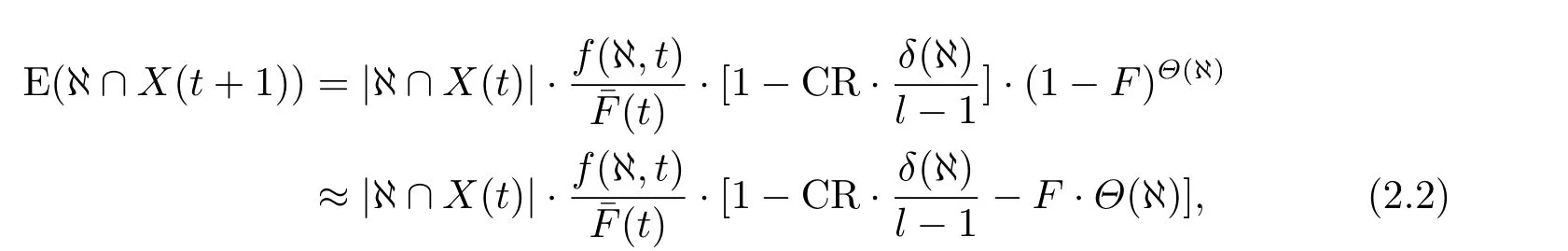
其中,l為X(t)所包含模式集?的串長.(t)=∑x∈?∩X(t)Ev(Xti)/|X(t)|,|?∩X(t)|為X(t)中含于模式集?的元素個數.

證 (i) 選擇操作對模式集?的生存數量的影響

假設種群規模為X={X1,X2,··· ,XNP},給定相應進化代數t,模式集?包含個數不大于種群規模為NP個相異的模式{Hi|i ∈NP},其適應度函數(或稱之為種群演化初始時模式集的平均適應度函數)記為f(?,t).按照進化算法演化次序,一個確定種群規模NP的種群,模式集?中任一個體按照選擇操作被選擇的次數與其適應度函數成正比例關系,種群每演化一次,|?∩X(t)|中相異模式的每一個體被選擇的平均次數占種群規模中所有個體被選擇的平均比例數量為:

其中,

為證明方便,假設種群規模為NP的種群X={X1,X2,··· ,XNP},NP個數量的個體所攜帶的模式{Hi|i ∈NP}兩兩相異,?∩X(t) 中的個體數目|?∩X(t)|經過N次選擇,T為最大迭代次數,理論上期望在經過{t,t ≤T}次迭代后,模式集?在這樣的種群規模?∩X(t)內元素被選擇的次數的期望為:

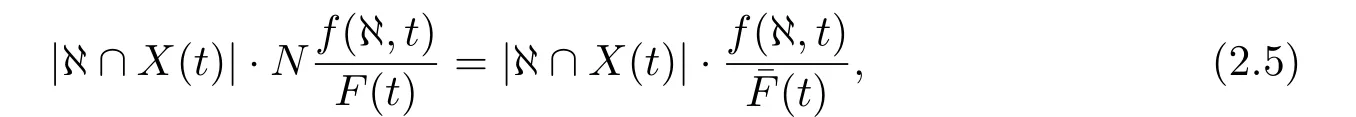
上式(2.5)說明下一代種群中模式集?的生存數量與模式集?的適應度函數值成正比,與群體X(t)平均適應度函數值成反比.可以分為兩種情況,一種是:當f(?,t)>ˉF(t)時,模式集?的生存數量增加.另一種是:當f(?,t)<ˉF(t)時,模式集?的生存數量衰減.由此可見,群體中任意模式集的生存數量都會在選擇操作中呈現如此變化規律.

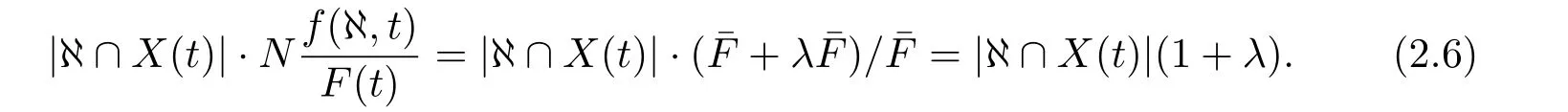
那么當群體從初始迭代值t= 0開始進行DE算法演化操作,假設λ這一常數不變,則上式(2.6)可改寫為:

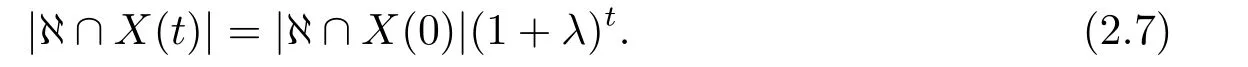
這表明,在選擇操作作用下,模式集?的生存數量是以指數形式進行演化的.分為兩種情況,一種情況是:當λ >0時,模式集?的生存數量以指數形式增加.另一種情況是:當λ <0時,模式集?的生存數量以指數形式衰減.但這樣的變化僅是描述了已有模式集?的生存數量的變化,并未在原有基礎上產生新的模式.

(ii) 交叉操作對模式集?的生存數量的影響

由于選擇操作不能檢索新的種群區域,為此增加交叉操作.這里采用單點交叉(這并不影響定理的證明).由于單點交叉時隨機選擇1到l ?1位點中某一位點作為交叉點,交換交叉位點之后的所有對應字符子串,當交叉操作作用在模式集?所包含所有模式{Hi|i ∈NP}的定義距{li|i ∈NP}之內,模式集?有被破壞的可能,應該明確注意到,即使交叉操作作用在模式的定義距內部,模式集同樣存在不被破壞的可能.

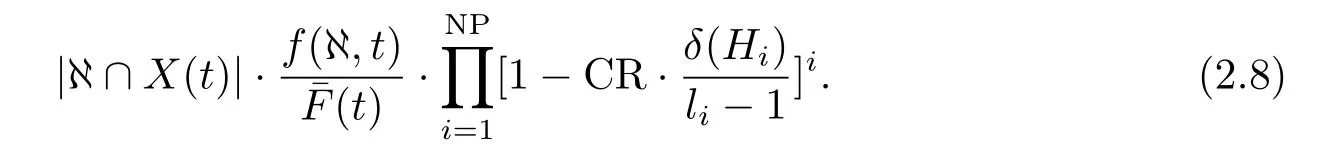
由上式(2.8)可以看出,定義距δ(Hi)越大,模式被破壞的概率越大.一般地,對任意模式{Hi|i ∈NP}可以計算出經交叉操作后生存概率的下界為Psurvival,在單點操作作用下,任一長度為{li|i ∈NP}的模式的生存概率為那么,在交叉作用下模式集?存活概率(?存活估計值)為:

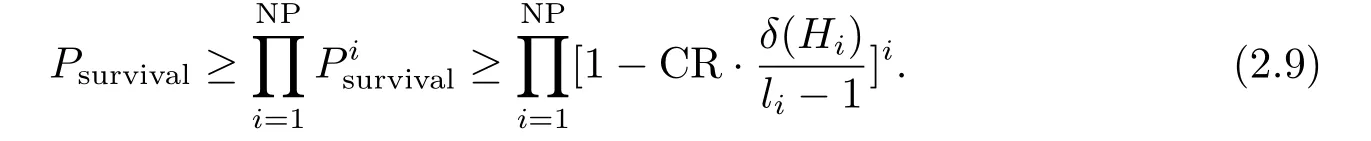
現考慮模式集?在選擇和交叉兩種操作用下的生存數量有如下估計式:

這表明,模式集?增加或衰減依賴于平均適應度函數值以及定義距δ(Hi).當f(?,t)>(t)且δ(Hi)較小時,模式集?的生存數量呈現指數級增長.反之,呈現指數級衰減.

(iii) 收縮因子F對模式集?的生存數量的影響

DE算法是以差分形式V t+1i=Xti3+F ·(Xti1?Xti2)進行變異的,其中F類似于進化算法中的變異概率,則對任一模式{Hi|i ∈NP}的每一位點發生變異的概率為F,那么該位點不發生變異的概率為1?F,若每一模式Hi在變異操作作用下能夠生存下來(即Hi不受破壞),也就意味著該模式Hi確定位點上的字符在變異時不能發生任何變化,又因為模式Hi的階為O(Hi),則在變異操作作用下模式Hi不被破壞的概率為(1?F)O(Hi),從而模式集?在變異操作作用下不被破壞的概率為或者寫成(1?F)Θ(?),它們之間是等價的關系.

綜上所述,經過選擇,交叉,變異操作后,X(t+1)含有模式集?中元素的個數期望值如下式所示:

同時,由于收縮因子與變異概率在種群中個體的作用上是相當的,假設種群規模為NP的種群X(t) ={Xi(t)|i ∈{1,2,··· ,NP}}中每一個體的變異概率為{Pi|i ∈{1,2,··· ,NP};Pi ∈(0,1)},在種群規模為NP的種群X(t)中,任取三個相異個體{Xij|j=1,2,3},于是將(1.6) 式可改寫為如下式子:

由于相異個體{Xij|j= 1,2,3}所屬模式{Hij|j= 1,2,3}也是相異的,同樣地,三個相異個體的變異概率{Pi|i ∈{1,2,3};Pi ∈(0,1)}是隨機相異的,因而模式{Hij|j= 1,2,3}關于下一代模式和變異概率分別滿足下式:

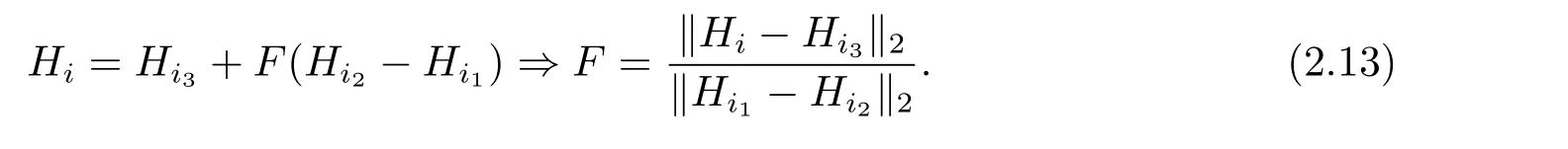
同樣地,

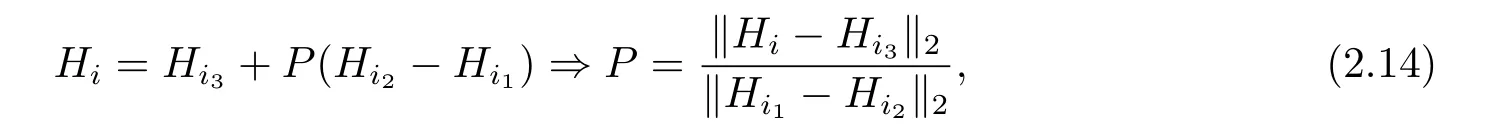
其中,這里的P是一個理論上的具有概率特征的數學量,在算子操作作用下起到改變個體編碼數值的作用,但僅僅是一種改變具體數值編碼的可能性,在尋優過程中,由于自然環境或是其它影響因素,這種概率上的改變會更加明顯,最終使得個體的數值編碼發生改變,從而產生個體變異,實現進一步交叉和選擇的可能,為產生新的尋優個體提供客觀條件.在實際操作中應該對于不同模式{Hij|j=1,2,3}的變異概率,也即如下式子:

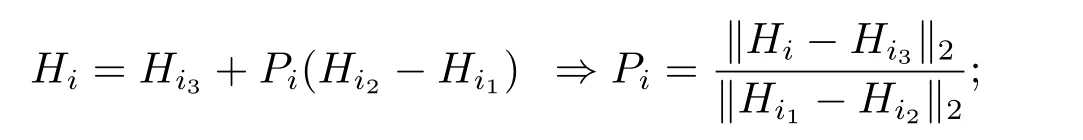
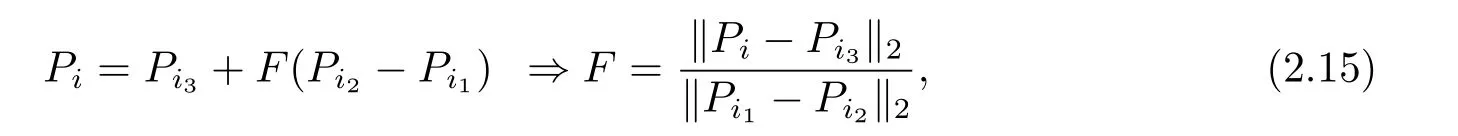
其中上面兩式在理論說明上是等價的,由此可得,

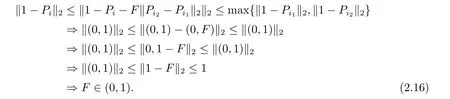
當F <1,CR<1時,(1?F)Θ(?)≈1?F ·Θ(?),且

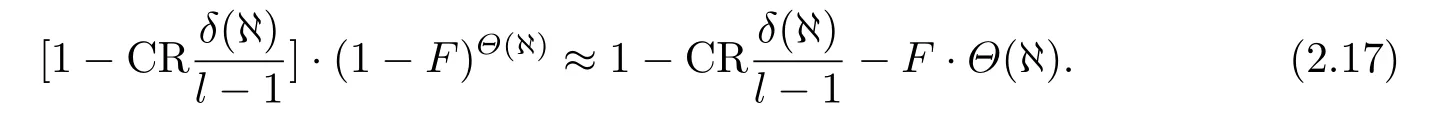
注意到(2.17)式以及選擇、變異、交叉三種算子對模式集?中所有模式{Hi(t)|i ∈{1,2,··· ,NP}}的生存數量的分析,可以得出以下結論:

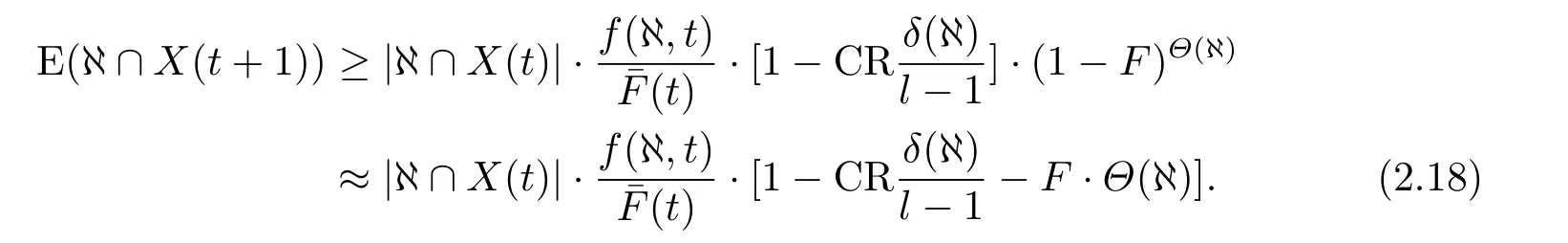
結論成立.

定理2.2(模式集定理) 對DE算法進行十進制整數編碼,在DE選擇、交叉、變異操作作用下,具有較低模式集階、較短模式集距、較高適應度函數值的模式集的生存數量,隨種群迭代次數的增加呈現指數級增長.

推論2.1在DE算法中,低階、短距且適應度函數值高于平均適應度函數值的模式集?,在子代種群中的數量期望值以指數形式增加.

推論2.2在定理2.1證明過程中,有效地縮減了收縮因子的變化范圍,將F的變化范圍在理論上縮小到(0,1)區間,同時也體現了收縮因子與變異概率在種群演化過程中具有概率上的相當性特征,和Storn教授與Price教授在文[1]中對F的取值為0.5左右吻合,與文[21-26]將F均取值為(0,1)區間高度吻合.

推論2.3在種群規模為NP的種群中,適應度函數值高于平均適應度函數值的模式集?中任意模式{Hi|i ∈{1,2,··· ,NP}}將會按照指數級增長方式被選擇.

3.結語

本文基于十進制整數編碼基礎上嘗試在理論層面推導出選擇、交叉、變異等操作算子在推動種群演化、種群尋優的模式集定理(即DE算法推動種群演化的動力學機制),研究結論表明,在DE選擇、交叉、變異等操作算子作用下,具有較低模式集階、較短模式集距、較高適應度函數值的模式集的生存數量,將隨種群迭代次數的增加呈現指數級增長.該定理從根本上說明了差分進化算法(Differential Eveolution,簡稱DE)在推動種群尋優的動力學機制,有效解決了離散種群個體在全局尋優方面的動力學演化機制,為后續研究連續型種群個體的動力學演化機制提供了研究基礎.在研究之余,我們隱約感覺到在生物學意義上的閉生態種群中的個體具有量子特征,至于這樣的量子特征在尋優過程是如何體現的,以及體現出來的是何種量子特征,還有待于進一步研究和討論.同時還研究了收縮因子F與變異概率的相當性特征,將收縮因子F的范圍縮小至(0,1)區間.本文提出的十進制整數編碼DE算法的模式定理在理論層面較好解釋了種群演化的內部動力學機制.