一類帶Hardy-Sobolev臨界指數的非局部問題正解的存在性

王躍,葉紅艷,索洪敏

(貴州民族大學數據科學與信息工程學院,貴州 貴陽550025)

1.引言和主要結果

本文研究如下一類帶Hardy-Sobolev 臨界指數的非局部問題

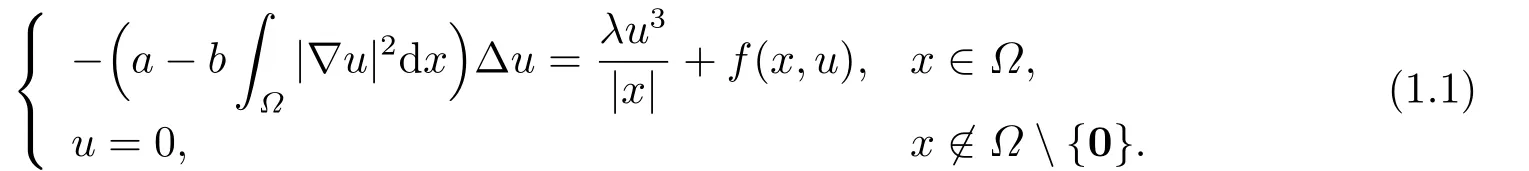
其中?是R3中的光滑有界域,常數a,b>0,參數λ>0,f(x,u) 是?×R 到R 的連續函數.

含Hardy-Sobolev 臨界指數的問題在國內外已有大量的研究成果.例如,問題

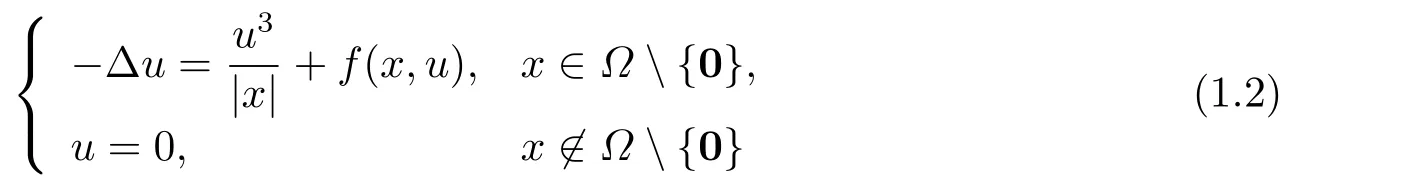
正解的存在性在[1-3]等文獻中都有研究,?通常是RN中的光滑有界域或等于RN(N是正整數).當取a=λ=1,b=0時,問題(1.2)便成問題(1.1)的一種特殊情形,因此問題(1.1)在理論上具有一定的研究意義.更多帶有Hardy-Sobolev臨界指數時正解的存在性及多重性問題的最新研究還可以從文[4-6]及其引用文獻中找到.另一方面,問題

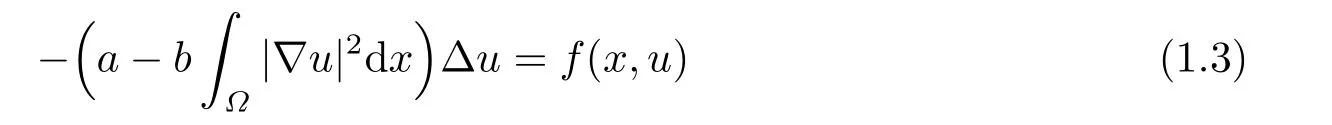
仍然含有非局部項.通過文獻檢索,Dirichlet 邊界條件下問題(1.3) 的研究近年來很受關注.如文[7]通過變分方法和山路引理獲得f(x,u) =|u|p?2u時非平凡非正解和非平凡非負解的存在性,其中? ?RN是光滑有界域,N ≥3 時N= 1,2時2?= +∞;文[8]考慮了f(x,u) =fλ(x)|u|p?2u時解的多重性,其中? ?RN(N ≥3) 是光滑有界域,文中獲得fλ(x)∈L∞且1

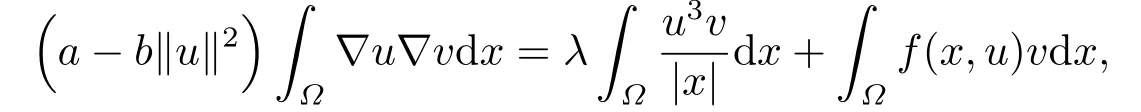
則把u定義為問題(1.1)的弱解(簡稱解),其中? ?u?vdx=?u,v?表示H10(?) 上的內積,本文的主要結果如下:

定理1假設a,b,λ>0 且f(x,u) 滿足如下條件:

(f1)如果f(x,u)≥0且存在s<5使對x ∈?一致成立;

(f2)存在μ>4使|u|>0時對x ∈?有那么,問題(1.1)至少有一個正解.

2.預備知識

考慮泛函

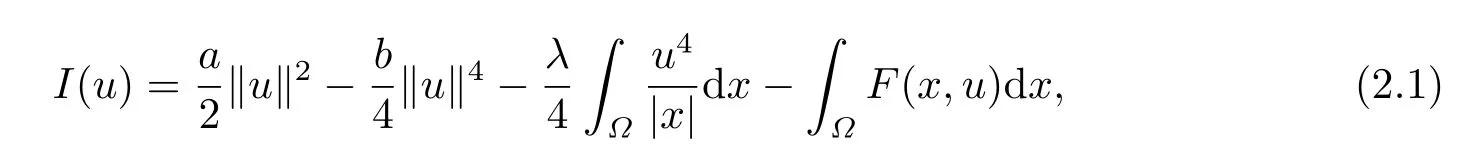
則對任意的v ∈H10(?) 有

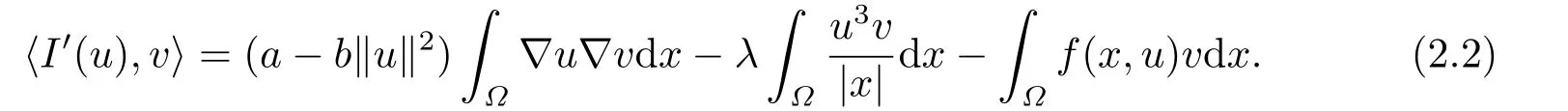
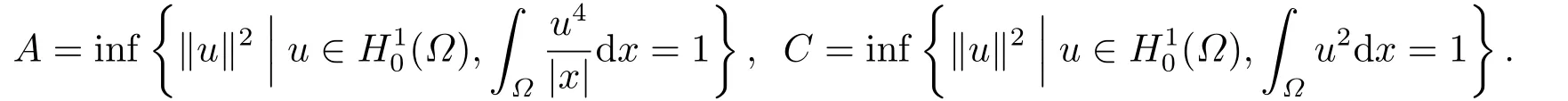
根據文[3]中定理3.1可知?= R3時A可取到.通過截斷技巧直接計算可得,對任意的正實數ε都存在對應的函數及正常數C1,C2,C3滿足

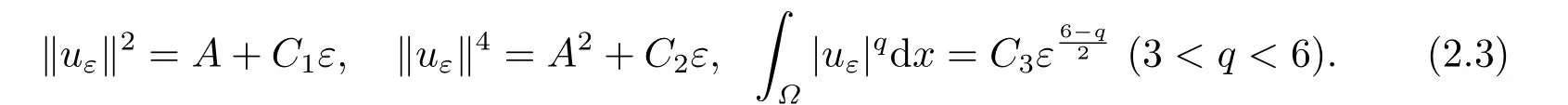
引理2.1若a,b,λ>0,(f1)和(f2)成立,那么對任意I滿足(PS)c條件.

證設{un}是I的(PS)c序列,則有

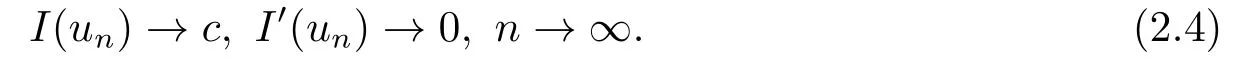
再由條件(f2)有

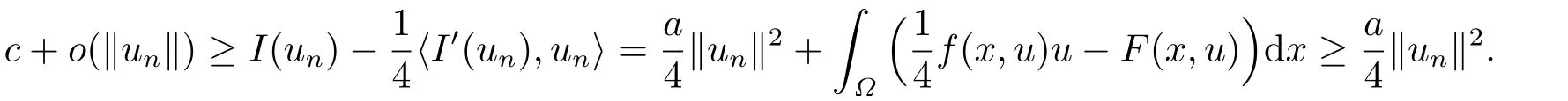
因此由Sobolev嵌入不等式可知{un}有界,從而存在u ∈H10(?) 及{un}的子列(不妨仍記為{un})使得n →∞時: 在H10(?)中un ?u;在Lp(?)(1≤p <6)中un →u;對任意x ∈?,幾乎處處有un(x)→u(x).由(f1),對任意ε>0,存在常數mε,M >0,sε >s+1 使得

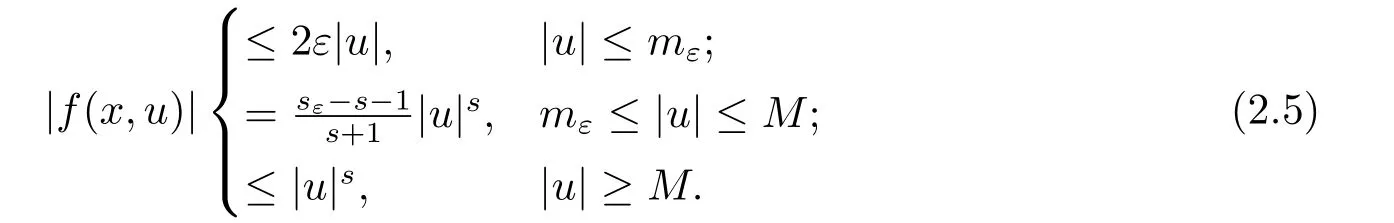
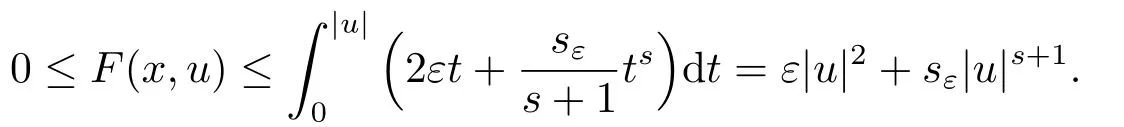
根據un ?u和Lebesgue 控制收斂定理(文[……