A Similarity Transformation and the Decay Mode Solutions for Three-Dimensional Cylindrical Kadomtsev-Petviashvili Equation

ZHANG Jinliang(張金良),WANG Fei(王飛)

( School of Mathematics and Statistcs,Henan University of Science and Technology,Luoyang 471023,China)

Abstract: In this paper,a similarity transformation between the solutions of three-dimensional cylindrical Kadomtsev-Petviashvili equation and the solutions of threedimensional Kadomtsev-Petviashvili equation with constant coefficients is firstly derived,and the corresponding constraint conditions for the coefficients of three-dimensional cylindrical Kadomtsev-Petviashvili equations are obtained.Then the exact solutions of the three-dimensional cylindrical Kadomtsev-Petviashvili equation are expressed by the similarity transformation and the solutions of the three-dimensional Kadomtsev-Petviashvili equation with constant coefficients.Lastly,four special three-dimensional cylindrical Kadomtsev-Petviashvili equations are studied,especially,the decay mode solutions of these three-dimensional cylindrical Kadomtsev-Petviashvili equations are obtained.

Key words: The three-dimensional cylindrical Kadomtsev-Petviashvili equation;The three-dimensional Kadomtsev-Petviashvili equation;Similarity transformation;Decay mode solution

1.Introduction

The cylindrical Kadomtsev-Petviashvili equation (CKP) in the form

was introduced by Johnson[1?2]to describe surface wave in a shallow incompressible fluid.The CKP (1.1) for magnetized plasmas with pressure effects and transverse perturbations in cylindrical geometry was also derived by using the small amplitude perturbation expansion method[3].And Eq.(1.1) is a (2+1)-dimensional generalization of the cylindrical KdV equation (CKdV)[4?5]

Due to the importance and wide application,CKP(1.1)has been paid attention by many researchers in mathematical physics.For instance,In[6],Klein et al.have shown that the Lax pair corresponding KP and CKP equation are gauge equivalent,and some class of solutions(Such as horseshoelike-front solutions,lump solutions and rational solutions) were obtained by using Darboux transformation approach.In [7],DENG has shown that the decay mode solution for CKP (1.1) can be obtained by B¨acklund transformation and Hirota’s method.

In [8-9],the reductive perturbation method is employed to derive a three-dimensional cylindrical Kadomtsev-Petviashvili (3D-CKP) equation

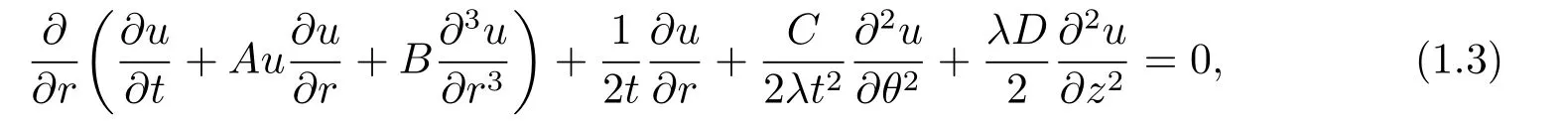
which is used to describe the non-planar ion-acoustic waves in positive-negative ion plasmas with stationary dust particles,the generalized expansion method is used to solve analytically the evolution equation,and a train of well-separated bell-shaped periodic pulses which can change to solitary pulses at certain conditions are obtained.In this paper,the 3D-CKP (1.3)will be considered.

The paper is organized as follows: In Section 2,we derive a similarity transformation[10–13]and the constraint condition for 3D-CKP (1.3);In Section 3,some special types of 3D-CKP are studied,and the decay mode solutions are derived.

2.The Derivation of Similarity Transformation

Suppose that the exact solutions of Eq.(1.3) are in the forms

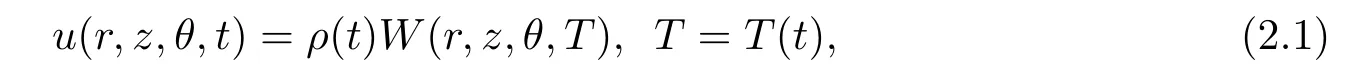
whereρ(t),T(t) are determined later,andW(r,z,θ,T) satisfy three dimensional Kadomtsev-Petviashvili (3D-KP) equation with constant coefficients

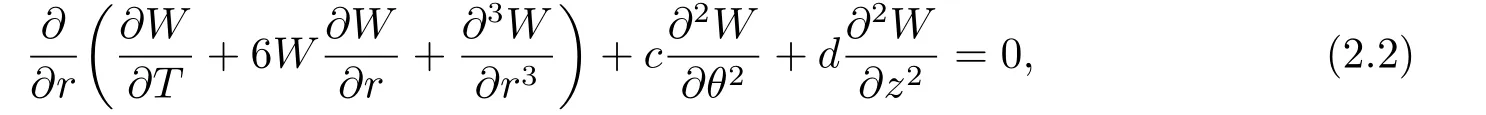
wherec,dare constants.From (2.1) we have

Substituting(2.1),(2.3)-(2.5)into the left hand side of system(1.3)and considering(2.2)simultaneously,yields

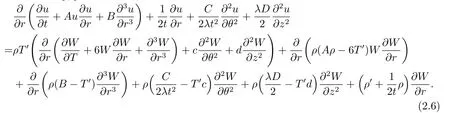
From (2.6),we obtain a set of partial differential equations

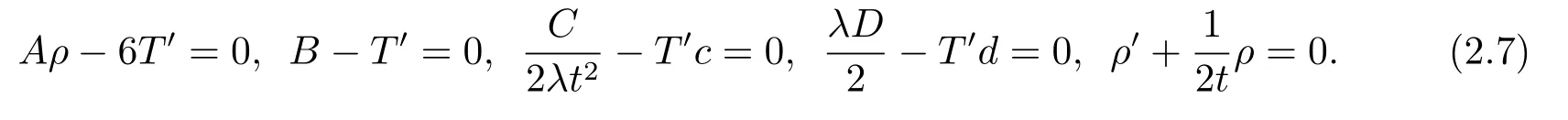
Solving these ODEs (2.7),we find the following expressions

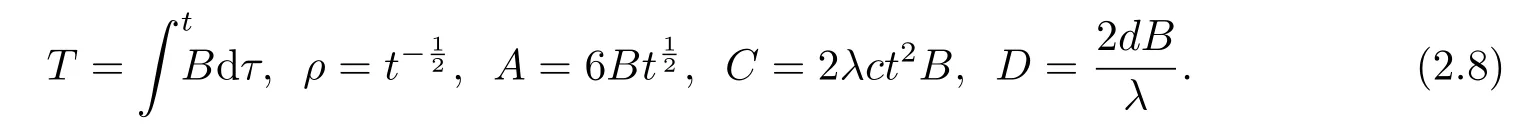
Then 3D-CKP (1.3) is rewritten as

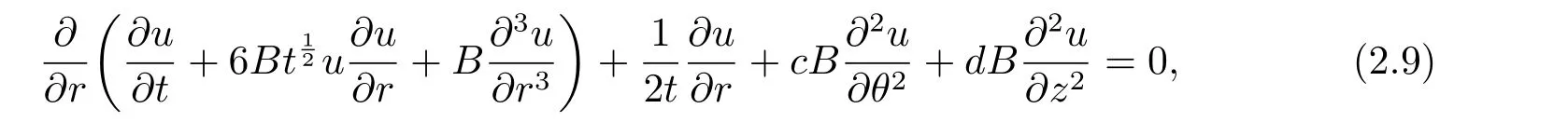
and similarity transformation (2.1) is rewritten as

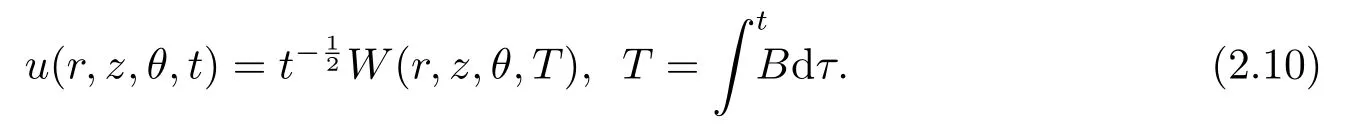
Using the similarity transformation(2.10)and the solutions of 3D-KP(2.2),we can easily obtain the solutions of 3D-CKP (2.9).

3.Some Special Type of 3D-CKP (2.9) and the Decay Mode Solutions

In this section,we consider some special type of 3D-CKP (2.9).

1) Cylindrical KdV equation with variable coefficients and the decay mode solutions.Settingc=d=0 in Eq.(2.9)yields a cylindrical KdV equation with variable coefficients

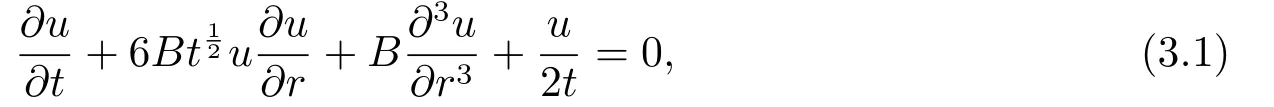
and 3D-KP (2.2) becomes a KdV equation with constant coefficients

From [14],some special soliton solutions of KdV (3.2) are listed as follows.One soliton:

Two soliton:

whereξj=kjr+ωjT,ωj=?k3j(j=1,2),eA12=

Three soliton:

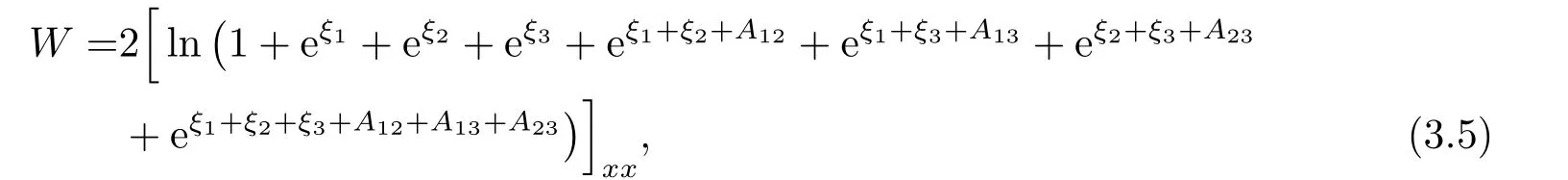
where

Using the similarity transformation(2.10)and the solutions above,the decay mode soliton solutions of cylindrical KdV equation with variable coefficients (3.1) are obtained as follows.

One decay mode soliton:

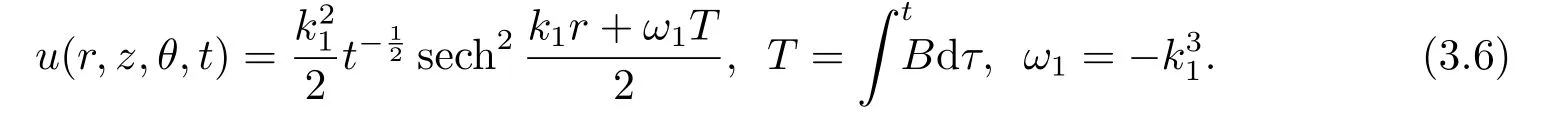
Two decay mode soliton:

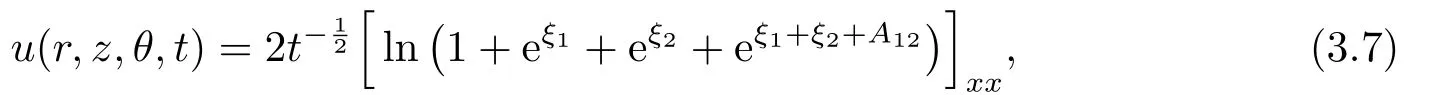
where

Three decay mode soliton:

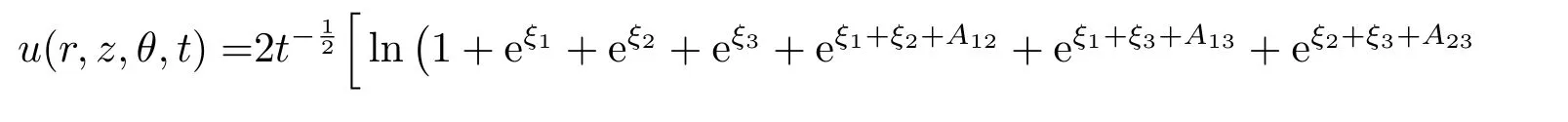
where

Note 3.1The decay mode multi-soliton solutions of Eq.(3.1) can be obtained using the results in [14].

2) Two-dimensional cylindrical Kadomtsev-Petviashvili (2D-CKP) equation and the decay mode solutions.

Settingc= 3σ2,d= 0 in Eq.(2.9) yields a two dimensional cylindrical Kadomtsev-Petviashvili (2D-CKP) equation

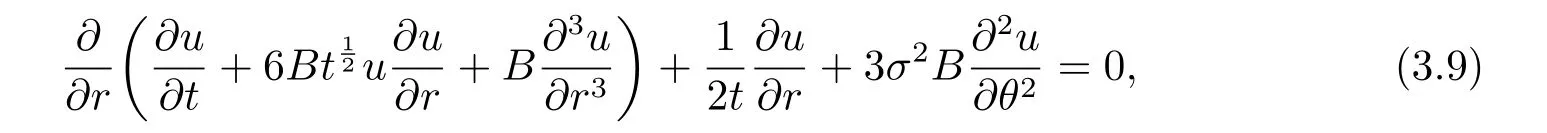
and 3D-KP (2.2) becomes Kadomtsev-Petviashvili equation with constant coefficients

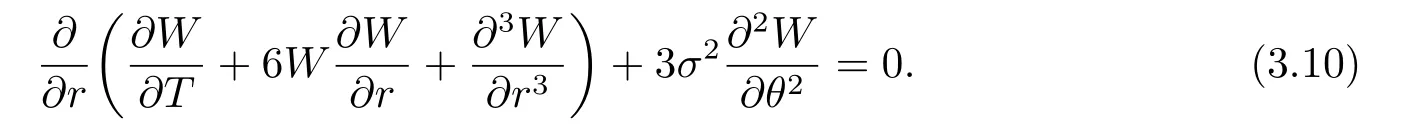
From [14],soliton solutions of KP (3.10) are listed as follows.

One-line soliton:

Two-line soliton:

where

Using the similarity transformation (2.10),the decay mode soliton solutions of twodimensional cylindrical Kadomtsev-Petviashvili(2D-CKP) equation(3.9)are obtained as follows.

One-line decay mode soliton:

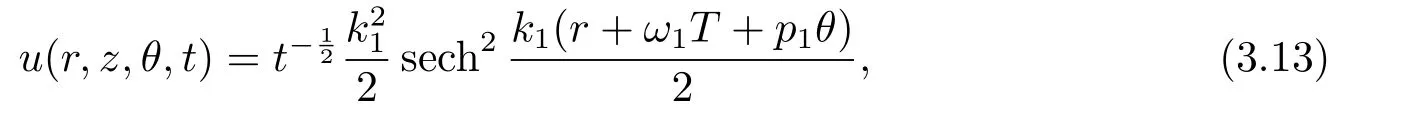
whereT=∫tBdτ,ω1=?k21?3σ2p21.

Two-line decay mode soliton:

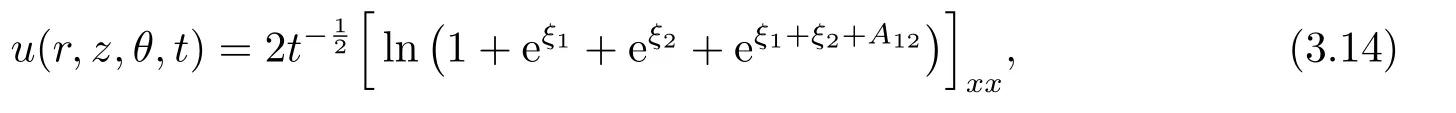
where

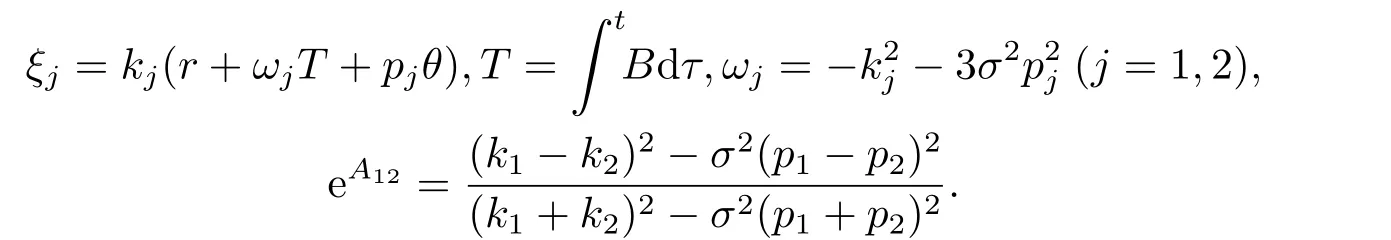
Note 3.2The decay mode multi-soliton solutions of Eq.(3.1) can be obtained using the results in [14].Here we omit it for simplicity.

3) First special three-dimensional cylindrical Kadomtsev-Petviashvili equation and the decay mode solutions.

SettingB=const in Eq.(2.9)yields a three dimensional cylindrical Kadomtsev-Petviashvili(3D-CKP) equation

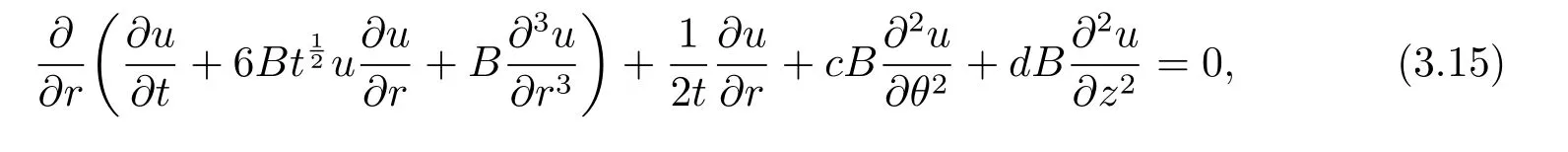
and 3D-KP (2.2) leads

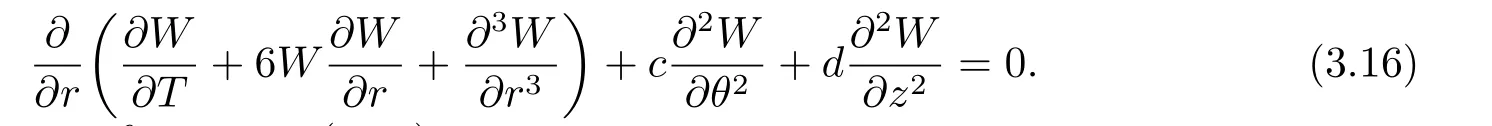
The similarity transformation (2.10) is rewritten as

Using the similarity transformation(3.17)and the travelling wave solutions of Eq.(3.16),the decay mode travelling wave solutions of Eq.(3.15) can obtained as follows.

Whenn+cm2+dl2<0,

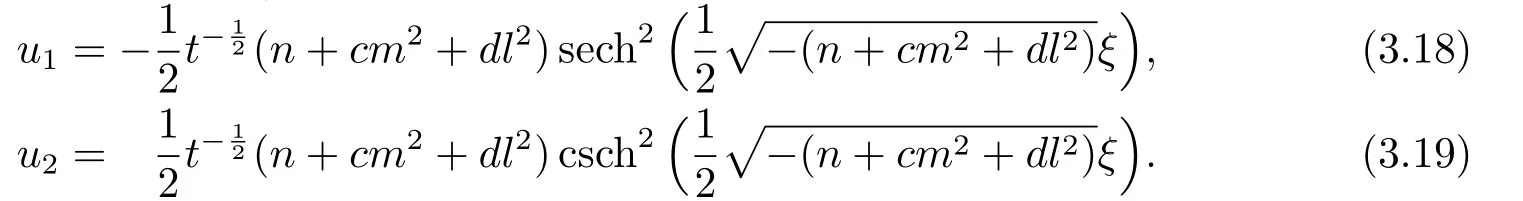
Whenn+cm2+dl2>0,

Whenn+cm2+dl2=0,

whereξ=r+lz+mθ+nBt,C1,C2,l,m,nare constants.

4)Second special three-dimensional cylindrical Kadomtsev-Petviashvili equation and the decay mode solutions.

Settingin Eq.(2.9)yields a three-dimensional cylindrical Kadomtsev-Petviashvili(3D-CKP) equation

The similarity transformation (2.10) is rewritten as

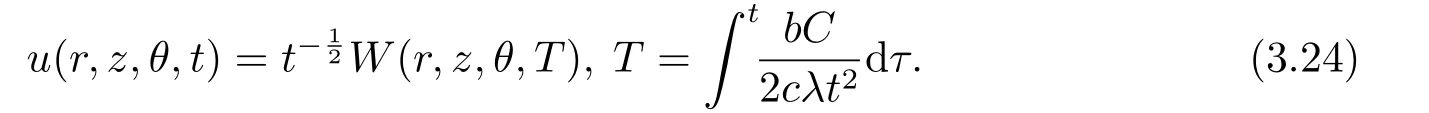
Ifb,C,c,λare constants,

Using the similarity transformation(3.24)and the travelling wave solutions of Eq.(3.16),the decay mode travelling wave solutions of Eq.(3.23) can obtained as follows.

Whenn+cm2+dl2<0,

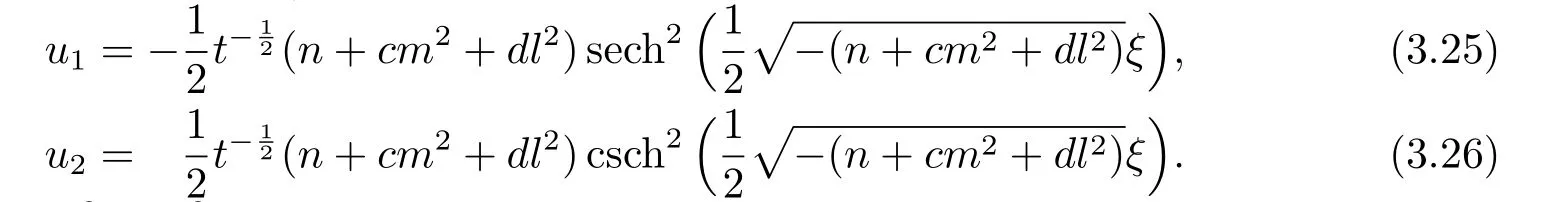
Whenn+cm2+dl2>0,

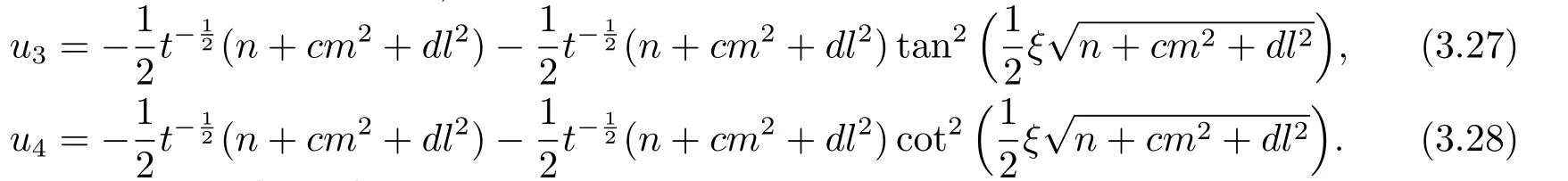
Whenn+cm2+dl2=0,

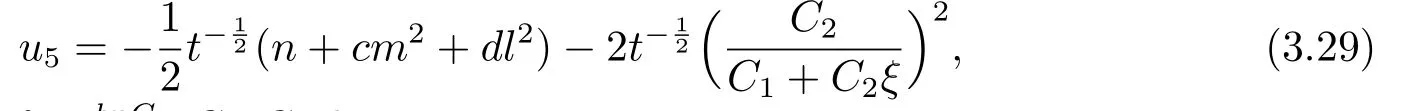
whereC1,C2,l,m,nare constants.

Note 3.3Except Eqs.(3.15) and (3.23),obviously,there exists other type of 3D-CKP(2.9).