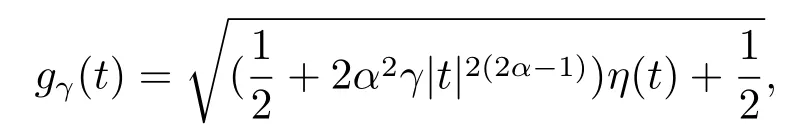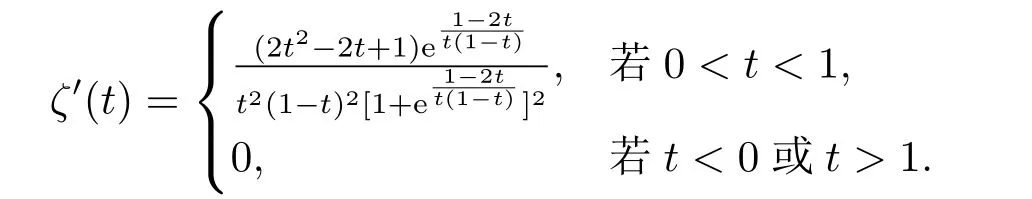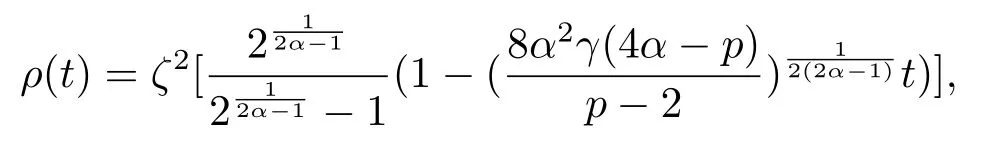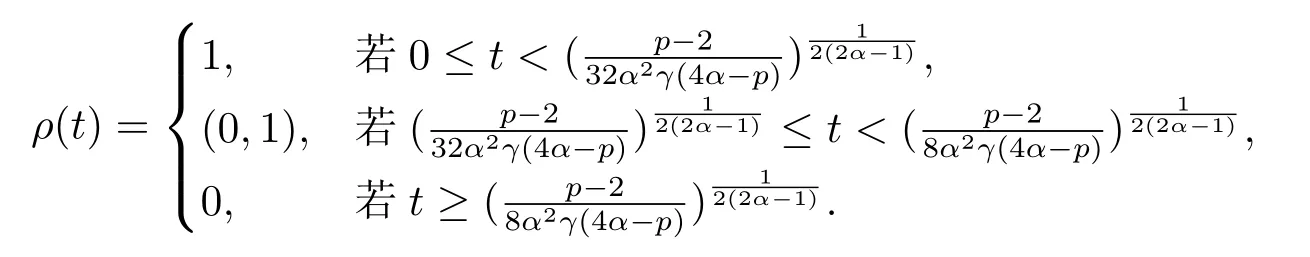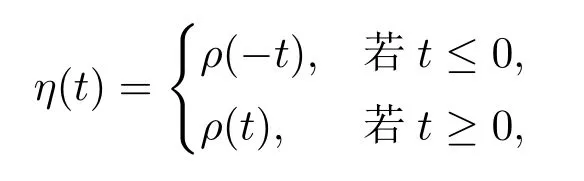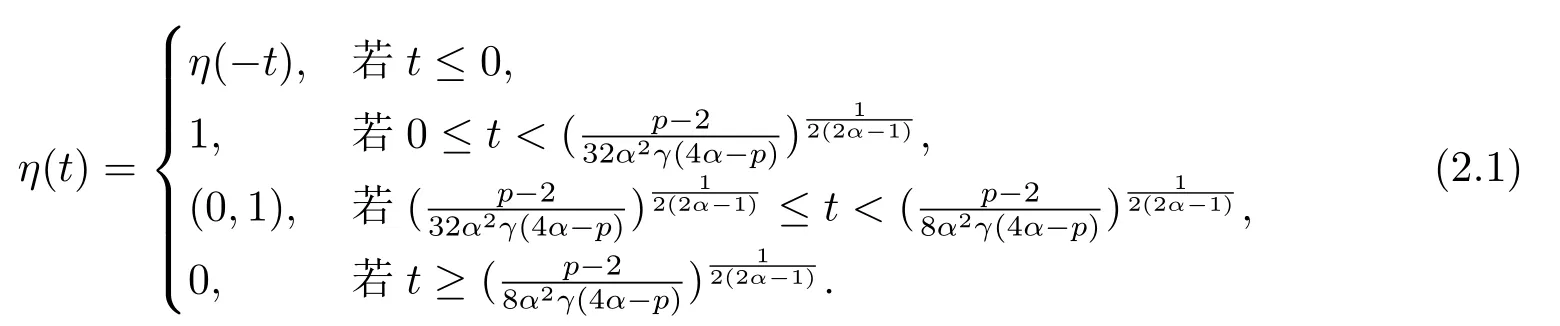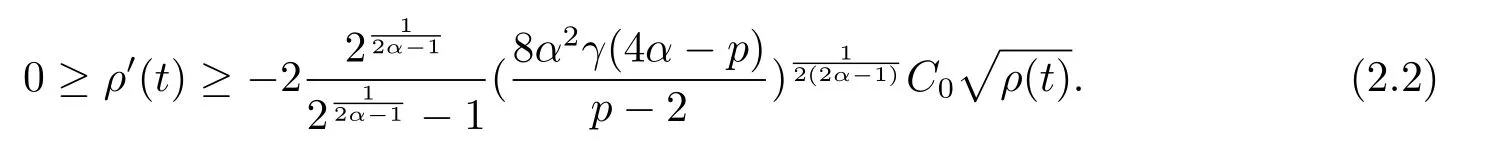含凹凸非線性項的一般擬線性橢圓方程解的存在性
張翔,潘文峰
(武漢理工大學數學系,湖北 武漢430070)
1.引言
在本文中,我們研究一類擬線性橢圓方程解的存在性,其表達式如下:
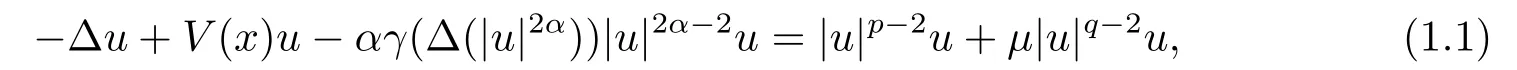
方程(1.1)來自于等離子體物理學中的超流薄膜方程,詳情可見文[7-8,12]以及更多關于物理背景的參考文獻.近幾年,在文[1,3,6-7,12-16]中,對于當α= 1 且μ= 0時的方程(1.1)解的存在性進行了廣泛的研究.而當μ >0時,在文[20]中,其主要的存在結果是通過約束極小化參數得到的.在文[13]中,先通過變量替換將擬線性問題(1.1)轉化成半線性問題,然后應用山路引理,構建一個Orilicz空間框架來證明正解的存在性.此外,通過應用變換替換,文[2,4,10]對于一般情況下的方程(1.1)也進行了深入的研究.與一般半線性橢圓方程相比,(?(|u|2α))|u|2α?2u的存在使得方程(1.1)更具挑戰性.在文[18]中,對于γ= 1時的方程(1.1),YANG等應用文[15]中的變量替換和文[5]中截斷函數方法,然后通過臨界點理論證明了在4α 在本文中,我們應用文[5,15-16]中的方法,研究方程(1.1)在的情況下解的存在性,并且我們將指數條件延伸到了2到2α之間. 我們假設位勢函數V滿足 關于方程(1.1)解的存在性,我們有如下結果: 定理1.1假設位勢函數滿足條件(V1),并且則存在一個γ0,使得當γ ∈(0,γ0)時,方程(1.1)存在一個正解uγ(x),且此解滿足: 當p ∈(2,2?)時,我們定義一個輔助函數gγ(t) : R→R+,如下: 其中η(t)∈C∞0(R,[0,1]) 是一個截斷函數. 首先,我們能夠建立一個適當的截斷函數ζ(t),令 然后可得ζ(t)∈C∞(R,[0,1]),0≤ζ(t)≤1,并且有 令ζ′(0) =ζ′(1) = 0,可得ζ′(0)≥0在[0,1]上一致有界.因此,存在一個C0>0,使得對于任意t ∈R,都有|ζ′(t)|≤C0. 若4α>p,我們可令 則ρ(t)∈C∞(R+,[0,1]),并且 最后,我們取 可得 考慮t ∈R+的情況,明顯有 可……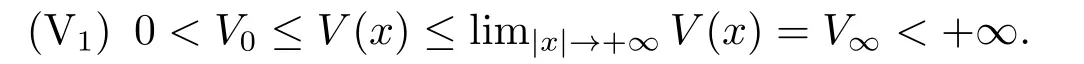
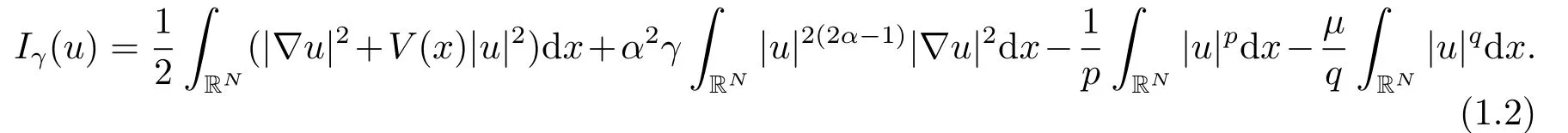
2.變量代換