談古代數學文化與現代數學的優美結合

☉河南省焦作市職業技術學校 劉艷群

2017年新課標高考考綱明確指出：增加考查我國古代數學文化與現代高考的優美結合.顯然，考綱這樣處理，有利于拓寬考生的知識面，凸顯古代數學文化的輝煌成果；有利于考查考生的閱讀理解能力和應用能力；有利于培養考生的創新精神，提高考生的數學素養.基于此，請賞析以下有關我國古代數學文化與現代數學的優美結合題.

類型一、我國古代數學文化與數列的優美結合

1.與等差數列優美結合

例1 在我國古代著名的數學專著《九章算術》里有一段敘述：今有良馬與駑馬發長安至齊，齊去長安一千一百二十五里，良馬初日行一百零三里，日增十三里；駑馬初日行九十七里，日減半里；良馬先至齊，復還迎駑馬，二馬相逢，問：幾日相逢？（ ）.

A.9日 B.8日 C.16日 D.12日

解析：由題意知，良馬每日行的距離構成等差數列，記為{an}，其首項a1=103，公差d=13；駑馬每日行的距離也構成等差數列，記為{bn}，其首項b1=97，公差d′=-0.5.

設兩馬經過m日相逢，則依據題意可得：

評注：本題需要先讀懂簡單的古文知識，將具體的實際問題轉化為熟悉的等差數列問題；然后借助等差數列的求和公式加以求解.

2.與等比數列優美結合

例2《九章算術》是我國古代的數學名著，其中有如下問題：“今有女子善織，日自倍，五日織五尺.問日織幾何？”意思是：“一女子善于織布，每天織的布都是前一天的2倍，已知她5天共織了5尺布，問：該女子每天分別織布多少？”據此分析，若織布的總尺數大于或等于30尺，則該女子至少需要（ ）天.

解析：設該女子第一天織布x尺，則根據題意可得≥30，得2n≥187，故n的最小值為8.故選B.

評注：對于本題，需要先讀懂題意，將具體的實際問題轉化為熟悉的等比數列問題；然后借助等比數列的求和公式靈活處理.

3.以數表為載體，與多個等差數列優美結合

例3 下面的數表為“森德拉姆篩”（森德拉姆，東印度學者），其特點是每行每列都成等差數列.

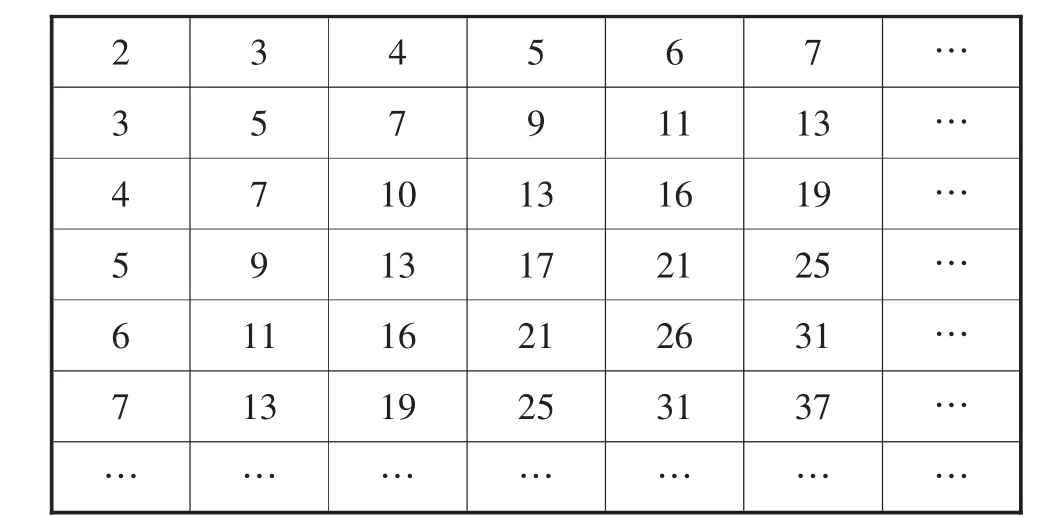
2 3 4 5 6 7 …3 5 7 9 11 13 …4 7 10 13 16 19 …5 9 13 17 21 25 …6 11 16 21 26 31 …7 13 19 25 31 37 ……………………

在上表中，101出現的次數為______.

解析：記第i行第j列的數為aij，那么每一組i與j的解就對應表中的一個數.

因為第1行的數組成的數列{a1j}（j=1，2，3，…）是以2為首項，1為公差的等差數列，所以a1j=2+（j-1）×1=j+1；

又第j列數組成的數列{aij}（i=1，2，3，…）是以j+1為首項，j為公差的等差數列，所以aij=j+1+（i-1）×j=ij+1.

令aij=101，則ij=100=1×100=2×50=4×25=5×20=10×10=20×5=25×4=50×2=100×1.

注意到因式1×100，可理解為101出現在數表的第1行第101列的位置，其他因式類似理解.

故101出現的次數為9.

評注：求解本題的關鍵點有兩個，一是兩次靈活運用等差數列的通項公式準確求得aij=ij+1；二是對數字100進行因式分解，要考慮全面.

類型二、我國古代數學文化與立體幾何的優美結合

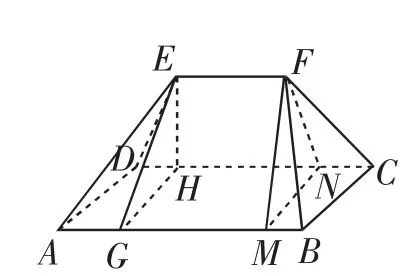
圖1

1.與割補法求體積優美結合

例4 我國古代數學名著《九章算術》卷五“商功”有如下問題：“今有芻甍，下廣三丈，袤四丈，上袤二丈，無廣，高一丈.問積幾何？”如圖1，可將其意思翻譯為：今有底面為矩形的屋脊形狀的多面體，其中AD=3丈，AB=4丈，EF=2丈，無寬，直線EF∥平面ABCD，且直線EF與平面ABCD的距離為1丈，那么該多面體的體積是多少？經計算，所求體積為（ ）.

A.4立方丈 B.5立方丈

C.6立方丈 D.8立方丈

解析：如圖1所示，過點E作底面ABCD的垂面EGH分別交AB，DC于點G，H，過點F作底面ABCD的垂面FMN分別交AB，DC于點M，N，則該多面體被分割為兩個全等的四棱錐E-DAGH，F-NMBC和一個直三棱柱EGH-FMN.

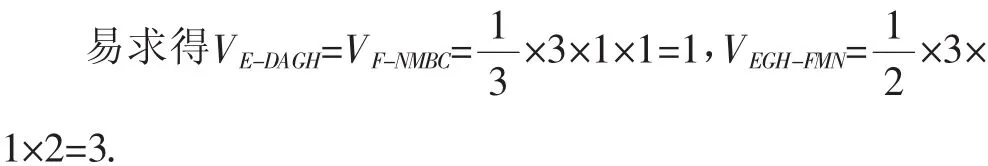
故該多面體的體積為1+1+3=5（立方丈）.故選B.

評注：結合圖形，理清題意之后，求解的關鍵點在于通過作截面，將所給的多面體分割成兩個四棱錐和一個直三棱柱，有利于借助“割補法”巧求體積.

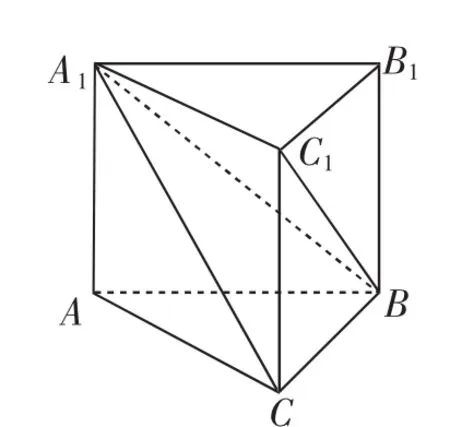
圖2

2.與特殊的幾何體優美結合

例5 我國古代數學名著《九章算術》中記載了有關特殊幾何體的定義：陽馬指底面為矩形，一側棱垂直于底面的四棱錐；鱉臑指四個面均為直角三角形的四面體；塹堵指底面為直角三角形，且側棱垂直于底面的三棱柱.如圖2，在塹堵ABC-A1B1C1中，AC⊥BC.

若A1A=AB=2，當陽馬B-A1ACC1的體積最大時：

①求塹堵ABC-A1B1C1的體積；

②求點C到平面A1BC1的距離；

③求二面角C-A1B-C1的余弦值.

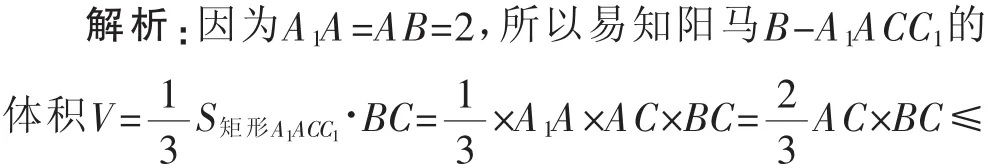
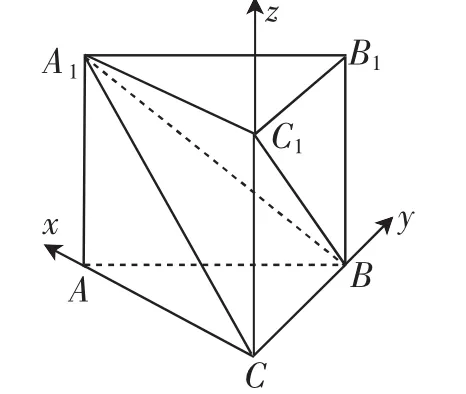
圖3

評注：本題易錯點：不能準確理解新名詞（塹堵、陽馬、鱉臑）的具體含義；不能將立體幾何中的有關概念、判定定理、性質定理及錐體的體積公式加以靈活運用.

綜上，求解此類問題時，需要先讀懂題意（很有必要熟悉簡單古文的翻譯），再靈活運用所學數學知識靈活處理.W