領悟數學思想 提高解題能力

歸明娟

(江蘇省蘇州工業園區星湖學校 215000)

在初中數學教學中，要幫助學生領悟正確的數學思想方法，以提高數學學習效率.如分類討論思想、數形結合思想、方程與函數思想、轉化與化歸思想等，這些也是歷年中考常見的考點，對此進行總結與分析有助提高學生的解題能力和技巧.

一、分類討論思想

分類討論思想即研究對象存在著一些不唯一現象或無法確定的因素，不能以統一的方法來描述，此時，要根據可能出現的各種結果進行分類研究，從而求出不同情況下的對應結論.進行分類時應遵循一定的原則：1.各分類情況間應彼此獨立；2.分類標準應統一；3.逐級展開分類討論.

例1 在一條數軸上分布有點A，B，C，其中點A表示的數為-4，點B表示的數為2，如果BC=3，那么AC等于( ).

A．9 B.5 C. 9或3 D. 3或8

分類討論：1.如果點C位于點B的右邊，那么點C表示的數為5，那么AC=5-(-4)=9；如果點C位于點B的左側，那么點C表示的數為-1，那么AC=-1-(-4)=3.所以，AC=9或3，所以正確答案是選項C.

點評當點與線段的位置存在無法確定的情況時，應對點在線段上的具體分布情況分類討論，才能正確、全面地解答相關問題.

二、數形結合思想

數形結合思想即借助幾何圖形研究代數數量關系，從而直觀、快速地解決代數問題，或借助代數數量關系解決幾何圖形問題，將代數與幾何巧妙地結合在一起，相輔相成，從而化繁為簡，化抽象為直觀，使數學問題得以巧妙解決的思想方法.

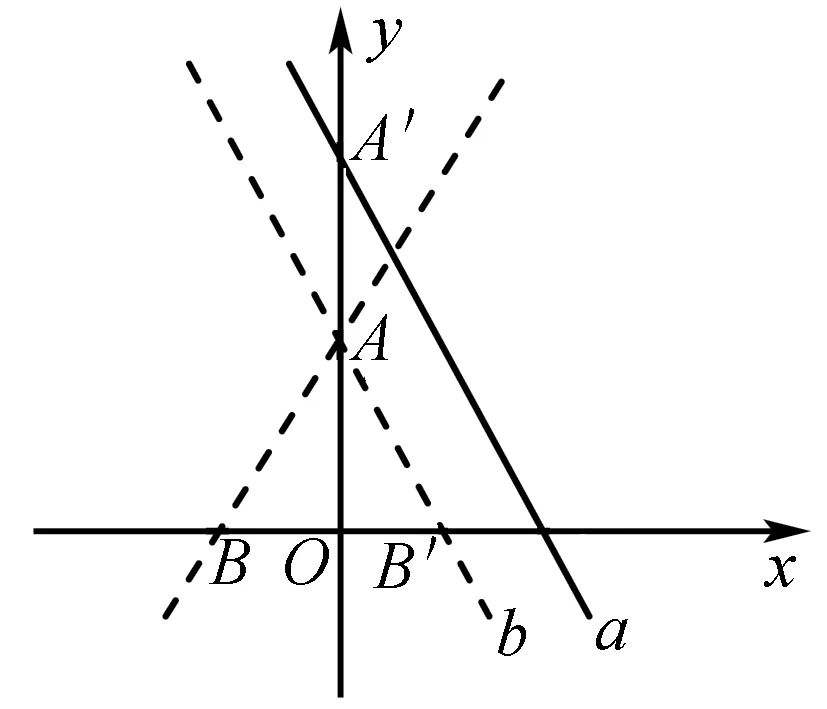
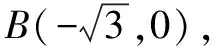
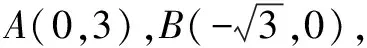
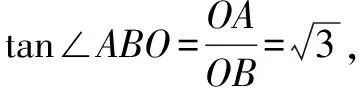
∴∠ABO=60°.由旋轉的性質得∠BAB′=60°，從而△ABB′為等邊三角形，

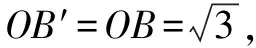
三、方程與函數思想

函數思想即借助函數的性質、函數圖象、函數概念等知識來分析、轉化和解決問題.方程思想即以所研究問題中的數量關系為切入點，運用數學語言將問題轉化為數學模型(方程、方程組、不等式、方程與不等式組合)，通過解方程(組)或不等式(組)來解決所研究的問題.有時，需要通過函數與方程間的相互轉化來解決問題.

例3 某商店出售一商品，已知商品的成本價是每千克20元，經過市場調查分析，此商品的每天銷量y(kg)與售價x(元/kg)有如下關系：y=-2x+80.如果該產品每天的銷售利潤為w元.

(1)試求w與x間的函數關系式；

(2)求此商品銷售價為多少時，商品每天銷售利潤才能實現最大化？并求出其最大利潤是多少；

(3)根據物價部門規定，此商品的售價不得高于每千克28元，如果要每天獲取150元的銷售利潤，銷售價應定為每千克多少元？

解(1)由題意，得w=(x-20)y=(x-20)(-2x+80)=-2x2+120x-1600.

故w與x的函數關系式為w=-2x2+120x-1600.

(2)w=-2x2+120x-1600=-2(x-30)2+200.

∵-2<0，∴當x=30時，w有最大值，最大值為200.

答：該產品銷售價定為每千克30元時，每天銷售利潤最大，最大銷售利潤為200元.

(3)當w=150時，可得方程-2(x-30)2+200=150.

解得x1=25,x2=35.∵35>28，∴x2=35與題意不符，正確答案應是每千克25元.

答：如果每天要想獲取150元的利潤，該商品的銷售價格應是每千克25元.

四、轉化與化歸思想

轉化與化歸思想是一種非常重要的數學思想，它的核心理念就是化未知為已知，化繁為簡，將陌生的、非常規的問題化為熟悉的、常規的問題，實現問題間的相互轉化，通過轉化找出問題的解答思路、方法，也就是將難題經過轉化后，變成有章可循，簡單易解的問題，從而順利解決問題的思想.

例4 如圖所示，有一菱形ABCD，其兩條對角線分別是AC，BD，且它們相交于點O，已知AC=8，BD=6，如果將AB作為直徑畫半圓，那么，圖中陰影部分的面積是( ).

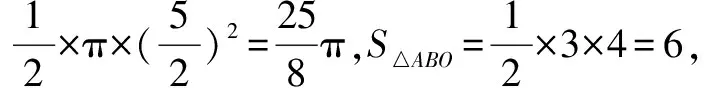
總結在數學問題解決中，遇到不規則圖形面積的求解時，需要將其轉化成規則圖形(圓形、扇形、三角形、四邊形等)，再利用規則圖形的概念、性質求出問題的解.